Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Градиент напряженности магнитного поля
|
|
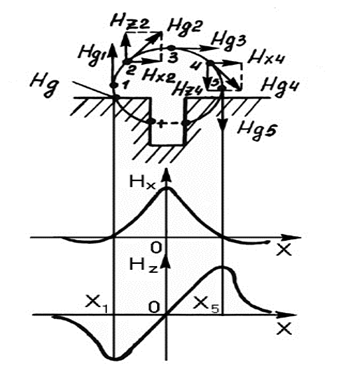Между точками х1 и х5 над дефектом, которые соответствуют экстремумам сигнала дефекта по Нz(х) (см. рис. 21), крутизна Нz(х) больше, чем в бездефектных зонах. Эта особенность может быть положена в основу метода магнитного контроля: измерять в каждой точке и сравнивать с порогом не значения функции Нz(х), а ее производной по координате х. Такая производная обозначается через Gz(х) и называется градиентом напряженности магнитного поля.
Представляется возможным, что, сравнивая функцию Нz(х) с некоторым фиксированным уровнем (порогом), можно безошибочно обнаружить дефект. в действительности же вне дефекта Нz(х) ≠ 0, а над дефектом Нz(х) значительно отличается от вида, представленного на рис. 22. Причинами этого можно назвать конечность размеров контролируемой детали, магнитные пятна, структурную неоднородность, резкие изменения сечения, шероховатость поверхности и др.
Реальная функция Нz(х) показана на рис. 22. Она представляет собой сумму Нz(х) сигнала дефекта (см. рис. 21) и случайной функции от названных выше причин, которую называют помехой. Помеха приводит к двум основным ошибкам дефектоскописта – пропуску (недобраковке) и ложному обнаружению дефекта (перебраковке). Очевидно, что невысокому значению отношения «сигнал/помеха» будет соответствовать большее количество ошибок.
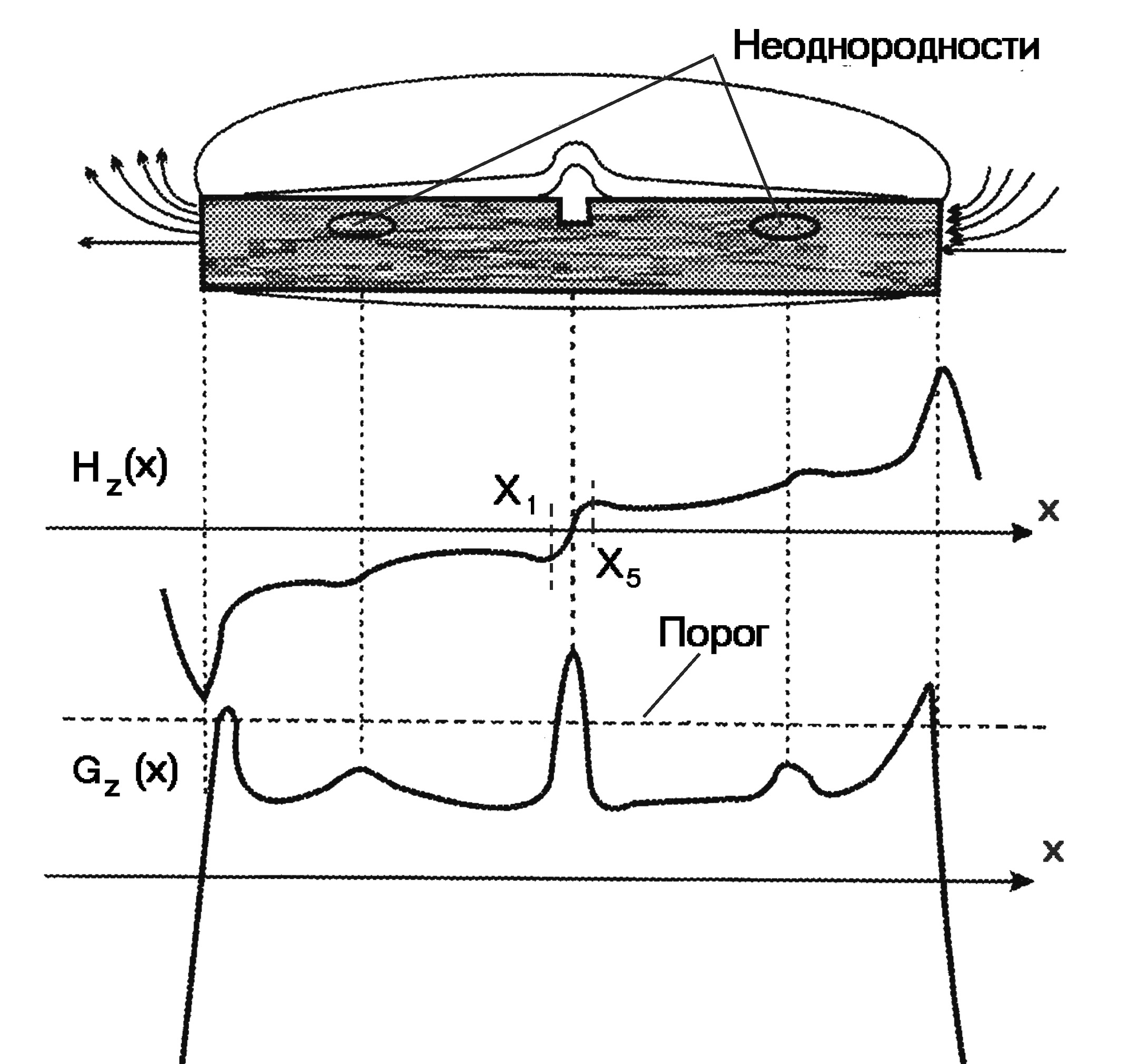
Рис. 22. Реальная функция градиента Hz(x)
На практике измерять градиент в виде производной сложнее и к тому же необязательно. Его величину оценивают как частное от деления разности значений напряженности в двух его соседних точках (последующей и предыдущей) в направлении намагничивания детали на расстояние между этими точками. Для однородных полей значение градиента равно нулю, для неоднородных – отлично от нуля. Различают градиенты по тангенциальной и нормальной составляющим, определяемым соответственно как
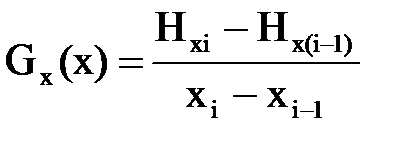и 
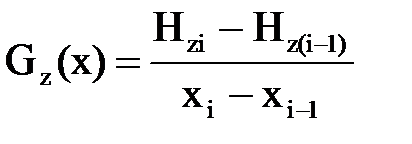. (32)
Например, по рис. 21 определим градиент нормальной составляющей поля дефекта в точке 2 (i = 2): 
Видно, что он будет отрицательным, так как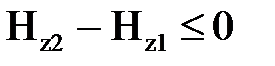 
, а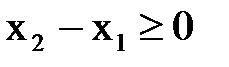 
. Следовательно, в направлении оси х нормальная составляющая поля убывает. Из рис. 22 видно, что дифференцирование дало существенное увеличение отношения «сигнал/помеха». В магнитной дефектоскопии используют градиент Gz(х), который более четко характеризует неоднородность магнитного поля рассеяния над дефектом.
Date: 2015-07-24; view: 3401; Нарушение авторских прав