
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Парная корреляция
|
|
Парная корреляция – это изучение корреляционной связи между двумя переменными.
Существуют несколько методов для исследования корреляционной связи между изучаемыми явлениями.
Одним из них является метод сопоставления параллельных рядов. Суть метода заключается в том, что значение факторного и результативного признаков располагают параллельными рядами, при этом значение факторного признака располагаются в порядке возрастания. Рассмотрим использование данного метода на примере 1.
Пример 1. Изучается зависимость производительности труда рабочих от продолжительности их работы на предприятии (стаж работы). Данные представлены в таблице 9.1.
Таблица 9.1 Исходные данные
| Табель- ный номер работ- ника | ||||||||||||
| Стаж работы (лет), x | ||||||||||||
| Произво- дитель- ность труда, (деталей в день), y |
В каждом ряду находится среднее значение факторного (x) и результативного признаков ( ). Они равны
). Они равны 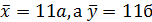 Затем находятся отклонение каждого значения x и y от средних значений. Если фактические значения x и y меньше среднего, то в таблице ставится минус, а если больше среднего, то знак ставится плюс. Проведем данные действия и полученные данные оформим в таблице 9.2.
Затем находятся отклонение каждого значения x и y от средних значений. Если фактические значения x и y меньше среднего, то в таблице ставится минус, а если больше среднего, то знак ставится плюс. Проведем данные действия и полученные данные оформим в таблице 9.2.
Таблица 9.2
| Номер работника | ||||||||||||
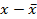
| - | - | - | - | - | - | + | + | + | + | + | + |
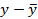
| - | - | - | - | - | + | - | + | + | + | + | + |
Из таблицы видно, что два раза знаки не совпали.
Для оценки тесноты взаимосвязи рассчитываются коэффициент Фехнера, который определяется по формуле:
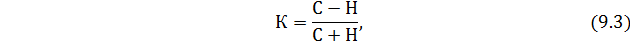
где С – число совпадений знаков,
Н – число несовпадений знаков.
Коэффициент принимает значение от-1 до +1, при отсутствии связи коэффициент равен 0.
Значение коэффициента будет равно:
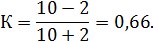
Это означает, что связь между изучаемыми признаками умеренная.
Преимущество данного метода – это простота вычислений, а недостаток: не всегда дает точные результаты.
Следующим методом изучения взаимосвязей между явлениями является метод аналитических группировок. Суть его состоит в том, что значения факторного признака группируются и по каждой группе находятся средние значения результативного признака. Рассмотрим использование данного метода на примере, приведенном выше.
Таблица 9.3
| Стаж работы (лет) | Количество работников, чел. | Средняя производительность труда, деталей в день |
| 1-6 6-12 12-18 18-24 | 177,5 183,6 |
Таким образом, расчеты показали, что с увеличением стажа работы рабочих увеличивается их производительность труда. Метод также является довольно простым, но не дает количественной оценки взаимосвязи.
Графический метод используется для предварительного анализа и оценок и дает наглядное представление о существующей связи между используемыми признаками. Данный метод заключается в том, что строится график, называемый полем корреляции.
Поле корреляции – это поле, на котором каждая точка соответствует единице совокупности, ее координаты определяются значениями признаков x и y. По характеру расположения точки на поле корреляции делают вывод о наличии или отсутствии связи, о характере связи (линейная или нелинейная), о направлении связи (прямая или обратная).
На рис. 9.1 представлены основные типы корреляции между двумя переменными.
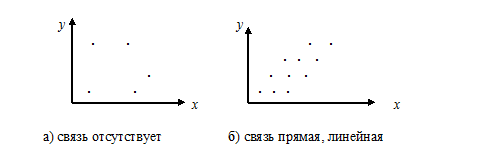
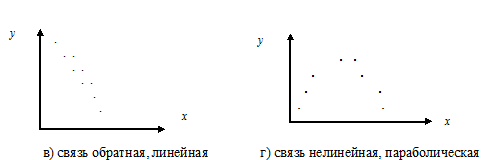

Рис. 9.1 Основные типы корреляции
Date: 2015-07-24; view: 939; Нарушение авторских прав