
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Прямолинейная зависимость
|
|
Если с помощью графического метода установлено, что точки колеблются вокруг прямой линии, то уравнение однофакторной линейной зависимости имеет вид:
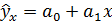 , (9.4)
, (9.4)
где 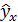 - теоретические значения результатов признака, полученные по
- теоретические значения результатов признака, полученные по
уравнению регрессии,
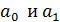 - коэффициенты (параметры) уравнения регрессии.
- коэффициенты (параметры) уравнения регрессии.
Параметр 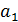 показывает насколько в среднем изменяется результативный признак, если факторный признак изменится на одну единицу.
показывает насколько в среднем изменяется результативный признак, если факторный признак изменится на одну единицу.
Параметр 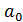 показывает, чему был равен результативный признак, если факторный признак принять за ноль.
показывает, чему был равен результативный признак, если факторный признак принять за ноль.
Параметры 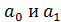 находятся методом наименьших квадратов:
находятся методом наименьших квадратов:
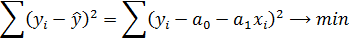
Для нахождения 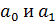 решается система двух линейных уравнений:
решается система двух линейных уравнений:
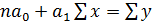
(9.5)
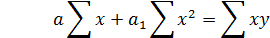
Определив значение 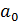 и
и 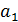 и подставив их в уравнение (9.5) находятся значения зависимости только от заданного значения x.
и подставив их в уравнение (9.5) находятся значения зависимости только от заданного значения x.
Для оценки тесноты взаимосвязи между факторным и результативными признаками рассчитывается коэффициент корреляции, который определяется по формуле:

Коэффициент корреляции находится в пределах от -1 до 1. При 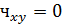 , связь отсутствует. Если
, связь отсутствует. Если 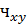 принимает значения 0-0,3 связь считается слабой, 0,31-0,5, связь умеренная, 0,51-0,7 связь заметная, а если xy оказывается >0,7 связь сильная. При обратной связи коэффициент имеет знак «минус».
принимает значения 0-0,3 связь считается слабой, 0,31-0,5, связь умеренная, 0,51-0,7 связь заметная, а если xy оказывается >0,7 связь сильная. При обратной связи коэффициент имеет знак «минус».
Квадрат коэффициента корреляции представляет собой коэффициент детерминации более предпочтительнее для измерения связи, так как он может быть использован для измерения не только линейных, но и нелинейных связей. Он может быть выражен в процентах и принимает значение в интервале от 0 до 1. Чем ближе к единице, тем теснее связь и наоборот.
Рассмотрим применение корреляционно-регрессионного анализа на примере изучения влияния стажа работы на производительность труда работников (исходные данные взяты из таблицы 9.1).
Вначале с целью определения формы связи строится поле корреляции (рис. 9.2).
| Производительность труда |
| Стаж работы |
| x |
| y |
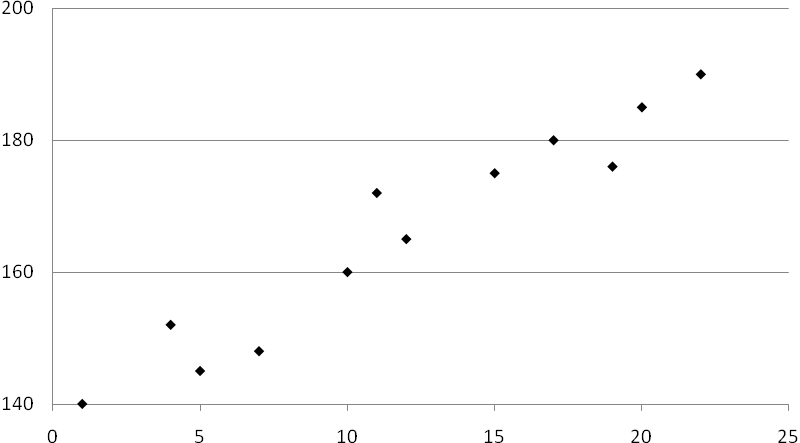
Рис. 9.2 Взаимосвязь между длительностью стажа и производительностью
труда работников
Из рисунка видно, что точки расположились кучно от левой части к его правой верхней части, это говорит о том, что связь между изучаемыми признаками существует, а по формуле она линейная. Аналитическую зависимость между рассматриваемыми признаками можно выразить уравнением прямой линии:
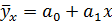
Найти параметр 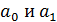 можно определить из системы уравнений (9.4). А для решения данной системы применяется способ определителей, позволяющий сводить к минимуму неточности определений в расчетах параметров уравнений регрессии.
можно определить из системы уравнений (9.4). А для решения данной системы применяется способ определителей, позволяющий сводить к минимуму неточности определений в расчетах параметров уравнений регрессии.
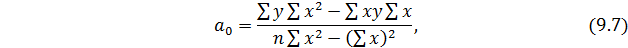
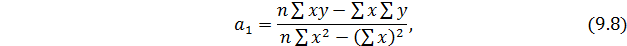
Для определения 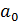 и
и 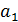 составляется расчетная таблица 9.4.
составляется расчетная таблица 9.4.
Таблица 9.4 Расчетная таблица
| Стаж работы, x | Производительность труда, y | 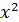
| xy | 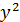
| 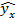
|
| 146,9 149,2 153,8 160,7 165,3 172,2 176,8 181,4 183,7 188,3 | |||||
| Итого: |
По итоговым данным таблицы определяются параметры уравнения регрессии:
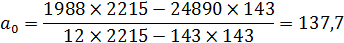
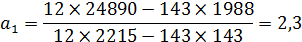
Таким образом, уравнение регрессии принимает вид:
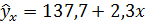
Параметры показывают: 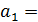 2, говорит, что при увеличении стажа работников на 1 год, производительность труда в среднем увеличивается на 2 детали в смену. Если принять стаж работы за ноль, а учитывать влияние других факторов производительность труда в смену составит 138 деталей.
2, говорит, что при увеличении стажа работников на 1 год, производительность труда в среднем увеличивается на 2 детали в смену. Если принять стаж работы за ноль, а учитывать влияние других факторов производительность труда в смену составит 138 деталей.
Коэффициент корреляции, определяемый по формуле (9.5), составит:
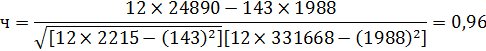
Коэффициент корреляции показывает, что взаимосвязь между признаками сильная.
Для нахождения теоретических значений результативного признака в полученное уравнение регрессии вместо x подставляется значение факторного признака (стаж работы).
Полученные значения 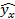 записываются в таблице 9.4, а на рис.9.3 изображены фактическая и теоретическая линии.
записываются в таблице 9.4, а на рис.9.3 изображены фактическая и теоретическая линии.
| x |
| Теоретическая линия |
| Фактическая линия |
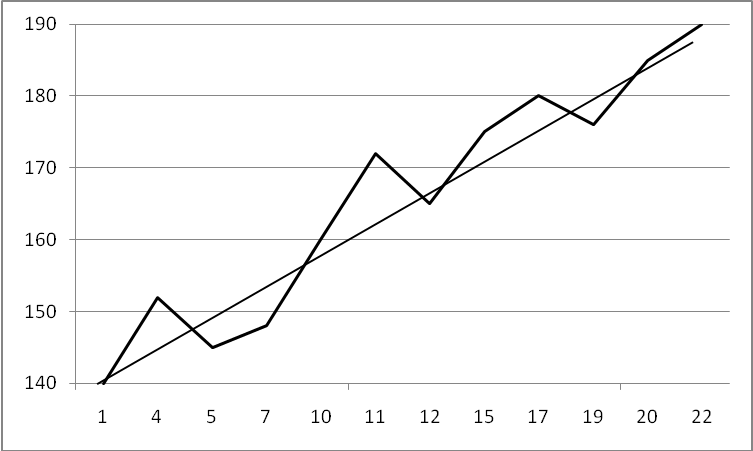
| y |
Рис. 9.3 Фактическая и теоретическая линия
Date: 2015-07-24; view: 662; Нарушение авторских прав