Катушки и конденсатора
На рис. 3.12 представлена схема параллельного соединения реальной индуктивной катушки с параметрами LК, RК и идеального конденсатора с емкостью С.
Для действующих комплексных значений токов на основании первого закона Кирхгофа запишем:
 

где активная и реактивные составляющие проводимостей находятся:
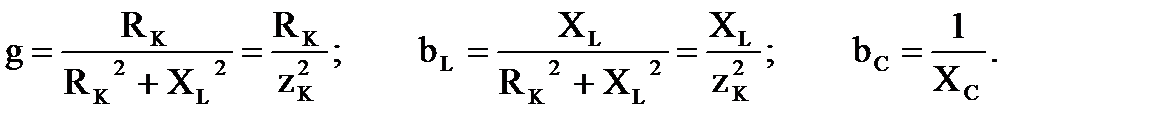
Ток реальной индуктивной катушки представлен как сумма активной составляющей, совпадающей по фазе с напряжением, и реактивной составляющей отстающей от напряжения по фазе на угол 90º:
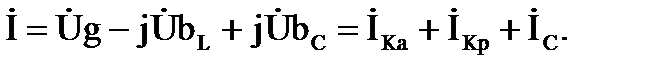
В этом случае на схеме замещения реальную индуктивную катушку можно представить в виде параллельного соединения двух ветвей с активной и реактивной проводимостями (рис. 3.13).
Заметим, что в случае, если ветвь содержит не один, а несколько элементов, активная и реактивная составляющие полной проводимости такой ветви будут определяться:
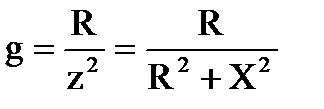 , , 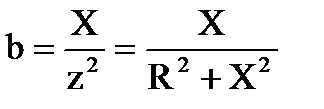 . .
Комплексная проводимость схемы рис. 3.12
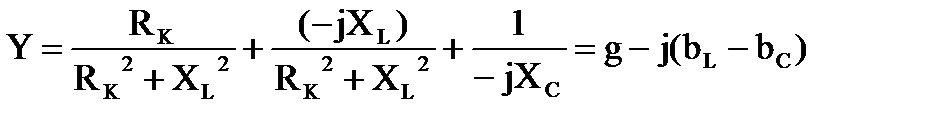 . .
Векторная диаграмма токов и напряжений (рис. 3.14) будет аналогична векторной диаграмме параллельного соединения идеальных элементов R, L, C.
Схемы замещения реальной индуктивной катушки и конденсатора
С помощью идеальных элементов R, L, C можно составить схемы замещения реальных элементов.
Так, катушка индуктивности с током IК, напряжением UК и углом сдвига фаз между ними φК на схеме замещения может быть представлена в виде последовательного (рис. 3.15, а) или параллельного (рис. 3.15, б) соединений активного и индуктивного элементов. Векторные диаграммы токов и напряжений для этих схем проведены соответственно на рис 3.16, а и б.
φK 
| Параметры схем замещения определяются следующим образом.
Для последовательной цепи:
Активная и реактивная составляющие напряжения и сопротивления катушки
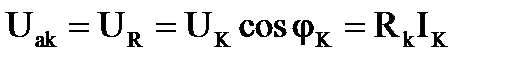 , тогда , тогда 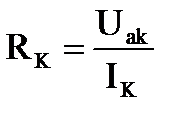 ; ;
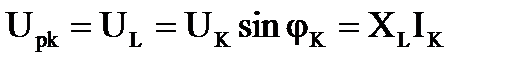 , тогда , тогда 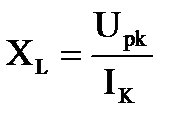 . .
Для параллельной цепи:
Активная и реактивная составляющие тока и проводимости катушки
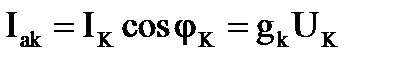 , тогда , тогда 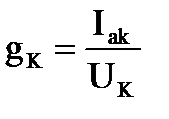 , ,
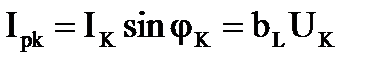 , тогда , тогда 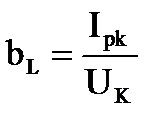 . .
При этом параметры последовательной и параллельной схем замещения связаны соотношениями
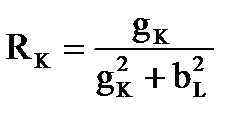 , , 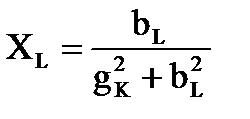 , ,
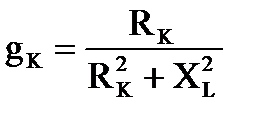 , , 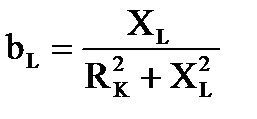 . .
Конденсатор с потерями в диэлектрике с током IКОН, напряжением UКОН и углом сдвига фаз между ними φкон на схеме замещения может быть представлена в виде последовательного (рис. 3.17, а) или параллельного (рис. 3.17, б) соединений активного и емкостного элементов.
Векторные диаграммы токов и напряжений для этих схем проведены соответственно на рис 3.18, а и б.
Параметры схем замещения определяются следующим образом.
Для последовательной цепи:
Активная и реактивная составляющие напряжения и сопротивления конденсатора
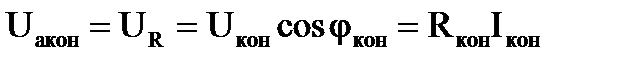 , тогда , тогда  ; ;
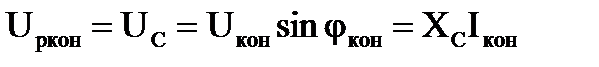 , тогда , тогда 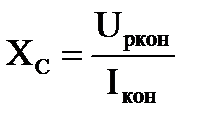 . .
Для параллельной цепи:
Активная и реактивная составляющие тока и проводимости конденсатора
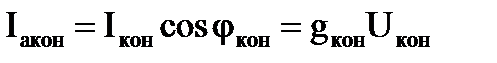 , тогда , тогда 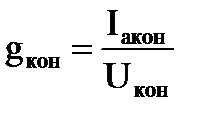 , ,
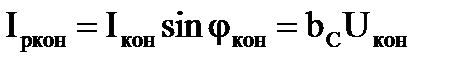 , тогда , тогда 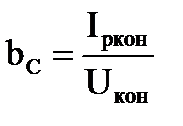 . .
При этом параметры последовательной и параллельной схем замещения связаны соотношениями
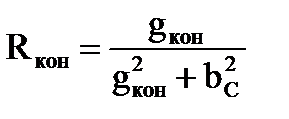 , , 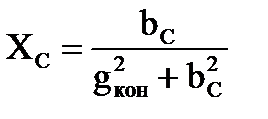 , ,
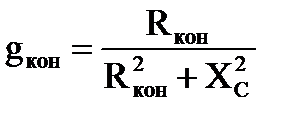 , , 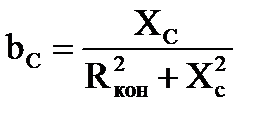 . .
Date: 2015-07-24; view: 564; Нарушение авторских прав | Понравилась страница? Лайкни для друзей: |
|
|






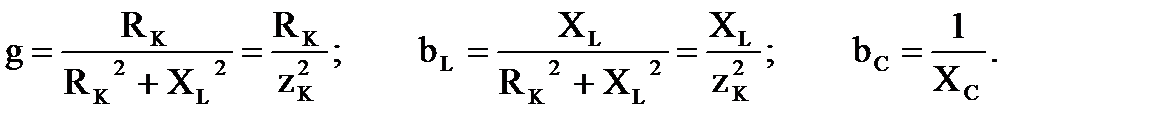
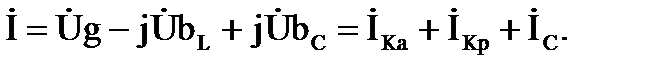
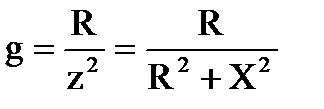 ,
, 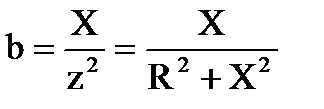 .
.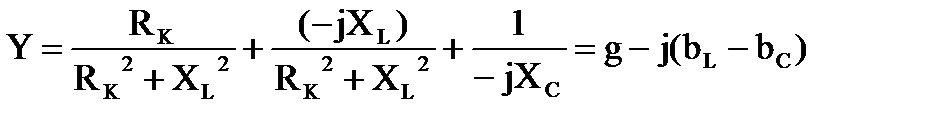 .
.
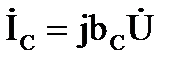
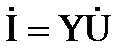
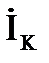
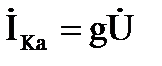
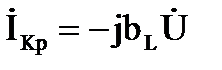
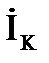
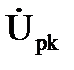
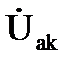
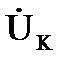
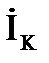
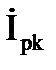
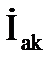
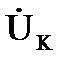
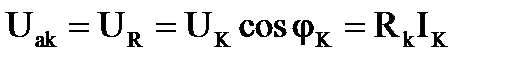 , тогда
, тогда 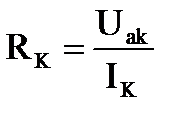 ;
;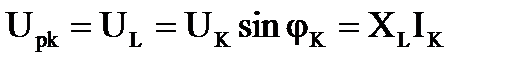 , тогда
, тогда 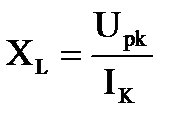 .
.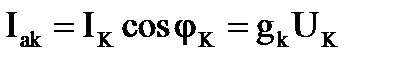 , тогда
, тогда 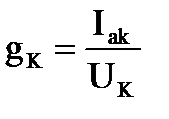 ,
,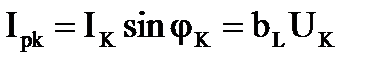 , тогда
, тогда 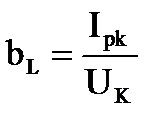 .
.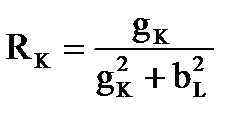 ,
, 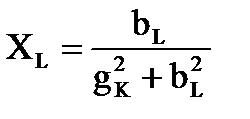 ,
,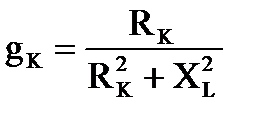 ,
, 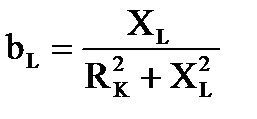 .
.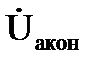
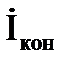
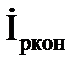
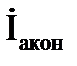
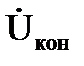
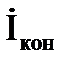
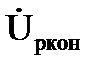
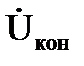
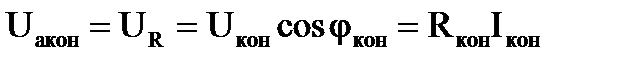 , тогда
, тогда  ;
;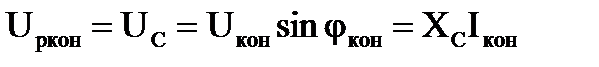 , тогда
, тогда 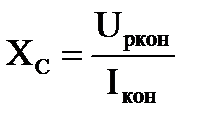 .
.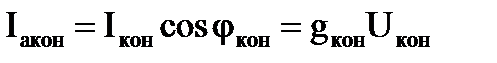 , тогда
, тогда 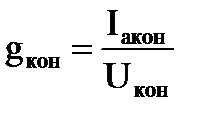 ,
,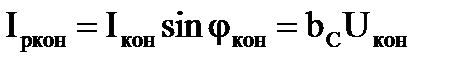 , тогда
, тогда 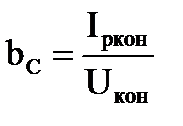 .
.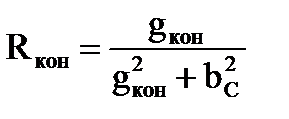 ,
, 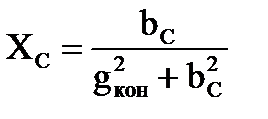 ,
,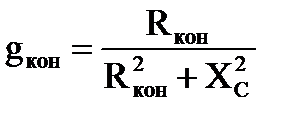 ,
, 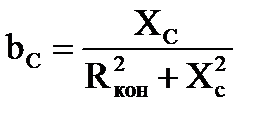 .
.