
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Линейные элементы R, L, C в цепи синусоидального тока
|
|
Лабораторная работа № 3
ИССЛЕДОВАНИЕ РЕЖИМОВ РАБОТЫ ЦЕПЕЙ
Синусоидального ТОКА
Цель работы: экспериментальное определение параметров пассивных элементов электрической цепи; исследование свойств электрической цепи с последовательным и параллельным соединением R, L, C элементов; получение навыков построения векторных диаграмм по опытным данным.
Теоретические сведения
Синусоидальный ток. Основные понятия
Мгновенные значения синусоидальных тока и напряжения определяются выражениями
i(t)= Im sin(ωt + ψi), u(t)= Um sin(ωt + ψu),
где Im, Um – амплитудные значения тока и напряжения;
(ωt + ψ) – фаза колебания, аргумент синусоидальной функции;
ω [рад/с] – угловая частота, которая может быть определена как ω =2πf = 2π/T;
f [Гц] – линейная частота; Т [c] – период колебаний;
ψi , ψu - начальные фазы тока и напряжения, которые отсчитываются от начала координат до ближайшей точки на оси абсцисс перехода синусоидальной функции через ноль от отрицательных к положительным ее значениям. Начальная фаза может быть положительной, отрицательной и равной нулю. При ψ>0 начало синусоиды сдвинуто влево относительно начала координат, при ψ < 0 – вправо, а при ψ = 0 синусоида имеет начало в начале координат.
На рис. 3.1 построены временные графики мгновенных значений тока и напряжения одинаковой частоты:
i(t)= Im sin(ωt + ψi), u(t)= Um sin(ωt + ψu).
Угол, на который синусоида тока сдвинута относительно синусоиды напряжения, называют углом сдвига фаз φ и определяют как разность начальных фаз напряжения и тока:
φ = ψu – ψi.

| φ |
| ψu |
| ψi |
| i,u |
| i(t) |
| u(t) |
| Im |
| Um |
| ωt |
Рис. 3.1
Большинство измерительных приборов измеряют действующие значения токов и напряжений. Поэтому расчеты в цепях синусоидального тока чаще всего выполняются по действующим значениям, которые связаны с амплитудными следующими соотношениями:  ,
, 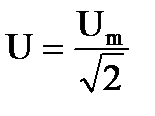 .
.
Линейные элементы R, L, C в цепи синусоидального тока
| R |
| uR(t) |
| i(t) |
При синусоидальном токе, протекающем по резистивному элементу i(t)= Imsin(ωt + ψi), напряжение на его зажимах и ток связаны законом Ома:
uR (t) = R i(t)= R Im sin(ωt + ψi) = URm sin(ωt + ψu).
Амплитудные и действующие значения тока и напряжения на резистивном элементе также связаны законом Ома:
URm = RIm, UR = RI.
| ψi |
| i,u |
| ωt |
| i |
| uR |
| pu |
| а) |
| ψi=ψu |
| +j |
| +1 |
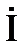
|
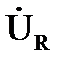
|
| б) |
| Рис. 3.2 |
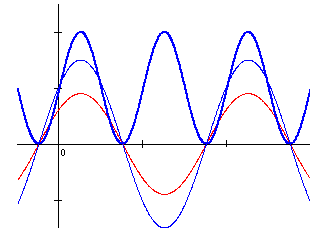
Из полученного выражения для мгновенного значения напряжения видно, что начальные фазы напряжения и тока одинаковы, то есть напряжение и ток резистивного элемента совпадают по фазе. На рис. 3.2, а представлены временные диаграммы тока и напряжения. При построении временных диаграмм начальная фаза тока принята положительной, ψi > 0.
Если синусоидальную функцию времени i(t)=Im sin(ωt+ψi) заменить изображающей ее комплексной величиной, то закон Ома в комплексной форме запишется следующим образом:
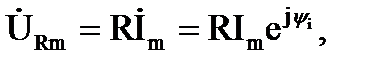
где 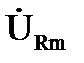 ,
, 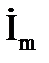 - комплексные амплитуды.
- комплексные амплитуды.
Или для действующих комплексных величин
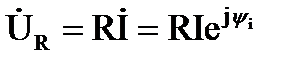 .
.
Векторы, изображающие синусоидальные функции времени, представлены на векторной диаграмме рис. 3.2, б.
Мгновенная мощность резистивного элемента
p(t) = uR·i = URm sin(ωt + ψu)·Im sin(ωt + ψi) =
= URm Im sin2(ωt + ψi)= URm Im 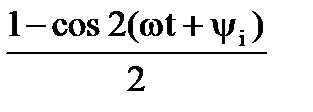 =
=
= 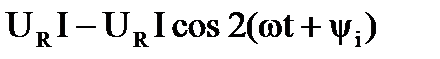 .
.
Временная диаграмма мгновенной мощности представлена на рис. 3.2, а. Из графика хорошо видно, что вся энергия, поступающая в резистивный элемент, расходуется в нем и не возвращается генератору.
Среднее значение мгновенной мощности за время, равное периоду синусоидального тока, называется активной мощностью:
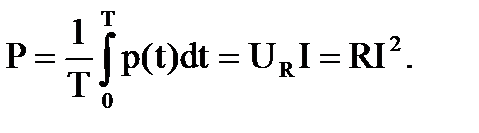
| uL(t) |
| i(t) |
| L |
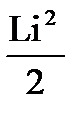 и явление самоиндукции. В этом случае пренебрегают потерями электромагнитной энергии и наличием энергии электрического поля.
и явление самоиндукции. В этом случае пренебрегают потерями электромагнитной энергии и наличием энергии электрического поля. Напряжение на зажимах индуктивного элемента при протекании синусоидального тока i(t)=Im sin(ωt + ψi) будет определяться:
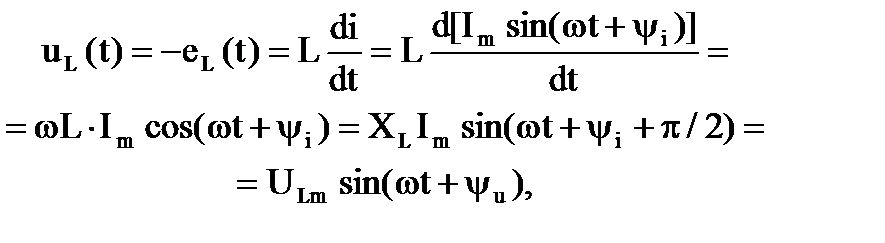
где 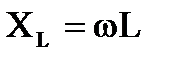 - индуктивное реактивное сопротивление синусоидальному току;
- индуктивное реактивное сопротивление синусоидальному току;
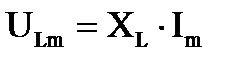 - амплитудное значение напряжения на индуктивном элементе;
- амплитудное значение напряжения на индуктивном элементе;
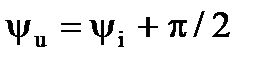 - начальная фаза напряжения, то есть напряжение на индуктивном элементе опережает свой ток на угол π/2.
- начальная фаза напряжения, то есть напряжение на индуктивном элементе опережает свой ток на угол π/2.
При переходе к действующим значениям имеем
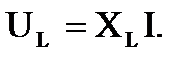
В комплексной форме записи:
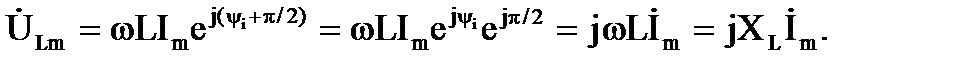
Для действующих комплексных значений
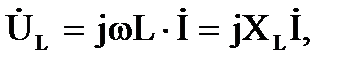
| φ |
| ψu |
| ψi |
| +j |
| +1 |
|
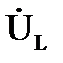
|
| π/2 |
| ψi |
| ψu |
| ωt |
| - |
| - |
| + |
| + |
| i, uL, p |
| uL(t) |
| i(t) |
| pL(t) |
| а) |
| б) |
| Рис. 3.3 |
здесь
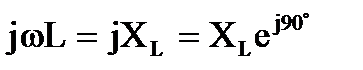 - индуктивное реактивное сопротивление в комплексной форме записи.
- индуктивное реактивное сопротивление в комплексной форме записи.
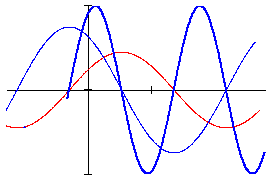
На рис. 3.3, а представлена временная диаграмма тока и напряжения индуктивного элемента. На рис. 3.3, б построена векторная диаграмма для действующих комплексных значений тока и напряжения.
Угол сдвига фаз φ на векторной диаграмме показывается стрелкой, направленной от вектора тока к вектору напряжения.
Мгновенная мощность индуктивного элемента может быть определена:
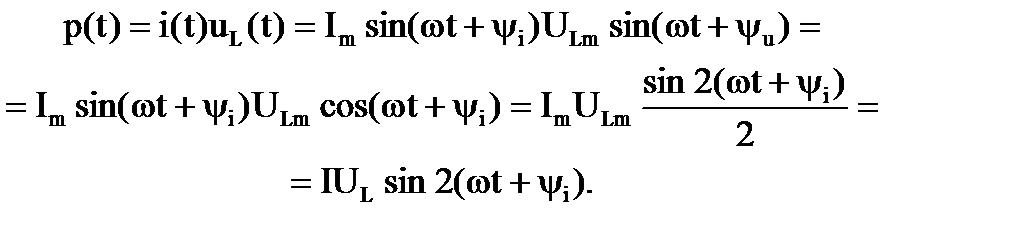
Как видно из полученного выражения, мгновенная мощность изменяется по синусоидальному закону с частотой в два раза больше, чем частота тока. График мгновенной мощности для индуктивного элемента представлен на рис. 3.3, а. Среднее значение мгновенной мощности за период равно нулю. В те промежутки времени, когда значение мгновенного тока увеличивается, мощность имеет положительное значение, энергия передается от генератора к индуктивному элементу и накапливается в нем. Когда же мгновенный ток уменьшается, мощность имеет отрицательное значение, энергия возвращается от индуктивного элемента к генератору. Для того чтобы количественно охарактеризовать обменные процессы магнитной энергией между источником и индуктивным элементом, вводят понятие индуктивной реактивной мощности, величина которой принимается равной амплитудному значению мгновенной мощности: 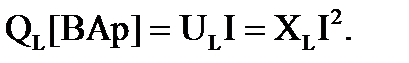
| uС(t) |
| i(t) |
| С |
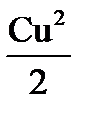 , пренебрегая при этом необратимым расходом энергии в диэлектрике и наличием энергии магнитного поля.
, пренебрегая при этом необратимым расходом энергии в диэлектрике и наличием энергии магнитного поля.
Ток ветви с конденсатором определяется:
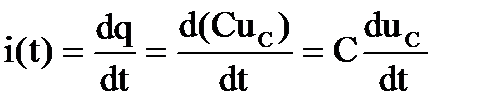 или
или
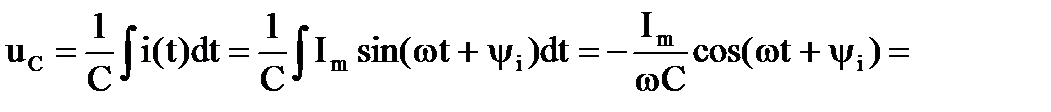
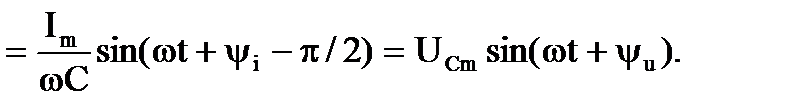
В приведенных выражениях: 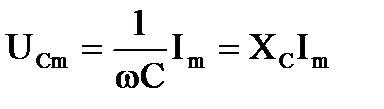 - амплитудное значение напряжения конденсатора;
- амплитудное значение напряжения конденсатора;
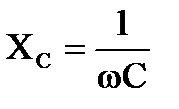 - реактивное емкостное сопротивление синусоидальному току;
- реактивное емкостное сопротивление синусоидальному току;
ψu=(ψi - π/2) – начальная фаза напряжения, то есть напряжение на емкостном элементе отстает от своего тока на угол π/2.
Для действующих значений: 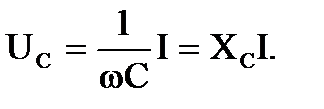
В комплексной форме записи:
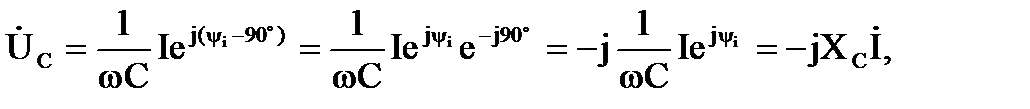
здесь 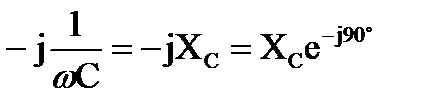 - реактивное емкостное сопротивление в комплексной форме записи.
- реактивное емкостное сопротивление в комплексной форме записи.
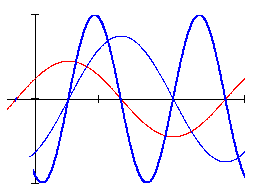
На рис. 3.4, а и б представлены временная и векторная диаграммы тока и напряжения емкостного элемента.
Мгновенная мощность емкостного элемента:
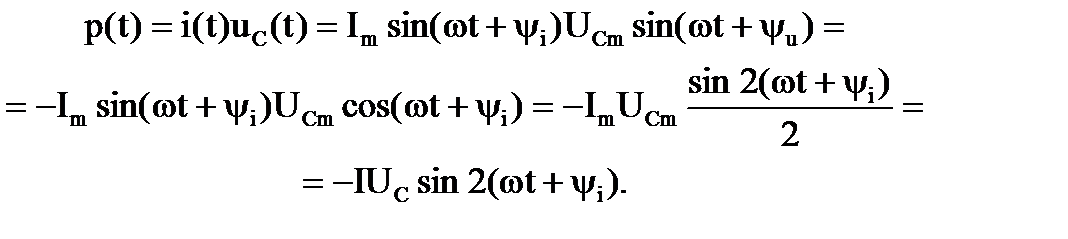 Временная диаграмма мгновенной мощности построена на рис. 3.4, а. Из графика мгновенной мощности следует, что среднее значение мощности за период также, как и у индуктивного элемента, равна нулю. В те промежутки времени, когда напряжение на емкостном элементе увеличивается, конденсатор заряжается, то есть энергия поступает от генератора к элементу (мощность положительна). В те промежутки времени, когда напряжение уменьшается, емкостный элемент возвращает генератору накопленную энергию (мощность от
Временная диаграмма мгновенной мощности построена на рис. 3.4, а. Из графика мгновенной мощности следует, что среднее значение мощности за период также, как и у индуктивного элемента, равна нулю. В те промежутки времени, когда напряжение на емкостном элементе увеличивается, конденсатор заряжается, то есть энергия поступает от генератора к элементу (мощность положительна). В те промежутки времени, когда напряжение уменьшается, емкостный элемент возвращает генератору накопленную энергию (мощность от
| φ |
| ψu |
| ψi |
| +j |
| +1 |
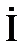
|
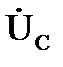
|
| -π/2 |
| ψi |
| ψu |
| i, uС, p |
| pС(t) |
| ωt |
| i(t) |
| uC(t) |
| - |
| + |
| + |
рицательна).
а) б)
Рис. 3.4
Для того чтобы количественно охарактеризовать эти обменные процессы, вводят понятие реактивной емкостной мощности, величина которой принимается равной амплитудному значению мгновенной мощности:
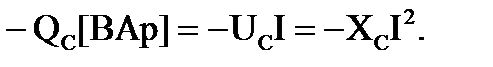
Как видно из временных диаграмм (рис. 3.3 и 3.4), в каждый момент времени индуктивная и емкостная мгновенные мощности находятся в противофазе. При расчете суммарной реактивной мощности значение индуктивной реактивной мощности берется положительным, а емкостной реактивной мощности - отрицательным.
Date: 2015-07-24; view: 1168; Нарушение авторских прав