Как извлечь корень из произвольного комплексного числа?

Рассмотрим уравнение 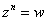, или, то же самое: 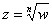. Здесь «эн» может принимать любое натуральное значение, которое больше единицы. В частности, при 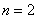получается квадратный корень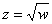

Уравнение вида 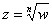имеет ровно 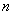корней 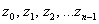, которые можно найти по формуле:
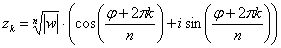, где 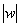– это модуль комплексного числа 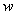, 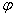– его аргумент, а параметр 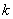принимает значения: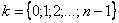

Пример 16

Найти корни уравнения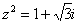

Перепишем уравнение в виде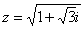

В данном примере 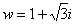, , 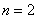поэтому уравнение будет иметь два корня: 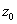и .
Общую формулу можно сразу немножко детализировать:
,

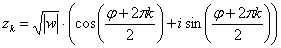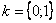
Теперь нужно найти модуль и аргумент комплексного числа :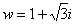

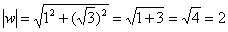
Число 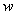располагается в первой четверти, поэтому:

Напоминаю, что при нахождении тригонометрической формы комплексного числа всегда желательно сделать чертеж.

Еще более детализируем формулу:
,

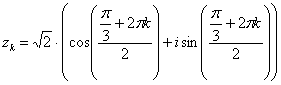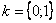
На чистовик так подробно оформлять, конечно, не нужно, это сделано мной для того, чтобы вам было понятно, откуда что взялось.

Подставляя в формулу значение 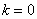, получаем первый корень:

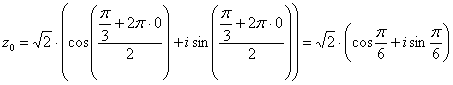
Подставляя в формулу значение 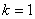, получаем второй корень:

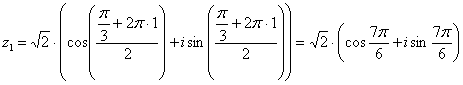
Ответ: ,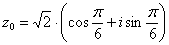

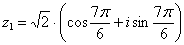
При желании или требовании задания, полученные корни можно перевести обратно в алгебраическую форму.

И напоследок рассмотрим задание - «хит», в контрольных работах почти всегда для решения предлагается уравнение третьей степени: .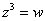

Пример 17

Найти корни уравнения 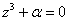, где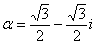

Сначала представим уравнение в виде :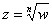

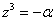
Если 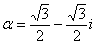, тогда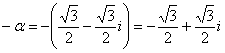

Обозначим 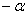привычной формульной буквой: .
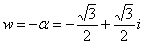Таким образом, требуется найти корни уравнения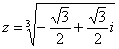

В данном примере 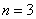, а значит, уравнение имеет ровно три корня: , ,
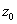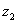
Детализирую общую формулу:
,

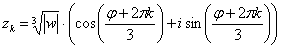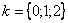
Найдем модуль и аргумент комплексного числа :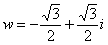

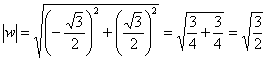
Число 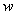располагается во второй четверти, поэтому:

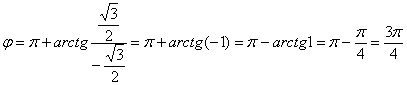
Еще раз детализирую формулу:
,
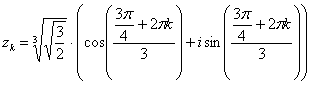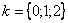
Корень удобно сразу же упростить:

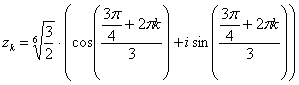
Подставляем в формулу значение 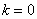и получаем первый корень:

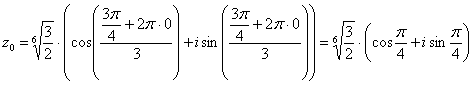
Подставляем в формулу значение 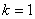и получаем второй корень:

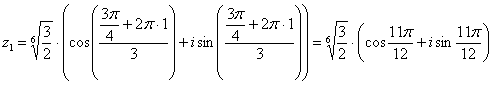
Подставляем в формулу значение 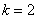и получаем третий корень:

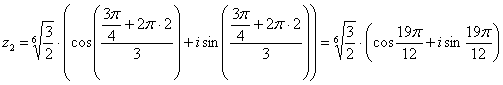
Очень часто полученные корни требуется изобразить геометрически:

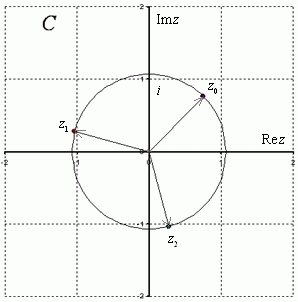
Как выполнить чертеж?
Сначала на калькуляторе находим, чему равен модуль корней 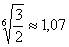и чертим циркулем окружность данного радиуса. Все корни будут располагаться на данной окружности.

Теперь берем аргумент первого корня 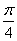и выясняем, чему равняется угол в градусах: 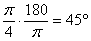. Отмеряем транспортиром 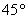и ставим на чертеже точку .

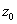Берем аргумент второго корня 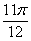и переводим его в градусы: 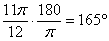. Отмеряем транспортиром 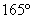и ставим на чертеже точку .

По такому же алгоритму строится точка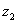

Легко заметить, что корни расположены геометрически правильно с интервалом 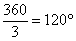между радиус-векторами. Чертеж крайне желательно выполнять с помощью транспортира. Если вы отмерите углы «на глазок», то рецензент легко это заметит и процентов 90-95 поставит минус за чертеж.

Уравнения четвертого 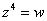и высших порядков встречается крайне редко, если честно, я даже не припомню случая, когда мне пришлось их решать. В этой связи ограничусь рассмотренными примерами.

Для чего нужны комплексные числа? Комплексные числа нужны для расширения сознания для выполнения заданий других разделов высшей математики, кроме того, они используются во вполне материальных инженерных расчетах на практике.

Желаю успехов!

Решения и ответы:

Пример 6: Решение:

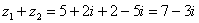
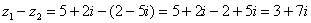
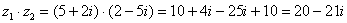
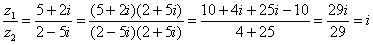
Пример 8: Решение:
Представим в тригонометрической форме число 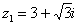. Найдем его модуль и аргумент. 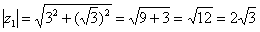. Поскольку 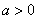(случай 1), то 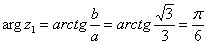. Таким образом: 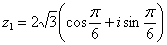– число в тригонометрической форме.

Представим в тригонометрической форме число 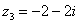. Найдем его модуль и аргумент. 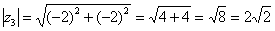. Поскольку 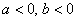(случай 3), то 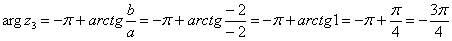. Таким образом: 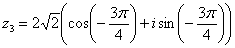– число 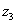в тригонометрической форме.

Пример 11: Решение: Представим число в тригонометрической форме: 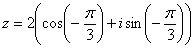(это число 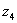Примера 8). Используем формулу Муавра :

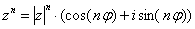Пример 13: Решение:

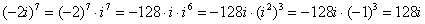
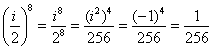
Пример 15: Решение:


,
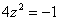
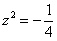
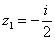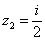
Разложим квадратный двучлен на множители:

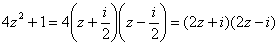
Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Date: 2015-07-23; view: 478; Нарушение авторских прав