Решение системы методом почленного сложения (вычитания) уравнений системы

В ходе решения систем линейных уравнений нужно стараться использовать не «школьный метод», а метод почленного сложения (вычитания) уравнений системы. Почему? Это экономит время и упрощает вычисления, впрочем, сейчас станет всё понятнее.

Пример 4

Решить систему линейных уравнений:

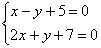
Я взял ту же систему, что и первом примере.
Анализируя систему уравнений, замечаем, что коэффициенты при переменной 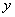одинаковы по модулю и противоположны по знаку (–1 и 1). В такой ситуации уравнения можно сложить почленно:

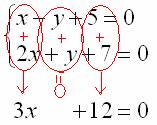
Действия, обведенные красным цветом, выполняются МЫСЛЕННО.
Как видите, в результате почленного сложения у нас пропала переменная 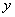. В этом, собственно, и состоит суть метода – избавиться от одной из переменных.

Теперь всё просто: 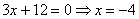– подставляем в первое уравнение системы (можно и во второе, но это не так выгодно – там числа больше):

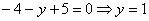
В чистовом оформлении решение должно выглядеть примерно так:

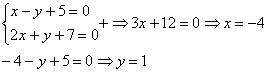
Ответ: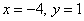

У некоторых явно возник вопрос: «Зачем все эти изыски, если можно просто выразить одну переменную через другую и подставить во второе уравнение?».

Пример 5

Решить систему линейных уравнений:

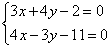
В данном примере можно использовать «школьный» метод, но большой минус состоит в том, что когда мы будем выражать какую-либо переменную из любого уравнения, то получим решение в обыкновенных дробях. А возня с дробями займет время, к тому же, если у Вас не «набита рука» на действиях с дробями, то велика вероятность допустить ошибку.

Поэтому целесообразно использовать почленное сложение (вычитание) уравнений. Анализируем коэффициенты при соответствующих переменных:

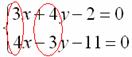
Как видим числа в парах (3 и 4), (4 и –3) – разные, поэтому, если сложить (вычесть) уравнения прямо сейчас, то от переменной мы не избавимся. Таким образом, хотелось бы видеть в одной из пар одинаковые по модулю числа, например, 20 и 20 либо 20 и –20.

Будем рассматривать коэффициенты при переменной :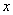

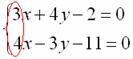
Подбираем такое число, которое делилось бы и на 3 и на 4, причем оно должно быть как можно меньше. В математике такое число называется наименьшим общим кратным. Если Вы затрудняетесь с подбором, то можно просто перемножить коэффициенты: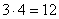

Далее:
Первое уравнение умножаем на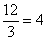
Второе уравнение умножаем на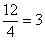

В результате:

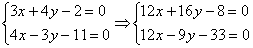
Вот теперь из первого уравнения почленно вычитаем второе. На всякий случай привожу еще раз действия, которые проводятся мысленно:

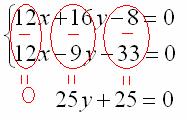
Следует отметить, что можно было бы наоборот – из второго уравнения вычесть первое, это ничего не меняет.

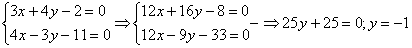
Теперь подставляем найденное значение 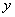в какое-нибудь из уравнений системы, например, в первое:

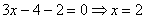
Ответ: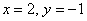

Решим систему другим способом. Рассмотрим коэффициенты при переменной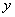

Очевидно, что вместо пары коэффициентов (4 и –3) нам нужно получить 12 и –12.
Для этого первое уравнение умножаем на 3, второе уравнение умножаем на 4:

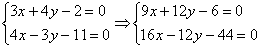
Почленно складываем уравнения и находим значения переменных:

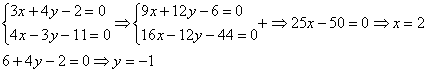
Ответ: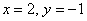

Второй способ несколько рациональнее, чем первый, так как складывать проще и приятнее чем вычитать.

Date: 2015-07-23; view: 578; Нарушение авторских прав