Решение системы линейных уравнений методом подстановки

Данный метод также можно назвать «школьным методом» или методом исключения неизвестных. Образно говоря, его еще можно назвать «недоделанным методом Гаусса».

Пример 1

Решить систему линейных уравнений:

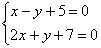
Здесь у нас дана система из двух уравнений с двумя неизвестными. Обратите внимание, что свободные члены (числа 5 и 7) расположены в левой части уравнения. Вообще говоря, без разницы, где они находятся, слева или справа, просто в задачах по высшей математике нередко они расположены именно так. И такая запись не должна приводить в замешательство, при необходимости систему всегда можно записать «как обычно»: 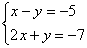. Не забываем, что при переносе слагаемого из части в часть у него нужно поменять знак.

Что значит решить систему линейных уравнений? Решить систему уравнений – это значит найти такие значения переменных, которые обращают КАЖДОЕ уравнение системы в верное равенство. Это утверждение справедливо для любых систем уравнений с любым количеством неизвестных.

Существует графический метод решения системы, с которым можно ознакомиться на уроке Простейшие задачи с прямой. Там же я рассказал о геометрическом смысле системы двух линейных уравнений с двумя неизвестными. Но сейчас на дворе эра алгебры, и числа-числа, действия-действия.

Решаем. Из первого уравнения выразим: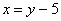
Полученное выражение 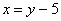подставляем во второе уравнение:

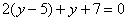
Раскрываем скобки, приводим подобные слагаемые и находим значение :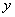

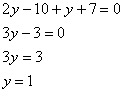
Далее вспоминаем про то, от чего плясали: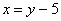
Значение 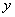нам уже известно, осталось найти: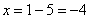

Ответ: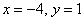

После того, как решена ЛЮБАЯ система уравнений ЛЮБЫМ способом, настоятельно рекомендую выполнить проверку на черновике или калькуляторе. Благо, делается это легко и быстро.

1) Подставляем найденный ответ 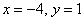в первое уравнение :

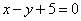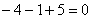
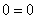– получено верное равенство.

2) Подставляем найденный ответ 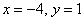во второе уравнение :

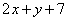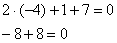
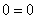– получено верное равенство.

Или, если говорить проще, «всё сошлось»

Рассмотренный способ решения не является единственным, из первого уравнения можно было выразить 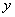, а не .
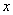Можно наоборот – что-нибудь выразить из второго уравнения 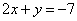и подставить в первое уравнение. Кстати, заметьте, самый невыгодный из четырех способов – выразить 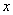из второго уравнения:

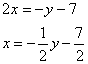
Получаются дроби, а оно зачем? Есть более рациональное решение.

Тем не менее, в ряде случаев без дробей всё-таки не обойтись. В этой связи обращаю Ваше вниманиена то, КАК я записал выражение. Не так: 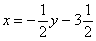, и ни в коем случае не так: .

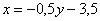Date: 2015-07-23; view: 492; Нарушение авторских прав