Матричные выражения

Повторим обычные школьные выражения с числами. Числовое выражение состоит из чисел, знаков математических действий и скобок, например: 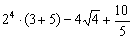. При расчётах справедлив знакомый алгебраический приоритет: сначала учитываются скобки, затем выполняется возведение в степень / извлечение корней, потом умножение / деление и в последнюю очередь – сложение /вычитание.

Если числовое выражение имеет смысл, то результат его вычисления является числом, например:

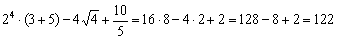
Матричные выражения устроены практически так же! С тем отличием, что главными действующими лицами выступают матрицы. Плюс некоторые специфические матричные операции, такие, как транспонирование и нахождение обратной матрицы.

Рассмотрим матричное выражени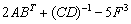е , где 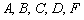– некоторые матрицы. В данном матричном выражении три слагаемых и операции сложения/вычитания выполняются в последнюю очередь.

В первом слагаемом 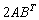сначала нужно транспонировать матрицу «бэ»: 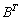, потом выполнить умножение 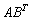и внести «двойку» в полученную матрицу. Обратите внимание, что операция транспонирования имеет более высокий приоритет, чем умножение. Скобки, как и в числовых выражениях, меняют порядок действий: 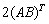– тут сначала выполняется умножение 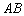, потом полученная матрица транспонируется и умножается на 2.

Во втором слагаемом 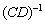в первую очередь выполняется матричное умножение 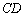, и обратная матрица находится уже от произведения. Если скобки убрать: 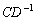, то сначала необходимо найти обратную матрицу 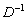, а затем перемножить матрицы: 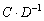. Нахождение обратной матрицы также имеет приоритет перед умножением.

С третьим слагаемым 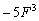всё очевидно: возводим матрицу в куб и вносим «пятёрку» в полученную матрицу.

Если матричное выражение имеет смысл, то результат его вычисления является матрицей.

Все задания будут из реальных контрольных работ, и мы начнём с самого простого:

Пример 9

Даны матрицы 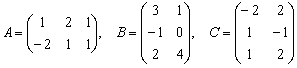. Найти:

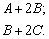
Решение:порядок действий очевиден, сначала выполняется умножение, затем сложение.

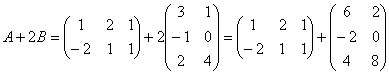
Сложение выполнить невозможно, поскольку матрицы разных размеров.

Не удивляйтесь, заведомо невозможные действия часто предлагаются в заданиях данного типа.

Пробуем вычислить второе выражение:

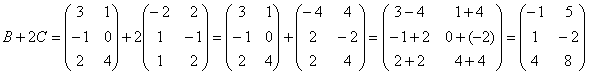
Тут всё нормально.

Ответ: действие 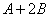выполнить невозможно, .

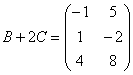Повысим градус:

Пример 10

Даны матрицы .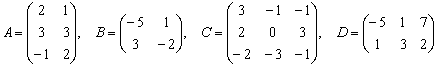

Найти значения выражений:

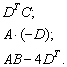
Решение: Разбираемся с произведением 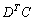. Сначала транспонируем матрицы «дэ»:

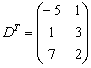
И умножаем матрицы:

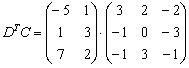
Матричное умножение выполнить невозможно, так как число столбцов матрицы 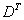не равно числу строк матрицы .

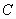А вот с произведением 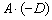проблем не возникает:

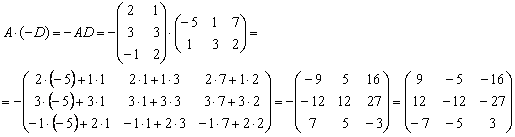
Еще раз заметьте, как на первом же шаге множитель (–1) выносится вперёд, и ноги до него доходят в самую последнюю очередь.

С более сложными выражениями вроде 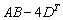чайникам рекомендую разбираться поэтапно, чтобы не запутаться:

Сначала находим произведение:

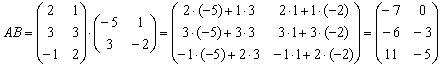
Затем считаем второе слагаемое:

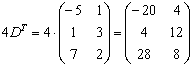
И, наконец, всё выражение:

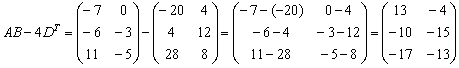
Более подготовленные студенты могут оформить решение одной строкой:

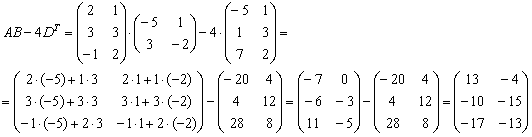
Ответ: действие 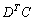выполнить невозможно, , .

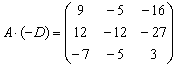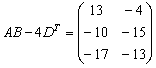Пара заключительных примеров для самостоятельного решения:

Пример 11

Для матриц Примера №10 выполнить действия:

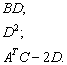
Пример 12

Вычислить значение матричного многочлена 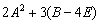, если .

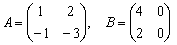В последнем примере решение удобно оформить по пунктам.

Матричные выражения – это просто! И вряд ли на практике вам встретится что-то сложнее, чем разобранные примеры.

Теперь во всеоружии можно приступить к изучению матричных уравнений.

Желаю успехов!

Решения и ответы:

Пример 2: Решение:

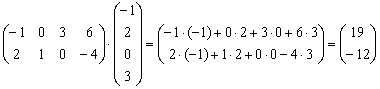
Ответ: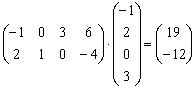

Пример 5: Решение:

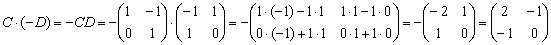
Ответ: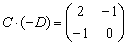

Пример 7: Решение:
1) Используем формулу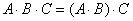

2) Используем формулу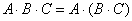

Ответ: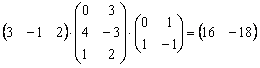

Пример 8: Решение: Сначала возведём матрицу в квадрат:

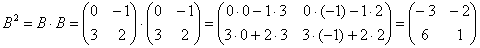
Возведём матрицу в куб:

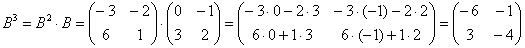
Возведём матрицу в четвёртую степень двумя способами:


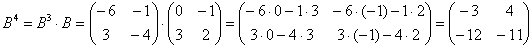
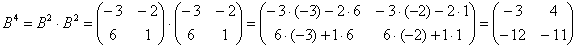
Ответ: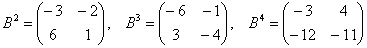

Пример 11: Решение:

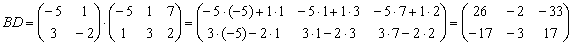
Возведение в квадрат 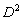невозможно, поскольку операция определена только для квадратных матриц.

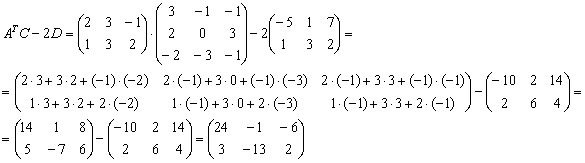
Ответ: 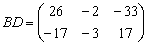, действие 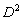выполнить невозможно,

Пример 12: Решение:
1)
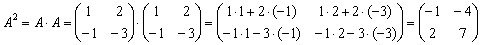
2)
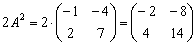
3)
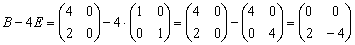
4)
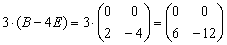
5)
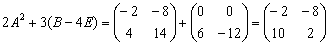
Ответ: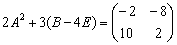
Примечание: выражение можно было вычислить и по-другому – предварительно раскрыть скобки: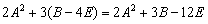

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Date: 2015-07-23; view: 4943; Нарушение авторских прав