Эстафета с использованием акробатических элементов

Игроки двух команд выстраиваются на ковре или двух дорожках из матов в колонны по одному с дистанцией 2 м. По сигналу, стоящие последними в командах, выполняют кувырок вперед и касаются рукой впереди стоящего игрока. Тот выполняет кувырок и передает эстафету дальше. Побеждает команда, быстрее справившаяся с заданием.

Эстафету можно проводить с выполнением кувырка назад, переворота боком. Важно при этом правильно рассчитать дистанцию между играющими.

ЧАСТЬ ТРЕТЬЯ. ОРГАНИЗАЦИЯ И МЕТОДИКА

ЗАНЯТИЙ ГИМНАСТИКОЙ

ГЛАВА 10. БИОМЕХАНИЧЕСКИЕ ОСНОВЫ ТЕХНИКИ

ГИМНАСТИЧЕСКИХ УПРАЖНЕНИЙ

10.1. Сохранение устойчивости тела в статических упражнениях

Техника гимнастических упражнений подчиняется закономерностям механики, в которой выделяются ее составные части: статика, кинематика, динамика. Виды и условия равновесий тел изучает статика. Принято выделять четыре вида статических равновесий: устойчивое, неустойчивое, ограниченно–устойчивое, безразличное. Принадлежность к конкретному виду равновесий определяется «поведением» тела при его отклонении от первоначального (базового) положения. Поясним сказанное рисунками, на которых каждый вид равновесия представлен механической (физической) моделью.

На рис. 173 показана модель устойчивого равновесия в виде маятника. Если маятник отклонить на некоторый угол ₤ из положения 1 в положение 2, а затем отпустить его, то после нескольких колебаний он обязательно остановится под действием момента силы тяжести, который называется моментом устойчивости: Му= РL, где Р – сила тяжести, L – плечо силы тяжести. То же произойдет с гимнастом, находящимся в висе на любом снаряде. Характерным признаком устойчивого равновесия является расположение центра масс тела ниже точки (площади) опоры.

Рис. 173

Моделью неустойчивого равновесия может служить стержень (столб) с очень малой площадью опоры, свободно стоящий на поверхности (рис. 174). При самом незначительном отклонении от вертикали произойдет падение (опрокидывание) тела под действием момента опрокидывания: Мо=РL.

Рис. 174

В качестве примера из гимнастической практики к неустойчивому равновесию можно отнести стойку на одной руке или стойку на полупальцах одной ноги. Характерным признаком неустойчивого равновесия является расположение общего центра масс тела (ОЦМ) выше площади опоры.

Третий вид равновесия называется ограниченно–устойчивым равновесием (ОУР). ОУР проявляется в упражнениях, когда гимнаст опирается на относительно большую площадь, находясь при этом выше опорной поверхности. К таким упражнениям относятся различные стойки на руках, на одной и двух ногах, на голове и руках, выполняемые на брусьях и кольцах, на полу и на партнере.

На рис. 175 показана механическая модель ОРУ. Проследим «поведение» предмета, свободно стоящего на ровной поверхности. В первоначальном (базовом) положении 1 предмет неподвижен, т.к. общий центр масс (его проекция) расположен в пределах площади опоры и все точки его основания касаются поверхности. В положении 2 ОЦМ предмета не вышел за пределы площади опоры и в случае прекращения воздействия (поворота, наклона в сторону), предмет вернется в положение 1. Причина возвращения – действие момента устойчивости: Му= РL₂, где Р – сила тяжести, L₂ – плечо силы.

Рис. 175

Если же наклонить предмет в положение 3 и отпустить поддержку, то произойдет падение (опрокидывание) предмета, благодаря действию момента опрокидывания: Мо= РL₃. Заметим, что ограниченно–устойчивое равновесие является управляемым равновесием – УР, т.к. гимнаст в известных пределах может самостоятельно ликвидировать начало падения за счет компенсаторных действий, суть которых сводится к тому, чтобы ОЦМ тела всегда находился в пределах площади опоры.

Наконец, существует так называемое безразличное равновесие, особенность которого состоит в том, что тело в случае его отклонения от начального положения остается в новом положении без изменения своего «поведения».

На рис. 176 показана модель безразличного равновесия в виде шара, находящегося в гладкой горизонтальной площадке. При откате шара из положения 1 в положение 2 и его остановке, шар останется в неподвижном состоянии, т.к. отсутствует побудительная причина для его движения по площадке, т.е. Мо=Му=О.

Рис. 176

Примером безразличного равновесия в гимнастике с определенной долей условности может служить спортсмен, находящийся в плотной группировке в положении лежа на полу.

Об устойчивости тела гимнаста

К статике гимнастических упражнений также относятся вопросы устойчивости тела при выполнении упражнений. Различают статическую и динамическую устойчивость. Первая из них характеризует способность тела противостоять нарушению равновесия, а вторая – способностью восстанавливать равновесие в случае его нарушения.

На рис. 177 изображена модель тела, на которой обозначены параметры статической устойчивости последнего: момент устойчивости Му=РL, опрокидывающий момент Мо=Fh, коэффициент устойчивости К= ^Му , углы

^Мо

устойчивости ₤₁ и ₤₂ , угол равновесия ₤₁+₤₂, угол равновесия ₤₁+₤₂, база устойчивости L. Совершенно очевидно, то степень устойчивости тела находится в прямой зависимости от величин указанных параметров: чем больше значение параметров, тем выше устойчивость и – наоборот.

Рис. 177

В качестве иллюстрации сказанному, покажем три различных статических положения, отличающихся друг от друга высотой расположения ОЦМ, площадью опоры, углами устойчивости и равновесия.

Рис. 178

На рис.178 схематично изображены три различные стойки: на руках, голове и руках, на груди. Нетрудно видеть, что наиболее устойчивым является положение в, т.к. здесь, по сравнению с положениями а и б, параметры устойчивости тела – углы устойчивости и равновесия, а также база устойчивости – более значительны. Вместе с тем устойчивость и высота расположения ОЦМ тела находятся в обратной зависимости: чем ниже ОЦМ, тем выше устойчивость.

10.2. Сохранение устойчивости тела в динамических упражнениях

Динамическая устойчивость реализуется в динамическом равновесии, т.е. в случаях, когда необходимо удержать равновесие в движении. Это можно показать на примере размахивания в упоре на брусьях (рис.179). Положение 1 на рисунке соответствует крайней точке маха вперед, при котором гимнаст отводит плечи назад для компенсации возникающего опрокидывающего момента силы тяжести: Мо₁=Рτ₁. В положении 2 гимнаст достигает крайней точки маха назад и соответственно «подает» плечи вперед для противодействия опрокидывающему моменту: Мо₂=Рτ₂. Таким образом, указанные перемещения плеч гимнаста в стороны, противоположные направлениям маха, являются механизмом управления динамическим равновесием.

Рис.179

Частным случаем проявления динамической устойчивости являются действия гимнаста в приземлениях после выполнения соскоков со снарядов, опорных и акробатических прыжков. Приземлению всегда предшествует полет, в котором можно выделить три основных варианта: полет без горизонтального перемещения, полет с перемещением вперед, полет с перемещением назад. В каждом из полетов могут выполняться элементы без вращений, с вращениями вперед и с вращениями назад. Для того, чтобы гимнаст устоял после контакта его ног с поверхностью приземления, необходимо остановить продвижение и вращение. Для этой цели гимнаст делает «упреждающую» постановку ног на опору, не дожидаясь пока ОЦМ тела окажется в зоне площади опоры ног.

10.3. Пространственно–временные характеристики движений в гимнастике

Движения тела гимнаста, выполняющего упражнение, в широком смысле слова протекают в пространстве и во времени. Эти движения безотносительно причин их вызывающих изучает кинематика – составная часть науки механики. Можно также сказать, что в процессе выполнения упражнения тело гимнаста перемещается по некоторому пути за определенное время, т.е. в кинематике в качестве основных параметров принимаются путь и время движения. Кроме основных, существуют производные параметры движения: скорость (первая производная) и ускорение (вторая производная). Путь движения также называется траекторией последнего и обозначается как ѕ или φ. Первый символ относится к прямолинейному движению и измеряется в линейных единицах: в метрах (м), сантиметрах (см), применительно к гимнастике. Для измерения угловых перемещений служат градусы (φ^°) и радианы (φ рад). Напомним, что угловой (круговой) путь в 360° соответствует пути в 2 П радиан, 180° – П радиан, 90°– 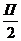радиан (П – отношение длины окружности к ее диаметру П ≈ 3,14).

Основные формы траектории движений, характерные для гимнастики, представляют собой или параболу, или замкнутую кривую, приближающуюся к окружности, или часть этой кривой. Параболическую кривую (рис.180) описывает тело гимнаста при соскоках с перекладины, в некоторых опорных и акробатических прыжках. Траекторию, близкую к окружности или ее части, описывает тело гимнаста при выполнении многих упражнений на снарядах (оборотов, махов и др.).

Рис. 180

Как видно из рис.180, высота и дальность полета гимнаста зависят от начальной скорости Vо и угла вылета. Время полета зависит только от его высоты и определяется формулой: t= 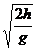, где h – максимальная высота полета, а g – ускорение свободного падения.

В кинематике гимнастических упражнений линейная скорость измеряется в м/с (метры в секунды), а угловая скорость – в рад/с (радианы в секунду). Заметим, что величина линейной скорости в гимнастических упражнениях может достигать 18–20 м/с (например, линейная скорость стоп гимнаста, выполняющего большой оборот на перекладине), а угловая скорость – 12–14 рад/с (например, при выполнении тройного сальто). Для сравнения: угловая скорость при выполнении обычного большого оборота на перекладине составляет около 3 рад/с.

Существует взаимосвязь между линейной скоростью и радиусом вращения. Так в упомянутом большом обороте звенья тела гимнаста имеют разные линейные скорости: чем дальше звено от оси вращения (грифа перекладины), тем больше его линейная скорость (рис.181). Вместе с этим в показанном примере угловая скорость всех звеньев тела одинакова (если пренебречь незначительным взаимным перемещением звеньев друг относительно друга). Искомая взаимосвязь линейной скорости и радиуса вращения видна из формулы: V = WR, т.е. V₁ = WR₁, V₂ = WR₂.

Рис. 181

Оси вращения тела гимнаста

В большинстве гимнастических движений имеется вращательная составляющая, поэтому весьма важно для анализа упражнений определить оси, вокруг которых происходит вращение.

Принято различать три взаимно перпендикулярные оси вращения, связанные с телом гимнаста: поперечную (фронтальную), переднезаднюю (сагиттальную), продольную. Большинство гимнастических упражнений выполняется с вращениями вокруг фронтальной оси (махи вперед и назад, обороты, сальто и т.д.). Вокруг сагиттальной оси происходит вращение при выполнении переворотов боком, махов на коне, боковых сальто и др. Вокруг продольной оси выполняются повороты («винты», пируэты). Оси вращения могут быть вещественными (материальными), т.е. принадлежать снаряду (например, грифу перекладины, жердям брусьев в продольном положении и др.) и мнимыми (воображаемыми) (например, параллельных брусьях или кольцах). Оси вращения могут быть также неподвижными (закрепленными) и подвижными (свободными), которые перемещаются вместе с гимнастом (например, в акробатических прыжках, в полете при соскоках со снарядов и т.д.). В гимнастике (особенно на снарядах) много упражнений, в которых вращение носит сложный характер (махи, обороты, сальто, перелеты и другие движения с поворотами). В этих случаях тело гимнаста вращается одновременно вокруг двух и даже трех осей (например, в соскоке сальто с поворотами на 720° с перекладины).

Каждой оси, вокруг которой происходит вращение тела гимнаста, соответствует плоскость, где протекают движения: для фронтальной оси – сагиттальная плоскость, для передне–задней оси – фронтальная или лицевая плоскость, для продольной оси – горизонтальная плоскость.

10.4. Действие сил, обеспечивающих движения

Динамика – часть науки механики, в которой изучаются движения тел с учетом причин, вызывающих движение, т.е. действующих сил.

В принципиальном плане понятие динамики раскрывается основным уравнением динамики: F = ma, где F – действующая сила, m – масса (мера инертности) тела, a – ускорение движения.

Силы, действующие на физические тела, в том числе и на тело гимнаста, имеют несколько разновидностей. По отношению к телу гимнаста силы могут быть внешними и внутренними, активными и пассивными, о чем подробно говорится в курсе биомеханики. Ниже будут рассмотрены некоторые вопросы динамики гимнастических упражнений с учетом основных сил, действующих на тело гимнаста.

Одна из основных сил, действующих при выполнении гимнастических упражнений – сила тяжести Р. Эта сила – внешняя и может проявляться как активная (например, в первой половине большого оборота) и как пассивная (во второй половине этого упражнения). Другими внешними силами являются: сила реакции опоры – F_оп , сила инерции – F_ин , сила трения ладоней о снаряд – F_mp, упругие силы деформации снарядов – F _уп. Внутренними силами являются силы тяги мышц (активные силы), сопротивления трению в суставах, фасциях (пассивные силы). За счет активных внутренних сил изменяется взаимное расположение звеньев тела гимнаста, выполняются бросковые, хлестообразные и другие маховые и силовые упражнения.

Рассмотрим более подробно силы инерции и их проявления в прямолинейном и криволинейном движениях. В любом из них при наборе скорости, силы инерции пассивны (отрицательны), они препятствуют движению, как бы тормозят движение. И наоборот: в конце движения, при уменьшении его скорости, силы инерции становятся активными (положительными), они способствуют движению. При выполнении оборотовых движений, кроме указанных сил инерции, возникают центростремительная F_цс и центробежная F_цб силы инерции. Первая приложена к телу гимнаста (условно к центру масс – ЦМ), а вторая – к связям, удерживающим гимнаста на снаряде (например, к точкам хвата за гриф перекладины). Обе силы равны по величине и противоположны по направлению действия: F_цс – от периферии к центру, а F _цб – от центра к периферии.

Рис. 182

Рассмотрим в общих чертах динамику большого оборота на перекладине. На рис. 182 изображена идеализированная траектория движения ОЦМ тела гимнаста, выполняющего большой оборот. На окружности (на самом деле траектория несколько отличается от окружности) обозначены наиболее характерные точки расположения ОЦМ, в которых показаны основные действующие силы. В точке 1 практически действует только сила тяжести Р, остальными можно пренебречь, т.к. скорость вращения гимнаста в этой точке очень мала. В точках 2, 4, 6, 8 сила тяжести раскладывается на нормальную Р_н и касательную Р_к составляющие. Первая из них направлена по радиусу, она изгибает гриф перекладины, а вторая направлена по касательной к траектории и вызывает вращение тела (в первой половине оборота) и наоборот препятствует вращению – во второй половине оборота. В точках 1 и 5 вся сила тяжести направлена на деформацию грифа, а также соответственно на сжатие и растягивание тела гимнаста. В точках 3 и 7 сила тяжести создает максимальные моменты вращения тела, причем в точке 3 момент вращения положительный, а в точке 7– отрицательный. Точки 2 и 8 называются точками относительной невесомости тела, т.к. в них все силы практически уравновешены, поэтому здесь возможны отпускания и одновременные перехваты рук. В точке 5 меняется свой знак вращательная сила инерции F_и , она из пассивной (отрицательной) становится активной (положительной). В этой точке достигает наибольшей величины сила, отрывающая гимнаста от перекладины, т.к. здесь происходит сложение силы тяжести и центробежной силы инерции F_цб, величина которой зависит от массы тела гимнаста и скорости его вращения: F _цб. = 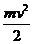= mw²R., т.к. v=wR

В качестве резюме к динамике гимнастических упражнений на примере большого оборота, еще раз обсудим действующие силы в одной из условных точек траектории движения ОЦМ гимнаста (по рис. 183). Например, в точке 4 действуют: сила тяжести Р, разложенная на нормальную Р_н и Р_к составляющие, F_и – вращательная сила инерции, направленная против движения, F _цс – центростремительная сила инерции, приложенная к ОЦМ. К этой точке также относится центробежная сила инерции F_цб, приложенная не к самому телу, а к связям, удерживающим тело (к грифу перекладины).

В приведенном примере подчеркивается сущность понятия динамики, в котором движение является следствием взаимодействия сил.

Работа и мощность при выполнении гимнастических упражнений

Механическая (физическая) работа гимнаста определяется по формуле А=FS, где А – работа, F – действующая сила, S– путь, пройденный телом под действием силы F. Работа измеряется в килограммометрах (кгм).

Величина работы, совершаемой гимнастом, зависит от ряда причин, главные из которых: структура упражнения, применяемая техника, физические данные гимнаста. Например, гимнаст, выполняющий подъем силой на кольцах, проделывает большую работу, чем при обычном подтягивании в висе, т.к. во втором случае больше путь, на котором преодолевается вес гимнаста.

Мощность определяется по формуле: N= 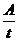, где N – мощность,

А – совершаемая работа, t – время, в течении которого выполняется работа. Выполнение многих гимнастических упражнений требует действий высокой мощности. К ним относятся современные опорные и акробатические прыжки, соскоки с многократными вращениями и др. Для выполнения таких упражнений гимнаст должен обладать высоким уровнем развития физических качеств, особенно силовых и скоростно–силовых.

Следует заметить, что несмотря на принципиальную возможность оценки двигательной деятельности гимнастов по показателям работы и мощности, в науке и практике по гимнастике используются другие критерии. В частности, скоростно–силовые качества гимнастов, где проявляется мощность, определяются показателями прыгучести, бегом на 20 м, быстротой лазания по канату и др. Физическую работу гимнастов принято оценивать опосредованно по количеству выполненных упражнений.

10.4.1. Некоторые законы механики и их проявление при

выполнении гимнастических упражнений

Закон сохранения и превращения механической энергии

Наиболее ярко этот закон проявляется при выполнении упражнений, в которых происходит чередование относительно высокого и низкого положений гимнаста, например, в прыжках на батуте, в больших оборотах на перекладине и кольцах и др.

Существуют два вида механической энергии: потенциальная и кинетическая, которые соответственно обозначаются: Е_п = mgh и Е_к = 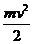, где m –

масса тела, g – ускорение свободного падения, h – высота подъема тела, v – линейная скорость движения тела.

В идеализированном упражнении (при отсутствии внешнего сопротивления) Е_п + Е_к = 0, т.е. потенциальная энергия полностью превращается в кинетическую и обратно. Поясним это на примере большого оборота на перекладине (рис. 183).

Рис. 183

В положении 1 тело гимнаста поднято на высшую точку траектории движения и поэтому обладает максимальным запасом потенциальной энергии. В то же время кинетическая энергия гимнаста в этом положении минимальна, т.к. скорость его очень мала. По мере продвижения гимнаста сверху вниз, его потенциальная энергия превращается в кинетическую и в нижней точке траектории становится минимальной, а кинетическая энергия достигает максимальной величины, т.к. здесь скорость движения максимальна. Во второй половине оборота, при движении гимнаста кверху, картина меняется на противоположную: кинетическая энергия превращается в потенциальную и тело возвращается в положение 1. Конечно, в действительности, без дополнительного притока энергии, тело гимнаста не сможет вернуться в исходное положение 1, т.к. часть энергии затрачивается на преодоление трения ладоней о гриф перекладины. Необходимая «подпитка» оборота осуществляется за счет активных бросковых, хлестовых движений гимнаста во второй половине упражнения.

Закон сохранения количества движения

Количеством движения тела называется произведение его массы на скорость движения, т.е. К=mv.

Существует закон механики, согласно которому сумма количеств движения частиц (частей), образующих замкнутую систему (т.е. систему, не взаимодействующую с другими телами), остается постоянной величиной

_n

K= Σ m_iv_i, где i – частица тела

^{I= 1}

Тело гимнаста можно считать замкнутой системой только тогда, когда оно находится в безопорном положении, в полете. В этом случае перемещение любого звена тела в каком–либо направлении вызовет соответствующее перемещение смежного звена в противоположном направлении, т.к. согласно рассматриваемому закону сумма количеств движения системы остается постоянной величиной.

Однако, когда тело гимнаста связано с опорой, указанный закон механики будет проявляться с некоторыми особенностями, суть которых состоит в перераспределении количества движения в системе и передаче последнего на звено, связанное с опорой. Поясним сказанное на примере подъема разгибом из упора на руках на брусьях (рис. 184).

Рис. 184

Из положения 1 гимнаст резким движением направляет ноги вверх – вперед и почти одновременно отталкивается плечами от жердей. Благодаря тому, что определенное количество движения от «приторможенных» ног (положение 2) передается туловищу, существенно облегчается подъем в упор (положение 3). Другим примером проявления данного закона может служить прыжок вверх со взмахом руками. В этом случае ускоренное движение рук вверх с последующей их остановкой неизбежно приведет к некоторому увеличению количества движения всего тела и в конечном итоге – высоты прыжка.

Закон сохранения момента количества движения

При вращения тела его количество движения измеряется моментом относительно оси вращения: М_кg = mvr.

Так как Ư = WR, то М_кg = mvr², но mr² = J (момент инерции тела), поэтому М_кg = JW = const. Для изолированной системы момент количества движения определяется произведением момента инерции на угловую скорость, причем с течением времени он остается постоянной величиной (const). Из приведенной формулы следует, что при неизменном М_кg величины и JW связаны обратной зависимостью: изменение момента инерции тела гимнаста обратно пропорционально изменению угловой скорости тела. Проявление этого закона можно видеть, например, в соскоках сальто с перекладины. При обычном сальто прогнувшись гимнаст описывает в воздухе относительно медленное вращение. При двойном сальто гимнаст выполняет группировку и тем самым уменьшает момента инерции, вследствие чего автоматически возрастает его угловая скорость. Перед приземлением гимнаст разгруппировывается, за счет чего уменьшается его «крутка», т.к. возрастает момент инерции. Таким образом, изменяя в полете позу, а следовательно и момент инерции тела, гимнаст имеет возможность управлять скоростью безопорного вращения.

Следует заметить, что действие закона сохранения момента количества движения распространяется также на многие случаи выполнения движений на опоре (обороты, подъемы, прыжки). Здесь, благодаря перераспределению моментов количества движения звеньев тела, гимнаст имеет возможность, например, ускорить или замедлить движение одного звена за счет другого, смежного.

10.5. О структуре динамических (маховых) упражнений

Под структурой в широком смысле слова следует понимать состав, строение.

Гимнаст, выполняющий упражнение, производит определенные двигательные действия, в которых можно выделить стадии, фазы: подготовительную, основную и завершающую, названия которых в целом отражают их назначение и содержание.

Подготовительные действия создают оптимальные условия для выполнения последующей более важной части упражнения. Состав подготовительных действий зависит от того, какое упражнение выполняется, к какой двигательной структуре оно относится. Так для движений, выполняемых большим махом, подготовительные действия включают максимальное удаление, «оттягивание» гимнаста от оси вращения и набор достаточно большой скорости движения в висе или в упоре. Для движений разгибом гимнасту целесообразно сперва согнуться в тазобедренных суставах, а затем разогнуться в стадии основных действий.

Основные действия могут быть различной сложности. Проще те, в которых тело гимнаста все время вращается в одном направлении, например, в переворотах, оборотах, многих подъемах. В таких упражнениях активные двигательные действия гимнаста совпадают с направлением движения тела и называются моноциклом. Различают также другие типы основных действий: дубльцикл и контрцикл. В дубльцикле гимнаст дважды делает «подпитку» движения по его ходу за счет собственных двигательных действий, например, при выполнении высокого соскока переворотом ноги врозь на кольцах или соскока «хлестом» с перелетом через перекладину. В контрцикле основных действий происходит изменение направления вращения тела гимнаста. Простейшие примеры: соскоки махом вперед или дугой с перекладины, подъемы махом вперед на брусьях или кольцах. Более сложные упражнения: подъем дугой на брусьях, соскок дугой с последующим сальто вперед с перекладины, перелет Ткачева на перекладине. В этих и других упражнениях подобного типа тело гимнаста в начале упражнения вращается назад, а затем, благодаря активным действиям гимнаста, меняет направление движения на противоположное. Происходит как бы противопоставление двух моноциклов.

Завершающие действия – последняя стадия двигательных действий гимнаста, которые придают всему упражнению законченный вид – гимнаст приходит в конечное положение. Предложенное Н.А. Курьеровым и рассмотренное выше деление движения на части (стадии, фазы) носит условный характер. А действительности, выполняемое упражнение – непрерывное движение, а выделение в нем отдельных стадий полезно для анализа и в конечном итоге – для обучения упражнению.

Date: 2015-07-23; view: 374; Нарушение авторских прав