Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Сопряжение прямой линии с окружностью
|
|
Если радиус сопряжения Rс прямой линии и окружности радиусом R задан, то при определении параметров сопряжений следует исходить из следующих положений:
а) множество точек, удаленных от прямой на расстояние Rс, есть две параллельные прямые, отстоящие от заданной на расстоянии Rс;
б) множество точек, удаленных от окружности на расстояние Rс, есть две концентрические окружности, радиусы которых равны сумме или разности R и Rс;
в) точки пересечения множеств, указанных в пунктах «а» и «б», являются центрами сопряжений;
г) точка сопряжения заданной прямой есть основание перпендикуляра, опущенного из центра сопряжения на эту прямую;
д) точка сопряжения заданной окружности лежит на прямой, соединяющей центр этой окружности с центром сопряжения.
По положению центра заданной окружности и центра сопрягающей дуги относительно общей касательной различают внешнее и внутреннее сопряжения. Если центр окружности и центр сопряжения лежат по разные стороны от касательной, то такое сопряжение считают внешним, а если эти центры располагаются по одну сторону от касательной, — внутренним.
Рассмотрим несколько примеров.
Пусть заданы окружность с радиусом R1 (рис. 1.23) и центром в точке О и прямая АВ. Требуется выполнить внешнее сопряжение радиусом Rс.
Выбрав на прямой АВ произвольную точку M, восставим из нее перпендикуляр к АВ и отложим на нем отрезок МN, равный Rс.
| Рис. 1.24 |
| Рис. 1.23 |
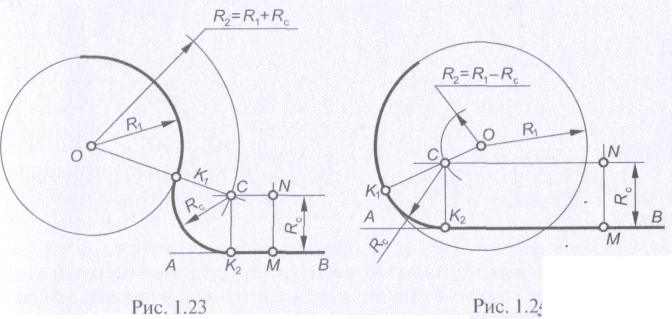Через точку N проведем прямую, параллельную АВ (см. п. «а»). Из точки О, как из центра, радиусом R2, равным сумме радиусов R1 и Rс, проведем дугу окружности (см. п. «б»). Точка С пересечения прямой, проходящей через точку N, с дугой радиусом R2 является центром сопряжения (см. п. «в»). Из точки С опустим перпендикуляр на АВ. Основание K2 перпендикуляра и будет точкой сопряжения окружности с прямой (см. п. «г»). Соединим точки О и С прямой линией, пересечение которой с заданной окружностью определяет точку их сопряжения К1 (см. п. «д»).
Завершая построение, следует из центра С радиусом Rс провести дугу окружности от точки К1 до точки К2.
Пусть заданы окружность с радиусом R1 (рис. 1.24) и центром в точке О и прямая АВ. Требуется выполнить внутреннее сопряжение радиусом Rс.
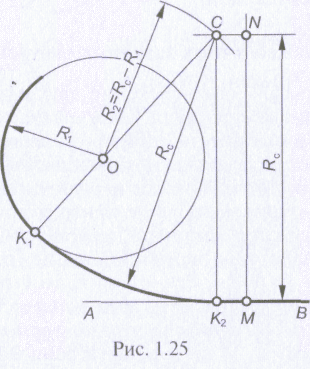Требуемые построения не отличаются существенно от рассмотренных в предыдущем примере и имеют лишь две особенности. Множество точек плоскости, удаленных от заданной окружности на расстояние Rс, представляет собой концентрическую окружность, радиус которой К2 равен разности радиусов R1 и Rс. Точка K1 сопряжения располагается на продолжении прямой, соединяющей центры заданной и сопрягающей окружностей.
Пусть заданы окружность с радиусом R1 (рис. 1.25) и центром в точке О и прямая АВ. Требуется выполнить внутреннее сопряжение радиусом Rс.
Отличие данной задачи от предыдущей состоит в том, что радиус сопряжения Rс больше радиуса R1 заданной окружности. В этом случае радиус R2 также определяется как разность радиуса сопряжения и радиуса заданной окружности, однако уменьшаемое и вычитаемое должны быть выбраны так, чтобы эта разность получилась положительной.
Date: 2015-07-23; view: 1184; Нарушение авторских прав