
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Взаимное расположение двух плоскостей
|
|
Плоскости могут совпадать, быть параллельными или пересекаться по прямой.
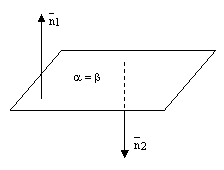
рис.3.
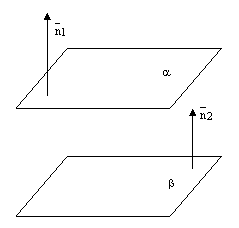
рис.4.

рис.5.
Теорема. Пусть
 и
и 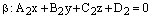
– общие уравнения двух плоскостей. Тогда:
1) если 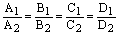 , то плоскости совпадают;
, то плоскости совпадают;
2) если 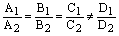 , то плоскости параллельны;
, то плоскости параллельны;
3) если  или
или 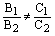 , то плоскости пересекаются и системауравнений
, то плоскости пересекаются и системауравнений
 (6)
(6)
является уравнениями прямой пересечения данных плоскостей.
Доказательство. Первое и второе условия теоремы равносильны коллинеарности нормальных векторов данных плоскостей:
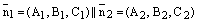 .
.
Если 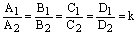 , то
, то 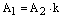 ,
, 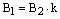 ,
, 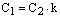 ,
, 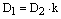 и уравнение плоскости
и уравнение плоскости 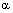 принимает вид:
принимает вид:
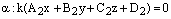
Коэффициент пропорциональности k не может быть равен нулю, т.к. 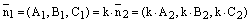 и при
и при 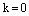 получаем, что
получаем, что 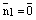 , что противоречит определению нормального вектора. Следовательно,уравнение плоскости
, что противоречит определению нормального вектора. Следовательно,уравнение плоскости 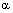
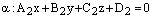
совпадает с уравнением плоскости 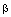 , а это означает, что плоскости совпадают.
, а это означает, что плоскости совпадают.
Если 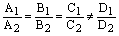 , то это означает коллинеарностьнормальныхвекторов обеих плоскостей, а значит плоскости либо параллельны, либо совпадают. Но в этом случае плоскости не могут совпадать и остается единственная возможность их параллельности.
, то это означает коллинеарностьнормальныхвекторов обеих плоскостей, а значит плоскости либо параллельны, либо совпадают. Но в этом случае плоскости не могут совпадать и остается единственная возможность их параллельности.
Третье условие теоремы равносильно тому, что нормальные векторыплоскостей не коллинеарные, а потому они не совпадают и не параллельны, а следовательно, они пересекаются. Из геометрии известно, что линия пересечения двух плоскостей является прямой.
Точка М лежит на прямой пересечения двух плоскостей 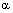 и
и 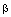 тогда и только тогда, когда она лежит одновременно на обеих плоскостях и еекоординаты удовлетворяют обоим уравнениям системы (6), т.е. являются решением этой системы. А это означает, что система (6) является уравнениями прямой пересечения плоскостей, ч.т.д.
тогда и только тогда, когда она лежит одновременно на обеих плоскостях и еекоординаты удовлетворяют обоим уравнениям системы (6), т.е. являются решением этой системы. А это означает, что система (6) является уравнениями прямой пересечения плоскостей, ч.т.д.
Теорема доказана.
16.Олределения функции.Способы задания функции:
В тетрадке
17.Элементарные функции:
Основными элементарными функциями являются: постоянная функция (константа), корень n -ой степени, степенная функция, показательная, логарифмическая функция, тригонометрические и обратные тригонометрические функции.
- Постоянная функция (константа), ее график и свойства.
- Корень n -ой степени, свойства и график.

- Степенная функция, ее график и свойства.
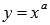
- Показательная функция, свойства, график.
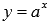
- Логарифмическая функция, ее свойства, графическая иллюстрация.
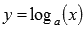
- Свойства и графики тригонометрических функций.
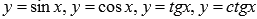
- Обратные тригонометрические функции (аркфункции), их свойства и графики.
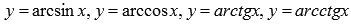
18.Свойства функции:
1) Область определения функции и область значений функции.
Область определения функции - это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена.
Область значений функции - это множество всех действительных значений y, которые принимает функция.
В элементарной математике изучаются функции только на множестве действительных чисел.
2) Нули функции.
Нуль функции – такое значение аргумента, при котором значение функции равно нулю.
3) Промежутки знакопостоянства функции.
Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.
4) Монотонность функции.
Возрастающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Убывающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
5) Четность (нечетность) функции.
Четная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат.
Нечетная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = - f(x). График нечетной функции симметричен относительно начала координат.
6) Ограниченная и неограниченная функции.
Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x. Если такого числа не существует, то функция - неограниченная.
7) Периодическость функции.
Функция f(x) - периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. (Тригонометрические формулы).
Изучив данные свойства функции Вы без проблем сможете исследовать функцию и по свойствам функции сможете построить график функции. Также посмотрите материал про таблицу истинности, таблицу умножения, таблицу Менделеева, таблицу производных и таблицу интегралов.
19.Техника вычисления приделов:
В тетрадке
20Понятие производной
Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).
Процесс вычисления производной называется дифференци́рованием. Обратный процесс — нахождение первообразной —интегрирование.
21.Геометрический смысл производной:
Геометрический смысл производной
Построим произвольный график некой функции y = f (x) на координатной плоскости, построим касательную в точке xо, обозначим угол между прямой о осью ox как α (альфа)
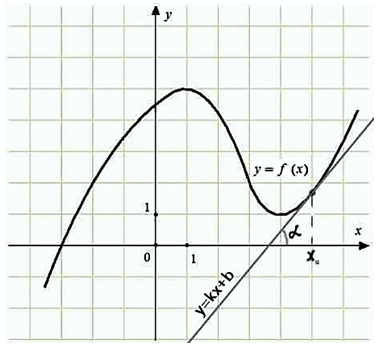
Из курса алгебры известно, что уравнение прямой имеет вид:


То есть производная функции y = f(x) в точке x0 равна угловому коэффициенту касательной:
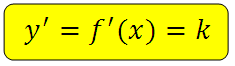
А угловой коэффициент в свою очередь равен тангенсу угла α (альфа), то есть:
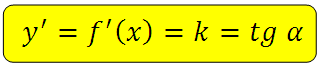
Угол α (альфа) может быть меньше, больше 90 градусов или равен нулю.
Проиллюстрируем, два случая:
1. Угол наклона касательной больше 90 градусов (тупой угол).
2. Угол наклона касательной равен нулю градусов (касательная параллельна оси ох).
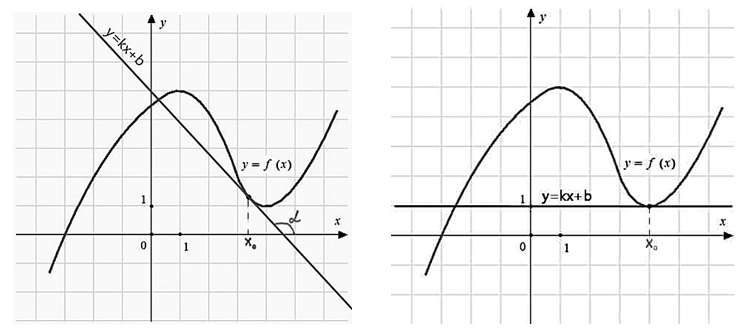
То есть задачи, в которых дан график функции, касательная к этому графику в определённой точке, и требуется найти производную в точке касания, сводятся к нахождению углового коэффициента касательной (либо тангенса угла наклона касательной, что одно и тоже).
Ниже рассмотрим решение таких задач через нахождение тангенса угла между касательной и осью абсцисс (осью ох), ещё один способ решения (нахождение производной через угловой коэффициент) рассмотрим в недалёком будущем. Также будем рассматривать задачи, где требуется знание свойств производной для чтения графика функции. Не пропустите, подпишитесь на обновлениеблога.
Обратите внимание, что на координатной плоскости обозначены две точки через которые проходит касательная – это очень важный момент (можно сказать ключевой в этих задачах).
Что ещё потребуется — это знание формулы приведения для тангенса тупого угла.
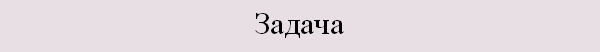
На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции y = f(x) в точке x0.
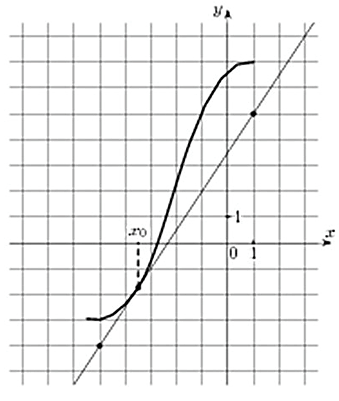
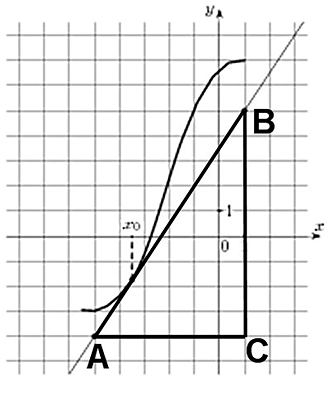
Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Для того, чтобы найти тангенс этого угла, построим прямоугольный треугольник, где отрезок ограниченный двумя точками на графике, будет являться гипотенузой, а катеты параллельны осям. В данной задаче это точки (–5; –4), (1; 5).
Напомню: тангенсом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему.
Катеты определяем по числу клеток.
Угол наклона касательной к оси абсцисс равен углу BAC, так как катет АС параллелен оси ох. Значит
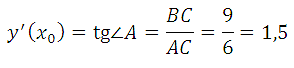
Ответ: 1,5
22.Связь между непрерывной и дифференцируемой функцией:
Имеет место следующая теорема. Если функция 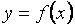 дифференцируема в точке
дифференцируема в точке 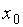 , то она непрерывна в этой точке.
, то она непрерывна в этой точке.
Доказательство. Так как функция 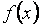 дифференцируема в точке
дифференцируема в точке 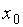 , то существует конечный предел
, то существует конечный предел 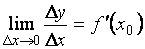 . Тогда по теореме о связибесконечно малой с функцией, имеющей конечный предел, будем иметь
. Тогда по теореме о связибесконечно малой с функцией, имеющей конечный предел, будем иметь
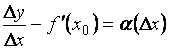 ,
,
где 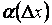 - бесконечно малая величина при
- бесконечно малая величина при 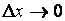 .
.
Откуда
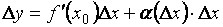 .
.
Переходя в этой формуле к пределу при 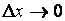 , получим по свойствам бесконечно малых, что
, получим по свойствам бесконечно малых, что 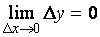 .
.
Следовательно, по одному из определений непрерывности функция 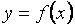 в точке
в точке 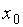 является непрерывной.
является непрерывной.
Обратная теорема, вообще говоря, неверна, т.е. функция может быть непрерывной в данной точке, но не быть дифференцируемой в этой точке.
В качестве примера исследуем функцию  в точке
в точке 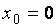 , которая непрерывна в точке
, которая непрерывна в точке 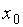 (впрочем, как и во всех других точках числовой прямой). В этой точке ее левосторонний и правосторонний пределы равны нулю, что совпадает со значением самой функции в точке
(впрочем, как и во всех других точках числовой прямой). В этой точке ее левосторонний и правосторонний пределы равны нулю, что совпадает со значением самой функции в точке 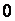 .
.
По определению
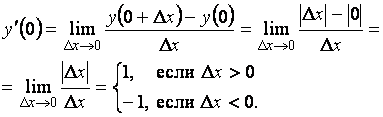
Таким образом, функция  в точке
в точке 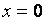 имеет конечные, но не равные друг другу односторонние производные (левая равна
имеет конечные, но не равные друг другу односторонние производные (левая равна 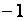 , а правая равна
, а правая равна 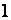 ). Поэтому она не имеет производной в этой точке и не является в ней дифференцируемой.
). Поэтому она не имеет производной в этой точке и не является в ней дифференцируемой.
23.таблица производных
Если x - независимая переменная, то:
| Таблица производных. Табличные производные. | |
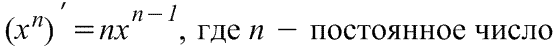 Производная степенной функции Производная степенной функции
| 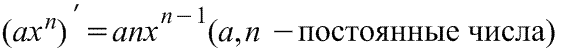 Производная степенной функции Производная степенной функции
|
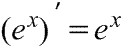 Производная экспоненциальной функции Производная экспоненциальной функции
| 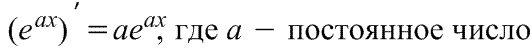 Производная экспоненты Производная экспоненты
|
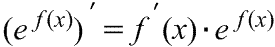 Производная сложной экспоненциальной функции Производная сложной экспоненциальной функции
| 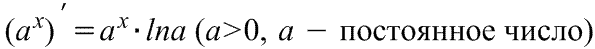 Производная экспоненциальной функции Производная экспоненциальной функции
|
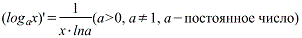 Производная логарифмической функции Производная логарифмической функции
| 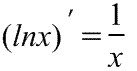 Производная натурального логарифма Производная натурального логарифма
|
 Производная натурального логарифма функции
Производная натурального логарифма функции
| |
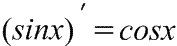 Производная синуса Производная синуса
| 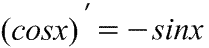 Производная косинуса Производная косинуса
|
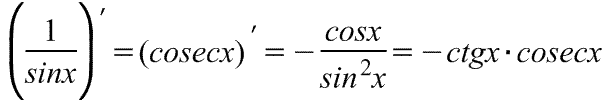 Производная косеканса Производная косеканса
|  Производная секанса Производная секанса
|
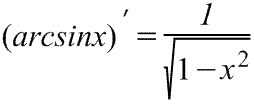 Производная арксинуса Производная арксинуса
| 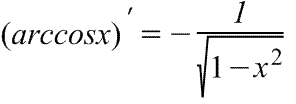 Производная арккосинуса Производная арккосинуса
|
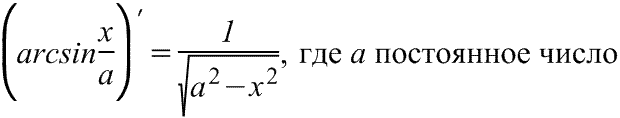 Производная арксинуса Производная арксинуса
|
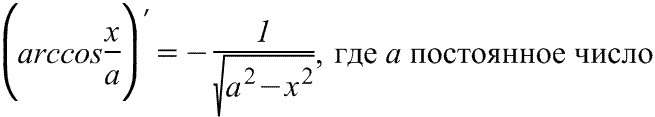 Производная арккосинуса Производная арккосинуса
|
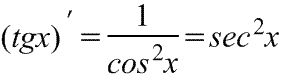 Производная тангенса Производная тангенса
| 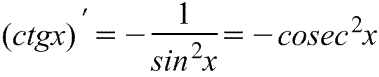 Производная котангенса Производная котангенса
|
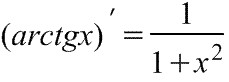 Производная арктангенса Производная арктангенса
| 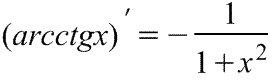 Производная арккотангенса Производная арккотангенса
|
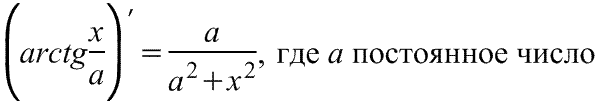 Производная арктангенса Производная арктангенса
| 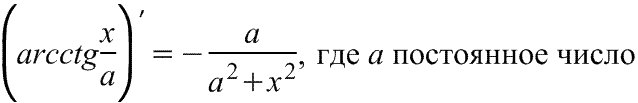 Производная арккотангенса Производная арккотангенса
|
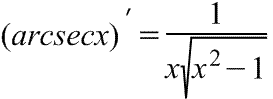 Производная арксеканса Производная арксеканса
| 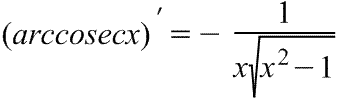 Производная арккосеканса Производная арккосеканса
|
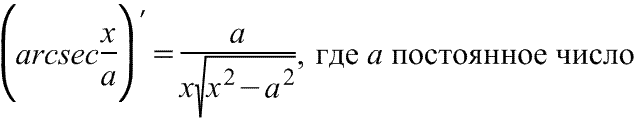 Производная арксеканса Производная арксеканса
| 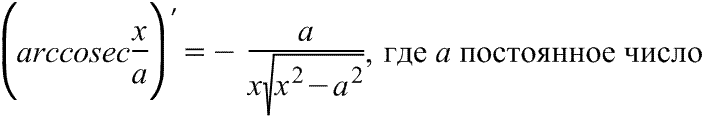 Производная арккосеканса Производная арккосеканса
|
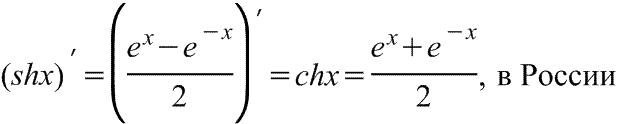 Производная гиперболического синуса Производная гиперболического синуса
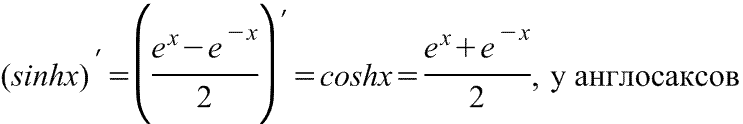 Производная гиперболического синуса в английской версии Производная гиперболического синуса в английской версии
| 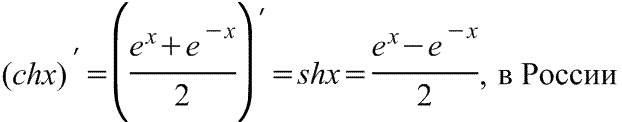 Производная гиперболического косинуса Производная гиперболического косинуса
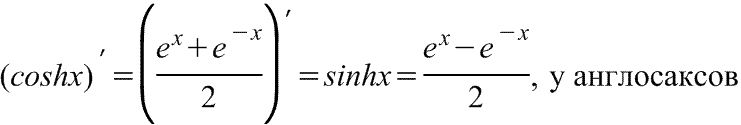 Производная гиперболического косинуса в английской версии Производная гиперболического косинуса в английской версии
|
 Производная гиперболического тангенса Производная гиперболического тангенса
| 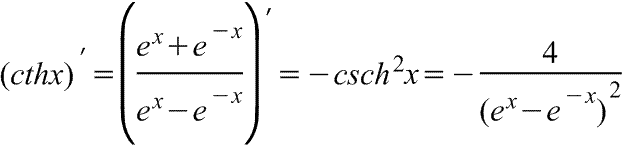 Производная гиперболического котангенса Производная гиперболического котангенса
|
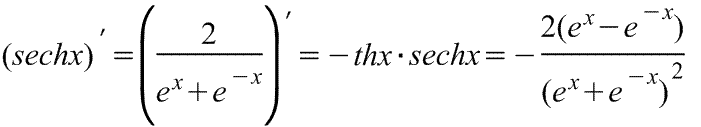 Производная гиперболического секанса Производная гиперболического секанса
| 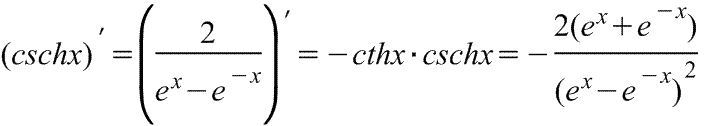 Производная гиперболического косеканса Производная гиперболического косеканса
|
24.Дифференциал функции
Дифференциал функции
Пусть функция 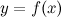 дифференцируема в точке
дифференцируема в точке  , то есть приращение этой функции можно представить в виде суммы двух слагаемых: линейного относительно
, то есть приращение этой функции можно представить в виде суммы двух слагаемых: линейного относительно 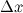 и нелинейного членов:
и нелинейного членов:
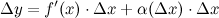
где 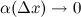 при
при 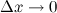 .
.
Date: 2015-07-23; view: 879; Нарушение авторских прав