Основные сведения. Общая схема анализа ЭМВ в реальных средах

Общая схема анализа ЭМВ в реальных средах. ЭМП в виде плоских ЭМВ в заданной среде удобно анализировать по следующей схеме.

1. Находим tg d по формуле (2.15).

Классифицируем среду (диэлектрик, проводник, полупроводник) в зависимости от значения tg d по формулам (2.16).

2. Находим a и b по формулам для соответствующего вида среды:

общий случай и полупроводник – (5.13) и (5.14);

диэлектрик – (6.1) и (6.2);

проводник – (7.1).

3. Находим характеристики ЭМВ (групповая и фазовая скорость, длина волны, затухание, волновое сопротивление и т. п.) и записываем формулу плоской ЭМВ (5.11) или (5.12) для соответствующей среды:

полупроводник – тема 5, формулы (5.15)–(5.20), (5.22)–(5.24);

диэлектрик – тема 6, формулы (6.3)–(6.5);

проводник – тема 7, формулы (7.2)–(7.4).

Поляризацию ЭМВ определяют по ориентации вектора .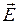

Плоскостью поляризации называют плоскость, проходящую через направление распространения и вектор 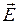. Считаем, что ось x ориентирована горизонтально, а ось y – вертикально. Достаточно рассмотреть поведение 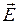, так как связь с 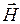известна: .

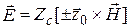Запишем мгновенное значение 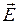в ДСК:

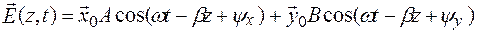. (8.1)

Линейно поляризованной называют волну, у которой направление вектора 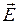(а значит, и 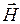) не изменяется с течением времени. Если в формуле (8.1) B = 0, то 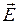имеет только горизонтальную составляющую, в этом случае ЭМВ имеет горизонтальную поляризацию. Если в формуле (8.1) A = 0, то 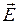имеет только верти­каль­ную составляющую, в этом случае ЭМВ поляризована вертикально.

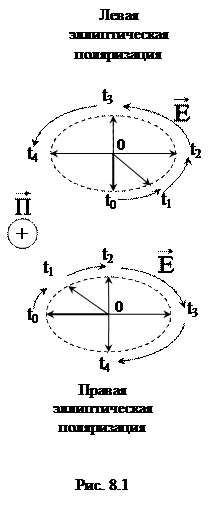
Поляризация называется эллиптической, если проекция вектора 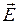на плоскость, перпендикулярную направлению распространения, пред­­ставляет собой эллипс (рис. 8.1).

Если фазовый сдвиг между компонентами составляет Dy = p/2+pn, то конец вектора 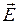с течением времени опишет эллипс.

Пусть y_x = 0, тогда E_x ~ 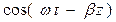, а E_y ~ 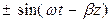. В этом случае

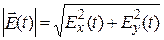
представляет собой эллипс с полуосями A и B.

Эллиптическую поляризацию можно получить сложением двух ЭМВ ортогональных линейных поляризаций.

Круговая поляризация (проекция 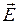на плоскость, перпендикулярную направлению распространения, есть круг) – частный случай эллиптической, когда полуоси эллипса равны между собой. При этом амплитуда ЭМВ остается постоянной (). Угол J между мгновенным значением и осью x определяется соотношением [1, 11]

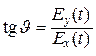Þ 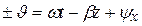. (8.2)

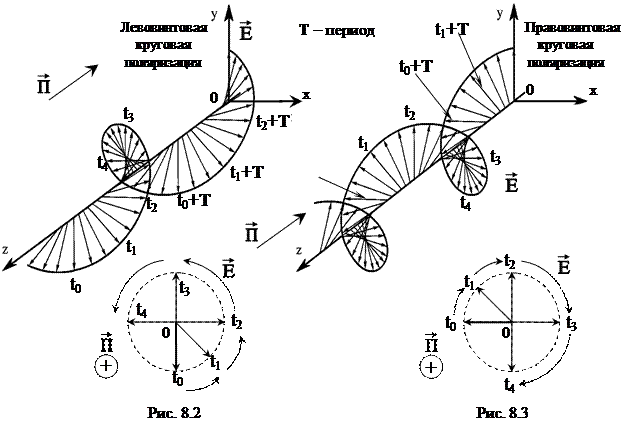
Из соотношения (8.2) следует, что в каждой фиксированной точке наблюдения в плоскости z = const угол J линейно возрастает со скоростью w с течением времени, изменяясь на 2p за время одного периода T (wT = 2p).

Направление вращения 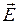определяется поведением проекции данного вектора на плоскость x0y (z = const). Если смотреть в направлении распространения ЭМВ, и вектор 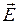вращается по часовой стрелке (рис. 8.1, 8.3), то такая поляризация называется правовинтовой. Если вращение происходит против часовой стрелки (рис. 8.1, 8.2), то эта поляризация – левовинтовая [1, 2].

Разделение ЭМВ по поляризации позволяет выполнять поляризационную селекцию сигналов. В каждом конкретном случае выбирается основная поляризация. В этом случае поляризация, ортогональная основной, будет паразитной. В идеале ЭМВ паразитная поляризация не должна приниматься антенной, настроенной на основной вид поляризации. Однако реально полностью подавить паразитную поляризацию не удается. На неоднородностях на трассе распространения ЭМВ и линии передачи может происходить изменение характеристик поляризации, что приводит к кросс-поляризации.

Например, в радиолокации для уменьшения мешающих отражений от водяных паров в атмосфере (гидрометеоров) используют разделение по поляризации. Если правовинтовая поляризация выбрана как основная, то в конструкцию антенны включают поляризационную систему, которая с минимальным ослаблением пропускает ЭМВ основной поляризации, но существенно ослабляет паразитную (левовинтовую) поляризацию.

Список рекомендуемой литературы: [ 1, гл. 10, с. 52–55; 2, с. 60–62; 3, гл. 10, с. 48–51; 4, с. 44–47; 5, с. 30–32; 6, с. 146–153; 7, с. 86–90; 9, с. 134–137; 10, с. 134–138; 11, с. 139–143; 12, с. 155–162; 13, с. 76–180].

Контрольные вопросы и задания

1. Укажите последовательность анализа ЭМП, распространяющегося в среде с заданными параметрами.

2. Что дает классификация ЭМ свойств сред в зависимости от tg d?

3. Дайте характеристику поведения коэффициента затухания ЭМВ для проводника и диэлектрика с ростом частоты.

4. Какова частотная характеристика коэффициента фазы для проводников и диэлектриков?

5. Дайте определение поляризации ЭМВ и укажите основные разновидности поляризации.

6. Можно ли из двух ЭМВ линейной поляризации получить ЭМВ круговой поляризации?

7. Можно ли из двух ЭМВ круговой поляризации получить ЭМВ линейной поляризации?

8. Что такое плоскость поляризации? Чем различаются правая и левая поляризации?

9. Что такое «кросс-поляризация»?

10. Антенна настроена на прием ЭМВ определенной поляризации. Будет ли она принимать ЭМВ с поляризацией, ортогональной основной?

Date: 2015-06-11; view: 445; Нарушение авторских прав