Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Основные сведения. После преобразования уравнений (2.5)–(2.8) [1–6] получаем дифференциальнуюформу теоремы Умова – Пойнтинга
|
|
После преобразования уравнений (2.5)–(2.8) [1–6] получаем дифференциальнуюформу теоремы Умова – Пойнтинга
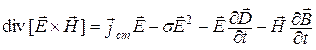. (4.1)
После интегрирования по объему (4.1) и преобразований получаем
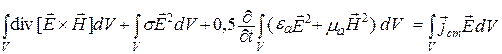. (4.2)
Каждое слагаемое в выражении (4.2) имеет размерность мощности
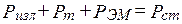. (4.3)
Уравнения (4.2)–(4.3) позволяют сформулировать теорему Умова –Пойнтинга: «Мощность стороннего источника в данном объеме расходуется на излучение, тепловые потери и изменение запаса энергии ЭМП» [1–3].
Мощность тепловых потерь (потерь проводимости) подчиняется закону Дж. Джоуля – Э. Ленца. Изменение запаса энергии имеет размерность мощности:
, (4.4)
где WЭМ – энергия ЭМП.
Вектор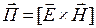 
называется вектором Пойнтинга. По теореме Остроградского – Гаусса [1–3] 
.
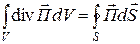Вектор Пойнтинга указывает направление распространения излучения, а его модуль представляет собой плотность потока мощностиизлучения.
В комплексной форме уравнения (4.2) и (4.3) имеют вид [1]
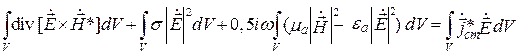; (4.5)
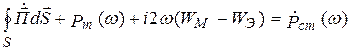, (4.6)
где 
; 
; 
,
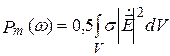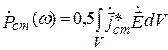а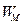 
и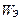 
– энергия магнитного и электрического полей соответственно.
Выражение (4.6) – баланс комплексных мощностей в объеме V.
Рассмотрим баланс ЭМ энергии (4.3) в контуре, представляющем замкнутую электрическую цепь из элементов с сосредоточенными параметрами (рис. 4.1).
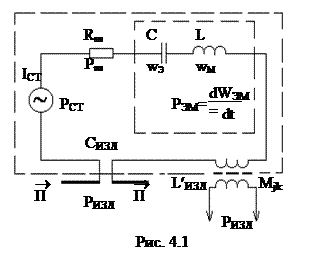Энергия стороннего источника расходуется на тепловые потери, которые сосредоточены в активном сопротивлении Rт, на изменение запаса ЭМ энергии в контуре (электрическая энергия накапливается в емкости C, а магнитная – в индуктивности L), на излучение из контура (элемент взаимной индуктивности Мik с другим контуром и «излучающий конденсатор» – электрический вибратор.
Выделим действительную и мнимую части уравнения (4.6)
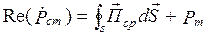; (4.7)
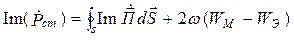. (4.8)
Действительная часть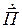 
характеризует перенос энергии через граничную поверхность области V в окрестности точки наблюдения, а мнимая часть 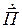– колебание энергии через ту же поверхность [1, 12].
Из выражения (4.7) следует, что средняя мощность стороннего источника тратится на тепловые потери в объеме V и на создание ЭМП за пределами V.
Из выражения (4.8) следует, что реактивная мощность стороннего источника расходуется на создание потока реактивной мощности через границу V и на создание запаса реактивной энергии в объеме V. Реактивная мощность характеризует процесс обмена энергией между источником и цепью. При Pр > 0 энергия запасается в магнитном поле, а при Pр < 0 – в электрическом.
Даже при отсутствии стороннего источника в V возможны колебания энергии при переходе электрической энергии в магнитную, и наоборот, подобно тому, как это происходит в колебательном LC -контуре без потерь [12].
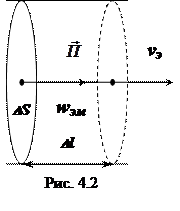
Скорость движения энергии (vЭ) определяется отношением вектора Пойнтинга к объемной плотности энергии ЭМВ. Из рис. 4.2 следует, что с одной стороны за время Dt энергия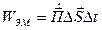 
заполняет объем DV=DSDl=DS vэ Dt, а, с другой стороны, 
.
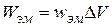После преобразований получим
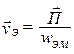. (4.9)
В случае изотропного источника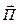 
будет направлен радиально от центра. Волновой фронт источника представляет собой сферу, которая будет увеличиваться с увеличением расстояния r от источника. При отсутствии потерь в пространстве на больших расстояниях от изотропного источника мощностью Pист его 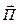можно оценить формулой
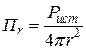. (4.10)
Список рекомендуемой литературы: [ 1, гл. 5, с. 24–26; 2, с. 64–74; 3, с. 25–27; 4, гл. 5, с. 24–26; 5, с. 15–17; 6, с. 49–58, 123–127; 7, с. 55–62; 8, с. 9–18; 9, с. 39–51, 57–59; 10, с. 43–50, 57–59; 11, с. 53–60; 12, с. 43–46, 55–60; 13, с. 40–51, 128–134; 15, с. 308–310].
Контрольные вопросы и задания
1. Сформулируйте закон баланса энергии для ЭМП.
2. Укажите физический смысл, правила ориентации, единицу измерения вектора Пойнтинга.
3. Назовите основные разновидности мощностей.
4. Проанализируйте баланс энергии ЭМП в замкнутом последовательном контуре с потерями и без потерь.
5. Определите среднее значение вектора Пойнтинга через комплексные амплитуды векторов ЭМП.
6. Какие величины характеризуют изменение запаса энергии в системе?
7. Объясните энергетический смысл комплексных проницаемостей сред.
8. Как можно определить скорость движения энергии ЭМВ?
9. Каков смысл мнимой части вектора Пойнтинга и мощности излучения?
10. Как определяется 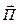изотропного источника?
Date: 2015-06-11; view: 462; Нарушение авторских прав