Основные сведения. Для анализа распространяющихся ЭМВ из системы уравнений Максвелла в дифференциальной форме целесообразно вывести уравнения

Для анализа распространяющихся ЭМВ из системы уравнений Максвелла в дифференциальной форме целесообразно вывести уравнения, которые зависят либо только от 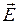, либо только от 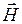. Если параметры среды (s, e, m) не зависят от координат и времени, то после преобразований получим [1–6]

; (5.1)

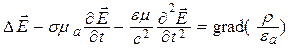. (5.2)

Как показали расчеты и эксперименты, константа с (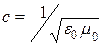) для ЭМП удивительным образом совпадает со значением скорости света в вакууме. Из этого был сделан вывод о том, что ЭМВ и свет имеют одну и ту же природу. В пространстве без потерь ЭМВ распространяются со скоростью света.

Уравнения (5.1) и (5.2) называют волновыми уравнениями Ж. Д’Аламбера [5, 12]. Если правая часть равна нулю, то уравнение называют однородным, а если нет – неоднородным. При отсутствии электрических зарядов (r = 0) уравнения (5.1) и (5.2) практически совпадают, что подтверждает равноправие векторов 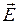и 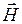у распространяющегося в пространстве ЭМП.

Несмотря на кажущуюся независимость уравнений (5.1) и (5.2), следует помнить о том, что у переменного ЭМП векторы 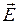и 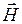связаны уравнениями Максвелла и не могут существовать друг без друга.

Волновые уравнения в комплексной форме имеют вид

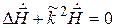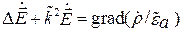; , (5.3)

где 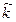– волновое число:

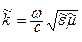. (5.4)

Уравнения (5.3) называют волновыми уравнениями Г. Гельмгольца. При отсутствии потерь проводимости (s = 0) исчезают вторые слагаемые в уравнениях (5.1) и (5.2), а также в (5.3)–(5.4) возможно упрощение:

.

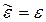Рассмотренные уравнения называются волновыми потому, что их решениями являются волны и, в частности, ЭМВ.

Фазовым фронтом волны называют поверхность, проходящую через точки с одинаковыми фазами, по форме этой поверхности определяется название волны (сфера – сферическая ЭМВ, плоскость – плоская и т. д.) [1–3].

Решение однородного волнового уравнения для плоских волн

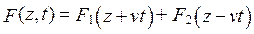. (5.5)

Каждое из слагаемых выражения (5.5) описывает возмущения F₁ и F₂, исходящие из точки z₀ в момент t = 0 и к моменту времени t приходящие в точку z = z₀ – vt для F₁ и в точку z = z₀ + vt для F₂ со скоростью v [1].

Для сферических волн решение волнового уравнения имеет вид:

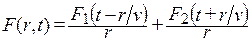. (5.6)

Первое слагаемое выражения (5.6) представляет собой сферическую волну, расходящуюся от источника. Второе слагаемое часто отбрасывают, поскольку волна, движущаяся внутрь источника, обычно не рассматривается [1].

В отличие от выражения (5.5) амплитуда сферической волны (5.6) уменьшается при удалении от источника как 1/r (мощность – как 1/r²), что связано с тем, что мощность изотропного источника распределяется по расходящимся сферам (4.10).

Таким образом, даже при отсутствии потерь в пространстве плотность потока мощности сферической волны уменьшается с расстоянием как 1/r².

На большом расстоянии от источника ЭМВ (в дальней зоне антенны) сферический волновой фронт в области приемной антенны можно аппроксимировать плоскостью, подобно тому, как земную поверхность считают плоской при малых высотах и на дистанциях, много меньших расстояния прямой видимости.

Плоская ЭМВ – идеализированная волна, имеющая плоский фазовый фронт (z = const), у которой существуют две взаимно перпендикулярные составляющие 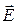и , зависящие только от координаты z и расположенные в плоскости, перпендикулярной z. ЭМВ называется однородной, если ее амплитуда постоянна во всех точках фазового фронта, и неоднородной, если ее амплитуда зависит от координат точек фазового фронта.

В дальнейшем будем считать, что направление распространения ЭМВ совпадает с осью z. Уравнения Максвелла в комплексной форме для составляющих векторов плоской волны в ДСК имеют вид

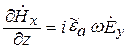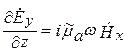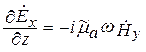; ; ; . (5.7)

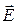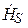Из формул (5.7) следует, что и взаимно перпендикулярны. (Это можно доказать, рассмотрев скалярное произведение векторов [11].) В дальнейшем будем обозначать координаты этих векторов и 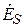, подчеркивая их поперечную направленность и расположение в плоскости x0y.

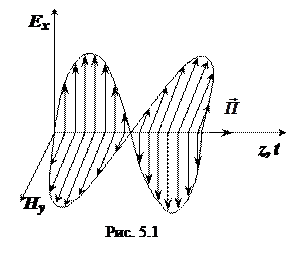Зная или 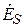, можно легко найти другую поперечную составляющую и перейти к обычным координатам (, , , ).

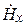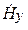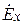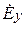Вектор Пойнтинга в данном случае имеет только продольную составляющую 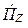(рис. 5.1). Решение уравнений (5.3) имеет вид

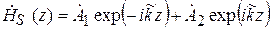. (5.8)

Первое слагаемое выражения (5.8) соответствует прямой волне, второе слагаемое – обратная волна, 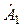и 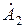– комплексные амплитуды данных бегущих волн (для 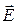– аналогично). Подставляя выражение (5.8) в (5.7), получим

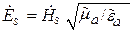. (5.9)

Запишем связь волнового числа (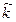) с комплексным коэффициентом распространения (g) для среды без магнитных потерь:

, (5.10)

Уравнение плоской волны с учетом (5.10) можно записать в виде

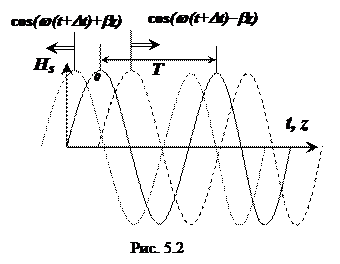
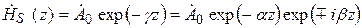. (5.11)

Для мгновенных значений из выражения (5.11) получаем

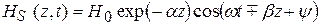. (5.12)

Направление распространения ЭМВ можно определить из анализа зависимости полной фазы (5.12) 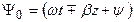от времени. Зафиксировав волновой фронт в какой-то момент времени, получаем, что если , то в следующий момент времени ЭМВ сместится в положительном направлении оси z, а при 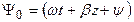волновой фронт будет двигаться в отрицательном направлении оси z (рис. 5.2) [1].

Из анализа формул (5.10)–(5.12) очевидно, что a – это коэффициент затухания, а b – коэффициент фазы.

Подставляя формулу (5.12) в (5.1), после решения уравнений относительно a и b получаем

, (5.13)

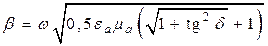. (5.14)

Множитель 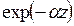в выражениях (5.10)–(5.12) показывает затухание при распространении ЭМВ вдоль оси z. Чем больше a, тем больше затухание.

Ослаблением (A) ЭМВ по полю называют величину (A_P = A² – ослабление ЭМВ по мощности)

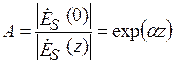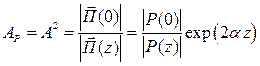, . (5.15)

На практике часто используют ослабление в децибелах (дБ):

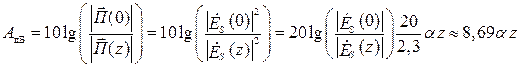. (5.16)

С ослаблением непосредственно связана глубина проникновения ЭМП в вещество (D° ), называемая также толщиной поверхностного слоя (скин-слоя, но это понятие логичнее использовать для металлов):

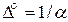. (5.17)

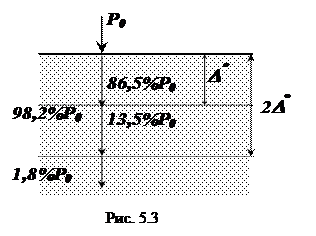При прохождении слоя вещества z =D° амплитуда ЭМП ослабляется в е (е = 2,718…) раз, и соответственно в следующий слой (рис. 5.3) проходит лишь 1/е² мощности ЭМП. Получается, что в поверхностном слое D° концентрируется 86,5% энергии ЭМП, в слое 2D° – 98,2%, а в слое 3D° – 99,8%.

Таким образом, зная коэффициент затухания, можно определить область преимущественной концентрации энергии ЭМВ в веществе.

В случае диэлектриков толщина поверхностного слоя значительна, в то время как для проводников на ВЧ и ОВЧ она составляет доли миллиметра [1].

Параметры ЭМВ. Длиной волны l называется расстояние между двумя фронтами ЭМВ, различающимися по фазе на 2p (360°):

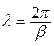. (5.18)

Фазовой скоростью v_ф называется скорость перемещения фазового (волнового) фронта ЭМВ. При анализе выражения (5.12) ранее были определены направление движения и скорость фронта ЭМВ

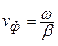. (5.19)

Фазовая скорость может изменяться в любых пределах (может быть больше с!), поскольку не является скоростью переноса энергии [1].

Групповой скоростью v_гр называют скорость движения фронта (например, максимума) огибающеймодулированного сигнала.

Информационный сигнал не является монохроматическим, он занимает полосу частот. Каждая спектральная составляющая может иметь свою скорость распространения, что в диспергирующих средах приводит к искажениям сигнала.

Понятие «групповая скорость» вводится для сред с малыми потерями, поэтому при Dw << w₀ можно записать [1]:

,

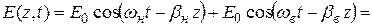
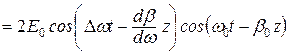где первый множитель описывает огибающую суммарного сигнала (биений), а второй – высокочастотное заполнение с циклической частотой несущей (w₀).

Для бигармонического сигнала получается наглядное представление (рис. 5.4). Таким образом, для узкополосного сигнала [1, 2]

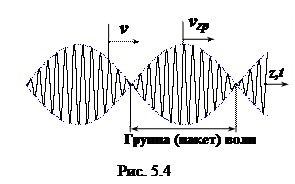
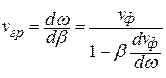. (5.20)

Для неискаженной передачи необходимо, чтобы групповая скорость была неизменной в полосе частот, занимаемой сигналом.

При отсутствии дисперсии 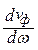= 0, и v_гр = v_ф; при нормальной дисперсии v_гр < v_ф ( 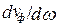< 0), а при аномальной дисперсии v_гр > v_ф ( 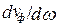>0).

При Dw/w₀ ® 0 период огибающей стремится в бесконечность, понятие «группа волн» распространяется на весь сигнал, и в итоге v_гр ® v_Э.

Групповая скорость узкополосного сигнала – это скорость передачи энергии, она не может быть выше скорости света.

Характеристическое сопротивление (Z_с) [41] ЭМВ равно отношению амплитуд поперечных составляющих электрического и магнитного полей

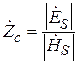. (5.21)

При комплексном Z_с отстает или опережает по фазе вектор 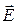на некоторый угол. На рис. 5.5 вектор опережает 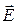на 90° (π/4), а на рис. 5.1 данные векторы синфазны.

Определим характеристическое сопротивление плоской волны. Пусть 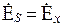, а , тогда из формул (5.7) следует:

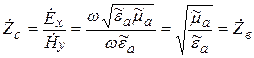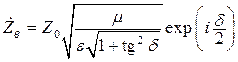, . (5.22)

Получается, что характеристическое сопротивление [41] зависит только от параметров среды. Z_в называют волновым сопротивлением среды. Следует отметить, что стандартом [41] рекомендуется термин «характеристическое сопротивление». Для ЭМВ, распространяющейся в некоторой среде, Z_c = Z_в.

Волновое сопротивление вакуума Z₀ (s = 0, e = m = 1):

377,0 Ом. (5.23)

Тогда выражение (5.22) можно записать в виде

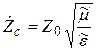. (5.24)

Список рекомендуемой литературы: [ 1, гл. 6–7, с. 30–38; 2, с. 50–56; 3, гл. 6–7, с. 27–34; 4, с. 26–33; 5, с. 26–30; 6, с. 116–123, 128–142, 198–205; 7, с. 67–82, 250–259; 8, с. 62–68; 9, с. 69–74; 10, с. 68–73; 11, с. 67–69, 130–139; 12, с. 182–194; 13, с. 140–149, 174–177, 187–190; 15, с. 302–307].

Контрольные вопросы и задания

1. Почему рассматриваемые в этой теме уравнения называются волновыми?

2. Чем волна отличается от колебания?

3. Чем отличаются волновые уравнения Д’Аламбера и Гельмгольца?

4. Следует ли из волновых уравнений независимость электрической и магнитной составляющих ЭМП?

5. Можно ли считать свет ЭМ волной?

6. Какие упрощения возможны в волновых уравнениях для сред без потерь?

7. Можно ли по виду электрической или магнитной составляющей плоской ЭМВ определить расположение другой составляющей ЭМП и направление распространения ЭМВ?

8. При каких условиях волновые уравнения для векторов 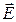и 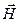идентичны?

9. Каково простейшее решение системы уравнений Максвелла?

10. Дайте определение волнового фронта.

11. Почему плотность потока энергии сферической волны уменьшается при удалении от источника даже в пространстве без потерь?

12. Какие упрощения в анализе ЭМП дает понятие «плоская волна»? В каких практических случаях допустимо ЭМВ считать плоской?

13. Чем отличаются однородные и неоднородные плоские волны?

14. Дайте определение коэффициентам затухания и фазы плоской ЭМВ.

15. Чем отличается волновое число k от g?

16. Какова пространственная структура плоской ЭМВ?

17. Как определить направление распространения ЭМВ?

18. Как с помощью понятия толщины поверхностного слоя можно оценить область преимущественной концентрации ЭМП?

19. Дайте определение основным характеристикам ЭМВ.

20. Чем групповая скорость отличается от фазовой?

21. Может ли фазовая скорость иметь бесконечное значение?

22. Чем волновое сопротивление отличается от характеристического?

23. Является ли групповая скорость скоростью передачи энергии?

24. Что такое дисперсия? Приведите примеры дисперсионных сред.

25. Укажите условие неискаженной передачи сигнала.

26. Чем нормальная дисперсия отличается от аномальной?

Date: 2015-06-11; view: 534; Нарушение авторских прав