Уравнение движения и режимы работы механизмов

Воспользуемся известной формулой об изменении кинетической энергии, которая применительно к вращающему звену приведения формулируется так: дифференциал кинетической энергии вращаю­щейся массы d T равен алгебраической сумме элементарных работ приведенных моментов d A _д = M _п.д dφ и d A _с = M _п._cdφ, т. е.

d T = d А = (М _п.д − М _п.с)dφ = M _п dφ. (1.25)

Интегрированием уравнения (1.25) в пределах от φ_о до φ

Т φ

∫ d T = ∫ M _пdφ = A,

^Т_о ^φ_о

получаем уравнение движения механизма в форме закона об измене­нии кинетической энергии:

_φ

Т − Т ₀ = J _п ω² /2 – J _п0 ω ₀² /2 = ∫ М _п dφ = А, (1.26)

^φ_о

_{φ φ φ}

где А = А _д − А _с или ∫ М _пdφ = ∫ М _п._д − ∫ М _п._сdφ −

^φ_о ^φ_о ^φ_о

суммарная работа приведенных моментов за время, соответствующее изменению обобщенной координаты от φ_о до φ.

Запишем уравнение (1.25) в несколько другом виде:

d = (J _п ω ²/2) = M _п dφ или (d /dφ) (J _п ω ²/2) = M _п. (1.27)

Дифференцированием (J _{п =} ω²/2) как функции двух независимых переменных (J _п и ω) находим уравнение движения механизма в диф­ференциальной форме:

J _п ω 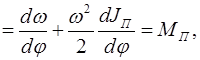или 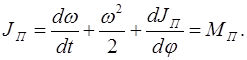(1.28)

С помощью уравнения (1.26) можно определить условия, необхо­димые для осуществления трех режимов работы механизмов: разбега, выбега и установившегося движения (рисунок 1.31). Представим (ус­ловно) левую часть уравнения (1.26), т. е. приращение кинетической энергии звена приведения, как работу сил инерции (отрицательную при ускоренном движении и положительную при замедленном), тогда уравнение (1.26) можно ин­терпретировать как урав­нение энергетического ба­ланса − соотношение ра­бот или мощностей всех сил, действующих на меха­низм в данном положении:

А _д − А _с ± А _и = 0. (1.29)

При разбеге механизма (ускоренное движение) ра­бота сил инерции, так же как и сил сопротивления, отрицательна, поэтому уравнение (1.29) принимает вид

А _д − А _с = А _и > 0 или А _д > А _с. (1.30)

При выбеге (замедленное движение), наоборот, работа сил инер­ции положительна, поэтому

А _д − А _с = − А _и < 0 или А _д < А _с . (1.31)

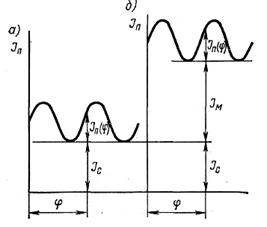Рисунок 1.30

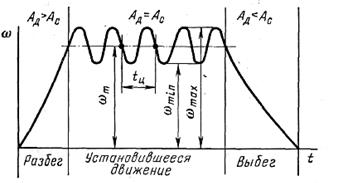Рисунок 1.31

При установившемся движении кинетическая энергия, равно как и угловая скорость звена приведения, изменяется (периодически) только в пределах цикла (рисунок 1.31), за весь же цикл или за период t = kt _ц (t _ц − время одного цикла, k − целое число циклов) среднее значение кинетической энергии Т _m остается постоянным, а ее прира­щение ∆ Т _m = 0 и соответствующая работа сил инерции А _и = 0. В этом случае

А _д − А _с = 0 или А _д = А _с. (1.32)

Полученные соотношения работ движущих сил и сил сопротив­ления являются необходимыми условиями работы механизма в режи­мах разбега, выбега и установившегося движения соответственно.

В режиме установившегося движения работают многие техно­логические и энергетические машины (например, металлорежущие станки, электрические генераторы). Работа же многих приборов и автоматических систем совершается во время разбегов (в течение времени срабатывания), чередующихся с выбегами.

Date: 2015-07-11; view: 416; Нарушение авторских прав