Приведение масс и сил. Звено приведения

Динамический анализ механизмов

Приведение масс и сил. Звено приведения

В динамике механизмов изучается их движение с учетом действующих сил.

Если все приложенные к звеньям силы известны, то можно определить закон движения какого-либо звена и механизма. Однако практическое решение этой задачи оказывается весьма сложным. Поэтому, как правило, прибегают к отдельным частным решениям, применяя способы приближенного определения движения механизма. Для этого сложный многозвенный механизм заменяют его динамической моделью. Если механизм имеет только одну степень свободы, то в качестве модели механизма принимают одно условное звено. Так, для системы «электродвигатель - исполнительный механизм» выбирают в качестве начального звена вал электродвигателя. Закон движения условного звена должен полностью совпадать с законом движения начального звена. При этом угловые скорости начального и условного звеньев должны быть равны.

При решении задач кинематики и силового расчета механизмов с одной степенью свободы угловая скорость ω₁ ведущего кривошипа принимают постоянной. В действительности ω₁ даже при устано­вившемся движении только в редких случаях остается постоянной. Обычно угловая скорость ω₁ периодически изменяется в зависимости от соотношения заданных сил, которые сами являются функциями различных параметров. Действительный закон движения ведущего звена определяют по методу Лагранжа с помощью звена приведения (динамической модели механизма), в качестве которого чаще всего выбирают ведущее звено - кривошип (или ползун). Если, например, задан шарнирный четырехзвенник с одной степенью свободы

(рисунок 1.29, а), то его ведущий криво­шип 1 становится динамической моделью механизма (рисунок 1.29, б) после приведения к нему всех движущихся масс и всех заданных сил: движущих и сопротивления. Иначе говоря, для обращения кри­вошипа в звено приведения его момент инерции J _l должен быть за­менен приведенным моментом инерции J _п так, чтобы кинетическая энергия звена приведения Т _п стала равной кинетической энергии все­го механизма (Σ Т_i), т. е.

Т _п = J _пω₁² / 2 = Σ [ J_Si ω _i ² / 2 + m _iυ ² _Si / 2]. (1.20)

Кроме того, мощности приведенных моментов сил сопротивлений N _п.с и движущих сил N _п.д должны быть равны сумме мощностей всех сил и моментов сил сопротивлений (F _сi, M _ci) и движущих (F _дi, М _дi), действующих на звенья механизма, т. е.

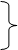N _п.с= M _п.сω₁ = Σ N_ci = Σ [ M_ci ω _i + F_ci υ _ci cos α _ci ]; (1.21)

N _п.д = M _п.дω₁ = Σ N _дi = Σ [ М _дi ω _i + _дi υ_дi cos α _{д i} ].

В выражениях (1.20) и (1.21) для i -го звена: υ_Si и ω _i - скорость центра масс и угловая скорость; m_i и J_Si - масса и момент инерции звена относительно оси, перпендикулярной плоскости вращения и проходящей через ц. м.; M_ci и М_дi - моменты пар сил сопротив­лений и движущих; F_ci и υ_ci - сила сопротивлений и скорость точки C_i ее приложения; a_ci - угол, образуемый векторами F_ci и υ_{c i} (аналогично, α_дi = F _дi υ _дi).

Приведение масс и сил может производиться не только к звену, но и к его произвольно взятой точке А (рисунок 1.29, в) - точке приве­дения. В этом случае в качестве обобщенной координаты выбирают перемещение S_a точки А по окружности. Массы всех подвижных звеньев заменяют приведенной массой т _п, сосредоточенной в точке А, а все заданные силы и моменты сил - приведенной силой F _п, при­ложенной к той же точке. Изложение материала данной главы про­изводится для случая, когда звеном приведения является ведущий кривошип. Если приведение масс и сил производится к точке, то формулы приведения и другие закономерности определяются ана­логично.

Из уравнения (1.20) находим приведенный момент инерции звена приведения:

J _п = 2 Т _{п /} ω²₁ = Σ [ J_Si (ω_i /ω₁)² + m_i (υ_Si /ω _i)² ]; (1.22)

он является функцией квадратов передаточных отношений. Послед­ние зависят от φ, поэтому и приведенный момент инерции является функцией обобщенной координаты J _п = J _п(φ).

Если ведущий кривошип 1 статически уравновешен

(рисунок 1.29, б), то _n

υ _S1 = 0 и J _п = J _{1 +} Σ [ J _Si (ω_i ⁄ω₁)² + m _i (υ _Si /ω₁)²],

^{i =2}

где J ₁ = const - момент инер­ции кривошипа относительно оси его вращения.

Если в механизме имеются еще k звеньев, связанных с ве­дущим кривошипом постоянны­ми передаточными отношения­ми (ω _i /ω_ı = const) _n-k

J _п = J _с + Σ [ J _Si (ω _i /ω₁)² + m _i (υ_Si /ω₁)²] = J _с + J _п (φ), (1.23)

^{i= 1}

_k

где J _с = J ₁+Σ J s_j (ω _j /ω₁)² − постоянная часть приведенного момента

ⁱ⁼¹

инерции, а J _п (φ) - переменная (рисунок 1.30).

Если все звенья механизма (например, зубчатого) вращаются вокруг своих центральных осей, то υ _S = 0, ω_i /ω_{1 =} const, J _п(φ) = 0 и J _п = J _c = const.

Решением уравнений (1.21) относительно приведенных моментов сил сопротивлений и сил движущих находим следующие зависимости, выражающие закон передачи сил и моментов (без учета сил трения):

М_п.с = Σ[М_c.i(ω_i /ω₁) + F _c.i(v_ci /ω₁)cosα_ci]; (1.24)

М_п.д = Σ[М_д.i(ω_i /ω₁) + F _д.i(v_дi /ω₁)cosα_дi].

Date: 2015-07-11; view: 787; Нарушение авторских прав