
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Тема 9. Теоретико-игровые модели принятия решений
|
|
На практике часто возникают ситуации, в которых сталкиваются интересы двух и более сторон. Такие ситуации называются конфликтными. Наиболее типичны конфликтные ситуации при планировании военных действий, в спорте, в рыночной экономике. Однако и некоторые задачи планирования и управления производством могут быть отнесены к конфликтным (например, обоснование цены на оборудование, планирование уровня качества и т.д.). В конфликтных ситуациях выбор решения зависит не только от нас, но и от образа действий (поведения) противоборствующей стороны.
Конфликтные ситуации изучаются "теорией игр ". Игра при этом представляет упрощенную модель конфликтной ситуации. Теория игр позволяет математически обосновать рекомендации по рациональному образу действий конфликтующих сторон (называемых иногда игроками).
Игры подразделяются на парные, когда сталкиваются интересы двух сторон, и множественные, когда участников конфликта несколько. Наиболее изучены парные игры.
Игра как модель конфликтной ситуации отличается от нее четко сформулированными правилами, включающими:
- возможные варианты поведения сторон;
- объем информации о поведении противоборствующих сторон;
- результат конфликта (игры) в зависимости от действий (ходов) сторон.
При этом полагается, что интересы участников конфликта могут быть оценены количественно.
Если в результате игры одна из сторон выигрывает столько, сколько проигрывает другая, то такие игры называются играми с нулевой суммой (сумма выигрыша равна нулю).
Ходом в теории игр называется выбор одного из возможных по правилам варианта действий и его осуществление.
Ходы бывают личные и случайные. Личный ход осуществляется по выбору игрока, а случайный - на основании какого-либо механизма случайного выбора. В теории игр исследуются конфликтные ситуации, в которых поведение выбирается только самими участниками (т.е. игра содержит только личные ходы).
Очень важным в теории игр является понятие стратегии. Стратегией называется совокупность правил, по которым осуществляется выбор варианта действий в любой возможной ситуации, т.е. стратегия определена, если выбраны личные ходы для любой ситуации. Хотя решения принимаются по ходу игры, стратегия может быть выбрана заранее.
В зависимости от количества возможных стратегий игры делятся на конечные и бесконечные. Теория игр даст правила построения оптимальных стратегий.
Оптимальной называется стратегия, обеспечивающая максимально возможный средний выигрыш при многократном повторении игры. В теории игр оптимальные стратегии вырабатываются без учета возможных ошибок противника.
Наиболее простой является парная игра с нулевой суммой. Но с ее помощью хорошо описывается большинство конфликтных ситуаций.
Рассмотрим парную игру. Сторона А может выбрать m стратегий (i=1,2,...,m), а сторона В - n стратегией (j=1, 2,...,n ). Если сторона А выбрала определенную i - ю стратегию, а сторона В -j-ю стратегию, то выбор стратегий однозначно определяет исход игры - a, выигрыш (положительный или отрицательный) стороны А. Известные значения для любой пары стратегий составляют платежную матрицу игры или просто матрицу игры.
Строки матрицы соответствуют стратегиям игрока А, а столбцы - стратегиям игрока В. Элемент матрицы aij показывает выигрыш игрока А, если он избрал стратегию i, а игрок В- стратегию j.
| Стратегии | B1 | B2 | … | Bj | … | Bn |
| A1 | a11 | a12 | … | a1j | … | a1n |
| A2 | a21 | a22 | … | a2j | … | a2n |
| … | … | … | … | … | … | |
| Ai | ai1 | ai2 | … | ajj | … | ain |
| … | … | … | … | … | … | … |
| Am | am1 | am2 | … | amj | … | amn |
Исходя из предположения о разумности противников, определим стратегии игроков.
Проанализируем последовательно стратегии игрока А (строки платежной матрицы). При выборе стратегии необходимо учитывать, что игрок В ответит стратегией, при которой наш выигрыш минимален. Найдем минимальный выигрыш для каждой из стратегий:
| ai=min aij (i=1, 2,.., n). j |
Числа ai (минимумы по строкам) указываются обычно рядом с матрицей в виде добавочного столбца. Таким образом, выбор стратегии Аi обеспечивает нам выигрыш αi. Естественно, что необходимо выбрать такую стратегию, при которой наш выигрыш максимален
a = max ai,
i
или a=max min aij,
i j
Величина a называется нижней ценой игры. Она показывает минимально гарантированный выигрыш игрока А. Стратегия Аi, обеспечивающая выигрыш a, называется максиминной. Нижнюю цену игры называют также максимальным выигрышем или максимином.
Аналогичные рассуждения можно провести и за игрока В, который стремится обратить выигрыш игрока А в минимум. Поэтому, просмотрев нее столбцы, выделим в каждом из них максимальное значение выигрыша aij.:
b=max aij .
i
Значения b пишутся внизу матрицы в виде дополнительной строки.
| Игроки | B1 | B2 | … | Bj | … | Bn an1 an2 … | ai … anm b |
| A1 | a11 | a12 | … | a1j | … | a1n | a1 |
| A2 | a12 | a22 | … | a2j | … | a2n | a2 |
| … | … | … | … | … | … | … | |
| Ai | ai1 | ai2 | … | ajj | … | ain | ai |
| … | … | … | … | … | … | … | … |
| Am | am1 | am2 | … | amj | … | amn | am |
| bj | b1 | b2 | … | bj | … | bn |
Игрок В выбирает такую стратегию Вj, при которой минимизируется значение b=min max aij.
j i
Величина b называется верхней ценой игры, или минимаксным выигрышем (минимаксом). Стратегия Вj, дающая выигрыш b, называется минимаксной. Придерживаясь этой стратегии, игрок В не проиграет более величины b. Нижнюю и верхнюю цены игры мы определяли, исходя из предположения о разумности игроков. Этот принцип выбора стратегий называется принципом минимакса.
| II | В1 | В2 | В3 |
| А1 | |||
| А2 | |||
| А3 |
Задача 8. Найти верхнюю и нижнюю цены игр, платежные матрицы которых приведены в таблицах.
| I | В1 | В2 | В3 |
| А1 | |||
| А2 | |||
| А3 |
Методические указания к решению
Определим минимумы строк ai, и максимумы столбцов bj (т.е. соответственно минимальные выигрыши игрока А и максимальные проигрыши игрока В). Для игры, матрица которой задана таблицей I, результаты приведены в таблице:
| I | В1 | В2 | В3 | ai |
| А1 | ||||
| А2 | ||||
| А3 | ||||
| bj |
Максимальное значение ai,.равное 4, дает нижнюю цену игры.
Верхняя цена игры (равная минимуму bj) составляет 11.
Для второй игры получим таблицу:
| II | В1 | В2 | В3 | ai |
| А1 | ||||
| А2 | ||||
| А3 | ||||
| bj |
В данном случае нижняя и верхняя цены игры равны 8, т.е. max ai, = min bj или max min aij = min max aij= g.
Общее значение верхней и нижней цены игры, равное g, называется чистой ценой игры, а игры, имеющие чистую цену, называются играми с седловой точкой.
Решение игры заключается в выборе стратегии поведения каждого игрока. Оптимальной для каждого игрока является стратегия, обеспечивающая ему при многократном повторении игры максимально возможный средний выигрыш (или минимально возможный средний проигрыш).
Наиболее просто находится решение игры, имеющей седловую точку. Седловой точке соответствуют оптимальные (соответственно максиминная и минимаксная) стратегии каждого игрока. При этом, если один из игроков придерживается своей оптимальной стратегии, то для другого невыгодно отклоняться от своей оптимальной стратегии. В этом случае выигрыш постоянен и равен чистой цене игры g. Так как чистая цена игры соответствует максимину, то отклонение игрока А от стратегии, дающей этот выигрыш, приведет только к его уменьшению.
Аналогичная картина наблюдается и у игрока В. Таким образом, в играх с седловой точкой оптимальные стратегии обладают устойчивостью, т.е. каждому игроку выгодно применять какую-либо чистую стратегию, определяемую принципом минимакса.
Однако на практике часто встречаются игры, у которых верхняя и нижняя цены не равны. Если в этом случае применять только одну чистую стратегию по принципу минимакса, то выигрыш игрока А не будет превышать a, а выигрыш игрока В - b.
В случае отсутствия седловой точки выигрыш каждого игрока может быть увеличен, если применять не одну, а несколько стратегий.
Такие стратегии называют смешанными и заключаются они в случайном чередовании чистых стратегий.
Смешанная стратегия SA игрока А определяется набором вероятностей р1,р2,…,рm использования чистых стратегий Аi (i=1,2,…,m), причем 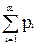 =1.
=1.
Аналогично, для игрока В смешанная стратегия игрока SВ определяется набором вероятностей q1,q2,…,qn использования чистых стратегий Bj (j=1,2,…n), и 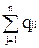 =1.
=1.
Согласно основной теореме теории игр, каждая игра имеет, по крайней мере, одно решение в области смешанных стратегий. При этом чистые стратегии могут рассматриваться как частный случай смешанных.
Пара оптимальных стратегий S*А и S*В обладает следующим свойством: если один игрок придерживается своей оптимальной стратегии, то другому не выгодно отклоняться от своей оптимальной.
Цена игры g при применении смешанных стратегий находится в пределах между верхней и нижней ценами игры: a£ g £ b
Применение игроком А своей оптимальной стратегии S*А при любой стратегии противника Вj обеспечивает ему выигрыш не менее g, т.е.
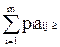 g (j=1,2,…,n). (9.1)
g (j=1,2,…,n). (9.1)
Аналогично, для игрока В использование оптимальной стратегии S*В обеспечит ему при любой стратегии противника А выигрыш не больше g, т.е.
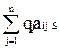 g (i=1,2,…,m). (9.2)
g (i=1,2,…,m). (9.2)
Соотношения (1) и (2) используются для решения игры. Ее сводят к решению задачи линейного программирования. Предварительно анализируют матрицу, исключают из нее дублирующие и невыгодные стратегии.
При определении оптимальной стратегии игрока А должны выполняться условия:
 р1а11+р2а21+ …+рiаi1+….+рmаm1³g
р1а11+р2а21+ …+рiаi1+….+рmаm1³g
 р1а12+р2а22+ …+рiаi2+….+рmаm2³g
р1а12+р2а22+ …+рiаi2+….+рmаm2³g
…………………………………….
р1а1j+р2а2j+ …+рiаij+….+рmаmj³g
……………………………………
р1а1n+р2а2n+ …+рiаin+….+рmаmn³g
Цена игры g, если элементы платежной матрицы неотрицательны - всегда положительное число. Если в матрице есть отрицательные элементы, ее можно преобразовать, прибавляя ко всем элементам определенное положительное число.
Систему ограничений (3) можно преобразовать, разделив на g все члены неравенства и обозначив рi/g=xi.
В результате получим
 а11x1+а21x2+ …+аi1xi+….+аm1xm³1
а11x1+а21x2+ …+аi1xi+….+аm1xm³1
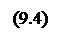 а12x1+а22x2+ …+аi2xi+….+аm2xm³1
а12x1+а22x2+ …+аi2xi+….+аm2xm³1
…………………………………….
а1jx1+а2jx2+ …+аijxi+….+аmjxm³1
……………………………………
а1nx1+а2nx2+ …+аinxi+….+аmnxm³1
Из условия 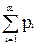 =1 получим:
=1 получим:
x1+x2+…+xi+…+xm=1/g (9.5)
Оптимальная стратегия S*А должна максимизировать значение g, а следовательно, минимизировать 1/g.
Таким образом, задача определения выбора вероятностей pi составляющих оптимальную стратегию S*А, сводится к минимизации линейной формы (5) при ограничениях (4).
Решив полученную задачу линейного программирования и найдя величины xi и 1/g, определим значения рi=gxi.
Оптимальная стратегия игрока В -S*В находится аналогичным образом, исходя из условия минимизации проигрыша (g), при соблюдении условий (9.2).
Разделив систему неравенств (2) на g и заменив qi на yi =qi /g, получим следующую задачу линейного программирования:
 а11y1+а12y2+ …+а1jyj+….+а1nyn£1
а11y1+а12y2+ …+а1jyj+….+а1nyn£1
а21y1+а22y2+ …+а2jyj+….+а2nyn£1
 …………………………………….
…………………………………….
аi1y1+аi2y2+ …+аijyj+….+аjnyn £1
……………………………………
аm1y1+аm2y2+ …+аmjyj+….+аmnyn£1
y1+y2+…+yj+…+yn®max
Задача максимизации линейной формы при ограничениях (9.6) является двойственной по отношению к задаче, определяемой условиями (9.4) и (9.5).
Таким образом, задача отыскания решения матричной игры сводится к решению пары симметричных двойственных задач линейного программирования. Решение прямой задачи дает оптимальную стратегию игрока A (S*А), а двойственной - оптимальную стратегию игрока В (S*В).
Задача 9.1. Найти оптимальные стратегии игроков А и В, т.е. решение игры, платежная матрица которой представлена первой таблицей задачи 8.
Методические указания к решению
Найдем смешанную стратегию игрока А.
Обозначив x1= p1/g, x2= p2/g, x3= p3/g, получим следующую модель задачи:
L=x1+x2+x3 ® min,
 9x1+4x2+11x3£1
9x1+4x2+11x3£1
4x1+11x2+2x3£1
11x1+2x2+13x3£1
xi ³ 0
Решая эту задачу симплекс-методом, получим:
x1= 1/28, x2=1/14, x3 = 1/28.
Цена игры g=1/Lmin , g= 1/(1/28+1/14+1/28)=7.
Соответственно, вероятности использования игроком А первой, второй и третьей стратегий составят:
р1=gx1= 7*1/28=1/4
р2=gx2= 7*1/14=1/2
р3=gx3= 7*1/28=1/4,
т.е.
S*А =(1/4,1/2,1/4).
Оптимальная стратегия игрока В (S*В) находится аналогичным образом, только ограничения типа (£) составляются по строкам, а критерий оптимальности следует не минимизировать, а максимизировать. Составив модель и решив ее, получим, что оптимальная стратегия игрока В состоит в следующем:
q1=1/4
q2=1/2
q3=1/4,
т.е.
S*B =(1/4,1/2,1/4).
В рассмотренной игре каждый игрок использует все свои стратегии, т.е. все стратегии здесь активны. (Активной называется стратегия, вероятность использования которой больше нуля). Сведение игры к задаче линейного программирования позволяет получить точное ее решение. Однако в ряде задач достаточно иметь приближенное решение, обеспечивающее выигрыш, близкий к цене игры. Поэтому, учитывая, что для больших матриц применение линейного программирования не самый простой путь решения, используют различные приближенные методы (итерационные, например).
Задание. Найти оптимальные стратегии игроков А и В, т.е. решение игры, платежная матрица которой представлена таблицей:
| Стратегии | В1 | В2 | В3 | В4 | В5 |
| А1 | |||||
| А2 | |||||
| А3 | |||||
| А4 |
Date: 2015-06-11; view: 1307; Нарушение авторских прав