Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Законы распределения случайной величины, описывающие безотказность, ремонтопригодность, долговечность и сохраняемость
|
|
При распределении Вейбулла-Гнеденко вероятность безотказной работы (БР) на интервале (0,1) имеет вид (см. рисунок). Вероятность безотказной работы равна:
.
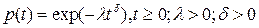Из этого выражения следует, что плотность наработки на отказ равна:
 .
|
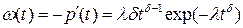Среднее время безотказной работы (наработка на отказ), согласно выражению:
 ,
|
где Г – полная гамма-функция.
Закон Вейбулла-Гнеденко проявляется в модели так называемого "слабого звена". Если система состоит из группы независимых элементов, отказ или неисправность которых приводит к отказу всей системы, то вероятность ее безотказной работы определяется предельным отклонением.
Например, ресурс подшипника качения ограничивается одним из элементов (шарик или ролик, конкретный участок сепаратора) и описывается указанным распределением.
Кроме того, в расчетной практике широкое распространение получили два однопараметрических распределения, которые являются частными случаями распределения Вейбулла. Это экспоненциальное распределение (при постоянном коэффициенте вариации V = 1) и распределение Релея (при постоянном коэффициенте вариации V = 0,523).
Экспоненциальный закон не учитывает постепенного изменения параметров технического состояния, например, в результате изнашивания, старения и т. д, а рассматривает так называемые нестареющие элементы и их отказы. Наибольшее распространение получил при описании внезапных отказов, продолжительности ремонтных воздействий и т. д.
;
;
.
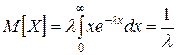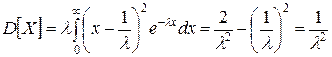Вероятность безотказной работы для экспоненциального закона:
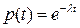, t³ 0; l> 0.
При распределении Релея вероятность безотказной работы на интервале (0, t) равна:
 .
|
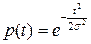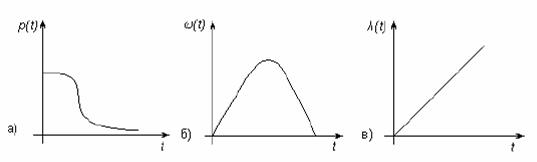
где: s – параметр распределения Релея, который одновременно является модой этого распределения.
Мода непрерывного распределения есть точка максимума плотности распределения вероятности w(t). Мода дискретного распределения есть такое спектральное значение, при котором предшествующие и последующие спектральные значения имеют вероятности, меньшие, чем Р(t).
Плотность распределения наработки на отказ равна:
 .
|
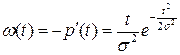Интенсивность отказов равна:
 .
|
Среднее время безотказной работы – (математическое ожидание) для распределения Релея равно:
 .
|
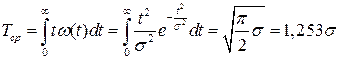Соответственно дисперсия времени БР:
 .
|
|
В теории надежности для «стареющих» элементов в качестве распределения интервала безотказной работы наряду с распределением Вейбулла при d> 1 используют нормальное распределение.
Изменение технического состояния осуществляется по нормальному закону – когда на протекание исследуемого процесса и его результат влияет сравнительно большое число независимых (или слабозависимых) факторов, каждый из которых, в отдельности, оказывает лишь незначительное действие по сравнению с суммарным влиянием всех остальных.
 .
|
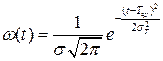Это распределение зависит от двух параметров: среднего времени Тср и дисперсии безотказной работы 
.
Логарифмически нормальный (логнормальный) закон может встречаться, если на протекание исследуемого процесса и его результат влияет сравнительно большое число случайных и взаимонезависимых факторов, интенсивность действия которых зависит от достигнутого случайной величиной состояния. Это так называемая модель пропорционального эффекта.
Date: 2015-06-11; view: 752; Нарушение авторских прав