Скорость упругих волн

Стержень называется «тонким», когда его поперечные размеры малы по сравнению с длиной упругой волны 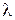. При малых продольных деформациях стержня справедлив закон Гука, устанавливающий пропорциональность между величиной относительной продольной деформации 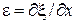и величиной напряжения (Н/м²):

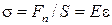(27.24)

Где 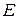– модуль Юнга (Па). Каждая из величин σ и ε является алгебраической и их знаки всегда одинаковы (при растяжении – положительны, при сжатии отрицательны).

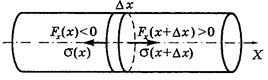Процесс распространения упругой продольной волны в стержне означает распространение в нем локальных продольных деформаций растяжения и сжатия, которые испытывают последовательно все элементы стержня. Рассмотрим малый элемент стержня в тот момент прохождения волны, когда он оказался растянутым.

Согласно второму закону Ньютона

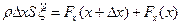(27.25)

Здесь

В рассматриваемый момент 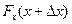> 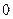и < 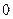. Соответствующие значения напряжений σ и деформаций ε в обоих крайних сечениях выделенного элемента ( 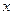и ) – положительны (поскольку отвечают растяжению). Поэтому правую часть уравнения можно записать в виде

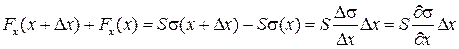
Тогда уравнения движения (25) после сокращения на величину элементарного объема 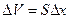примет вид 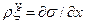. Учитывая закон Гука (24), окончательно получаем:

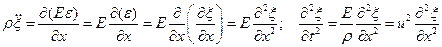(27.26)

Мы пришли к волновому уравнению, в котором скорость распространения волны определяется величиной

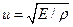(27.27)

Полученное выражение для фазовой скорости продольной упругой волны справедливо только в приближении тонкого стержня. Для не тонкого стержня выражение для u имеет место более сложный вид и значение u оказывается больше, чем в случае тонкого стержня.

Скорость поперечных волн упругих волн в неограниченной изотропной твердой среде

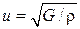(27.28)

где G – модуль сдвига среды, ρ – ее плотность.

Скорость поперечной волны в гибком шнуре (струне).

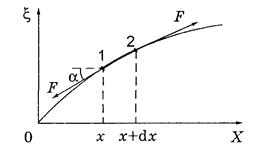В состоянии равновесия натянутая струна проходит вдоль оси абсцисс. Отклонения точек струны от состояния равновесия будем описывать функцией 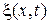. Найдем уравнение малых поперечных колебаний натянутого шнура, исходя из основного равнения динамики.

Рассмотрим малый участок струны«1,2», концы которого имеют координаты 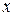и . Длина этого участка равна

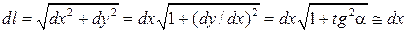(27.29)

Мы воспользовались тем обстоятельством, что колебания струны достаточно малые, так что угол наклона к оси 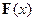любого элемента струны пренебрежимо мал.

В силу малости искривления струны величину вызванного ей удлинения можно считать постоянной вдоль всей струны и неизменной во времени. Тогда величину силы натяжения 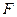также можно считать неизменной во времени и вдоль струны.

Разложим силы натяжения 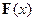и 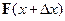, действующие на выделенный элемент струны, на составляющие вдоль оси 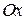и ортогонально ей. Суммарная сила натяжения вдоль оси абсцисс:

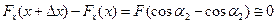
Для ортогональный составляющих:

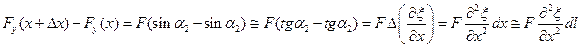
Уравнение Ньютона для выделенного элемента шнура плотности 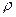и площадью поперечного сечения :

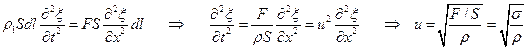(27.30)

Здесь 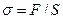- напряжение в шнуре. Сравнивая формул (30) с выражениями для скорости (27),(28), видим, что скорость поперечной волны в упругом шнуре отличается от скорости упругой волны в тонком стрежне заменой модулей упругости 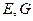на величину напряжения .

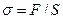Date: 2015-06-11; view: 1775; Нарушение авторских прав