Упругие волны в безграничной среде

ЛЕКЦИЯ 27 -2011

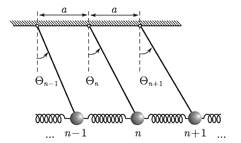
Упругой волной называют процесс распространения состояния возмущения в упругой среде. При этом происходит именно процесс распространения состояния возмущения частиц среды (т.е. их отклонения от равновесного, недеформированного состояния), но сами частицы испытывают периодическое движение около своих положений равновесия. По своей сути волна – это колебательный процесс в протяженной среде.

Существует достаточно много типов классификации волн:

По размерности:

· Одномерные

· Двумерные

· Трехмерные

По форме поверхности постоянной фазы (волновой поверхности):

· Плоские

· Сферические

· Цилиндрические

По направлению смешения колебаний относительно направления распространения волны

· Продольные

· Поперечные

По зависимости от времени

· Монохроматические

· Немонохроматические

Несмотря на большое разнообразие физических процессов, вызывающих волны, их образование происходит по общему принципу. Возмущение, произошедшее в какой-либо точке среды в некоторый момент времени, проявляется спустя определенное время на интересующем нас расстоянии от исходной точки, т.е. передается с определенной скоростью.

Бегущие волны. Пусть в некоторый момент времени функция, характеризующая отклонение от состояния равновесия отдельных точек среды имеет вид, представленный на рисунке:

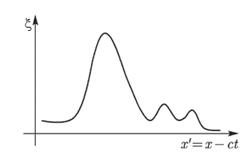Пусть с течением времени вид этой функции не меняется, а происходит лишь смещение ее вдоль среды. Это означает, что в системе, связанной с волной, в которой координата каждой точки среды есть , мы имеем функцию . Пусть волна движется с постоянной скоростью вдоль оси 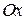лабораторной системе. Координаты и 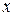одной и той же точки в собственной и лабораторной системе связаны соотношением: . Поэтому бегущая волна может быть представлена в виде:

(27.1)

Волна, распространяющаяся в отрицательной направление оси 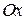, имеет вид:

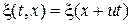. (27.2)

В частном случае, когда мы получаем гармоническую волну

(27.3)

Обозначая

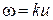, (27.4)

перепишем гармоническую волну в виде:

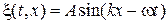(27.5)

Величина 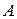называется амплитудой волны, а функция

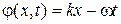(27.6)

фазой волны. Зафиксировав точку 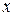, мы получаем гармоническое колебаний с циклической частотой . Согласно (6), в любых двух точках, отстоящих на расстояние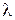

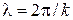, (27.7)

отклонение 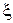от положения равновесия одинаково в любой момент времени.

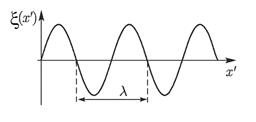Иными словами, точки, находящиеся на расстоянии друг от друга, равном 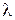, колеблются одинаково, синхронно. Величина 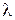называется длиной волны, а число 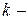волновым числом.

Рисунок 2. Гармоническая волна в собственной системе отсчета.

При учете затухания в линейной среде амплитуда волны уменьшается с расстоянием по экспоненциальному закону

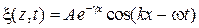(27.8)

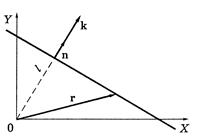Обобщим выражение для волны, на случай когда она распространяется в произвольном направлении, не обязательно совпадающем с осью 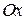. Пусть направление распространения волны определяет единичный вектор 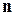. Профиль волны задается функцией 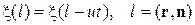. Для гармонической волны введем волновой вектор :

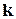(27.9)

Воспользовавшись формулой (4), выражение для гармонической волны можно представить в виде:

(27.10)

Если наблюдатель движется вдоль направления распространения волны со скоростью 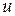, то он регистрирует одну и ту же фазу волны: 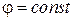. Поэтому скорость 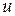называют фазовой скоростью.

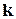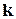Заметим, что в отличие от волнового вектора , фазовая скорость u не является вектором: в любом направлении, составляющим заданный угол с волновым вектором , скорость перемещения данной фазы (данного состояния колебания частиц) равна (а не , как должно быть, если бы скорость являлась вектором). В частности, фазовые скорости распространения волны вдоль координатных осей 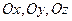равны, соответственно: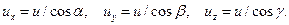

Волна вида (10) называется плоской волной, поскольку в трехмерном пространстве геометрическим место точек, отвечающим в данный момент времени одинаковому значению фазы 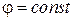, является плоскость ортогональная направлению распространения волны .

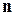При распространении волны в линейной поглощающей среде выражение для гармонической волны, распространяющейся в направлении 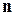, имеет вид

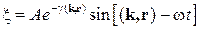(27.11)

Date: 2015-06-11; view: 582; Нарушение авторских прав