
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Приклади
|
|
1. Знайти інтервали зростання і спадання функції 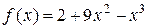 .
.
Розв’язання. Використаємо достатню умову зростання (спадання) функції.
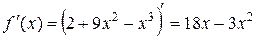 .
.
Розв’язавши нерівність 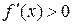 , знайдемо інтервали зростання функції f:
, знайдемо інтервали зростання функції f:
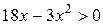 Û
Û 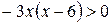 Û
Û 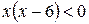 Û
Û 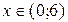 .
. 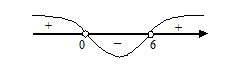
Отже, 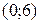 – інтервал зростання функції f.
– інтервал зростання функції f.
Знайдемо інтервали спадання функції f. Для цього потрібно розв’язати нерівність 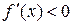 .
.
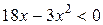 Û
Û 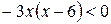 Û
Û 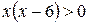 Û
Û 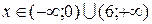 .
.
Отже, 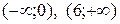 – інтервали спадання функції f.
– інтервали спадання функції f.
2. Знайти інтервали зростання і спадання функції, точки екстремуму і екстремуми функції f:
а) 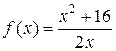 ; б)
; б) 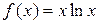 .
.
Розв’язання. Використаємо алгоритм знаходження інтервалів зростання і спадання, точок екстремуму і екстремумів функції.
а) 1. Областю визначення функції f є множина R \{0}. Зобразимо її на числовій прямій (рис.4.9).
2. Знайдемо  :
:
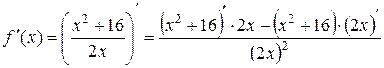 =
= 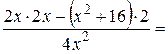
= 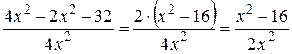 .
.
3. Знайдемо критичні точки функції f.
 =0 Û
=0 Û 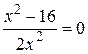 Û
Û 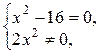 Û
Û 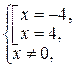 Û
Û 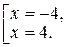
Оскільки точки х =–4 і х =4 належать області визначення функції f, то вони є критичними точками цієї функції.
У точці х =0 похідна  =¥. Але ця точка не належить D (f), а тому не є критичною точкою функції f.
=¥. Але ця точка не належить D (f), а тому не є критичною точкою функції f.
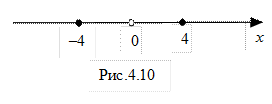
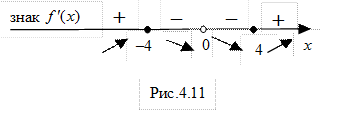
Позначимо знайдені критичні точки х =–4 і х =4 на числовій прямій (рис.4.10). У результаті утворяться (–¥;–4), (–4;0), (0;4) (4;+¥), на кожному з яких  зберігає сталий знак.
зберігає сталий знак.
4. Визначимо знак  на кожному з утворених інтервалів. Для цього необхідно обчислити значення
на кожному з утворених інтервалів. Для цього необхідно обчислити значення  у будь-якій одній точці з кожного інтервалу.
у будь-якій одній точці з кожного інтервалу.
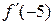 =
= 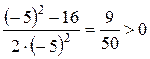 ;
; 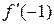 =
= 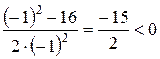 ;
;
 =
= 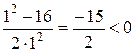 ;
; 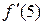 =
= 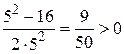 .
.
Отже, 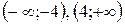 – інтервали зростання функції f;
– інтервали зростання функції f; 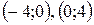 – інтервали спадання функції f.
– інтервали спадання функції f.
5. Оскільки при переході через критичну точку х =–4 похідна  змінює знак з “+” на “–”, то ця точка є точкою максимуму функції f, тобто
змінює знак з “+” на “–”, то ця точка є точкою максимуму функції f, тобто 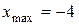 . При переході через критичну точку х =4 похідна
. При переході через критичну точку х =4 похідна  змінює знак з “–” на “+”. Тому ця точка є точкою мінімуму функції f, тобто
змінює знак з “–” на “+”. Тому ця точка є точкою мінімуму функції f, тобто 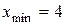 .
.
6. Знайдемо екстремуми функції f:
 ;
;
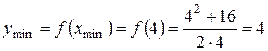 .
.
Критичні точки х =–4 і х =4 є стаціонарними точками функції f (бо в цих точках 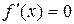 . Тому з’ясувати, чи будуть вони точками екстремуму функції f можна за допомогою похідної другого порядку
. Тому з’ясувати, чи будуть вони точками екстремуму функції f можна за допомогою похідної другого порядку 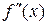 .
.
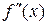 =
= 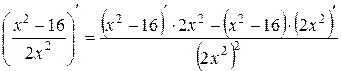 =
=
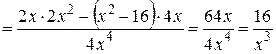 .
.
Оскільки 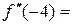
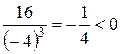 , то х =–4 – точка максимуму функції f.
, то х =–4 – точка максимуму функції f. 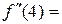
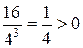 , тому х =4 – точка мінімуму функції f.
, тому х =4 – точка мінімуму функції f.
б) 1. Оскільки функція 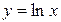 визначена на множині додатних чисел, то областю визначення функції
визначена на множині додатних чисел, то областю визначення функції 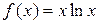 є інтервал
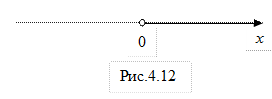
є інтервал 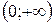 . Зобразимо його на числовій прямій (рис.4.12).
. Зобразимо його на числовій прямій (рис.4.12).
2. 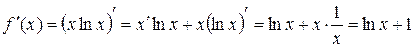 .
.
3. Знайдемо критичні точки функції f.
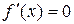 Û
Û 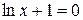 Û
Û 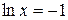 Û
Û 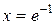 Û
Û 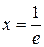 .
.
Оскільки точка 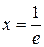 належить області визначення функції f, то вона є критичною точкою цієї функції. Інших критичних точок функція f не має. Позначимо знайдену критичну точку на числовій прямій. (рис.4.13). У результаті утворяться
належить області визначення функції f, то вона є критичною точкою цієї функції. Інших критичних точок функція f не має. Позначимо знайдену критичну точку на числовій прямій. (рис.4.13). У результаті утворяться 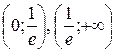
4. Визначимо знак  на кожному з утворених інтервалів:
на кожному з утворених інтервалів:
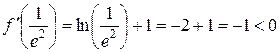 ;
;
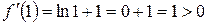 .
.
Отже, 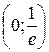 – інтервал спадання,
– інтервал спадання, 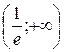 – інтервал зростання функції f.
– інтервал зростання функції f.
5. Оскільки при переході через критичну точку 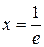 похідна
похідна  змінює знак з “–” на “+”, то ця точка є точкою мінімуму функції f, тобто
змінює знак з “–” на “+”, то ця точка є точкою мінімуму функції f, тобто 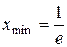 .
.
6. 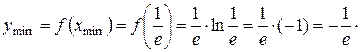
3. Знайти найбільше і найменше значення функції 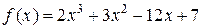 на відрізку [0;2].
на відрізку [0;2].
Розв’язання. Функція f є неперервною на R, а, отже, і на відрізку [0;2]. Використаємо алгоритм знаходження найменшого і найбільшого значень функції на відрізку.
1. D (f)= R.
2. 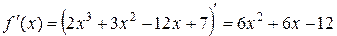 .
.
3. Знайдемо критичні точки функції f.
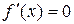 Û
Û 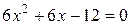 Û
Û 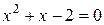 Û
Û 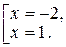
Оскільки точки х =–2 і х =1 належать D (f), то вони є критичними точками функції f. Однак інтервалу (0;2) належить лише точка х =1.
4. Обчислимо значення функції f у критичній точці х =1 та на кінцях відрізка [0;2]:
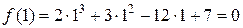 ;
; 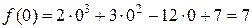 ;
;
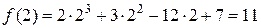 .
.
5. Серед знайдених значень виберемо найбільше і найменше.
Отже,  ,
, 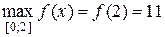 .
.
Таким чином, функція f найменше значення набуває всередині відрізка [0;2] (точці х =1), а найбільше – на кінці цього відрізка (у точці х =2).
4. Бурова вишка розташована в полі на відстані 9 км від найближчої точки шосе. З бурової потрібно направити кур’єра у населений пункт, розташований на відстані 15 км від згаданої точки (шосе вважаємо прямою лінією). Швидкість кур’єра на велосипеді полем дорівнює 8 км / год, а вздовж шосе – 10 км / год. До якої точки шосе йому потрібно їхати, щоб за найменший час дістатися до населеного пункту?
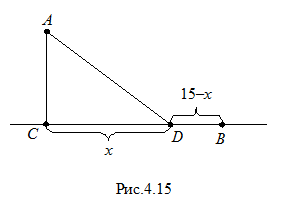 Розв’язання. Нехай точка А – бурова вишка, В – населений пункт, що знаходиться на шосе, АС – відстань від бурової вишки до найближчої точки шосе, АС =9 км, СВ =15 км (рис.4.15).
Розв’язання. Нехай точка А – бурова вишка, В – населений пункт, що знаходиться на шосе, АС – відстань від бурової вишки до найближчої точки шосе, АС =9 км, СВ =15 км (рис.4.15).
Нехай D – точка шосе, до якої потрібно їхати кур’єру, щоб за найменший час дістатися до населеного пункту. Її положення визначає відстань від неї або до населеного пункту (точка В), або до точки С. Нехай СD = х. Тоді DВ =15– х. Визначимо час, який затратить кур’єр на рух полем (відрізок АD) і вздовж шосе (відрізок DВ).
З прямокутного трикутника АСD за теоремою Піфагора маємо:
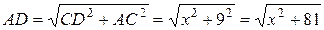 .
.
Час, затрачений на рух полем, дорівнює 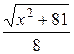 , в здовж шосе –
, в здовж шосе – 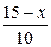 . Загальний час, затрачений на всю подорож, є таким:
. Загальний час, затрачений на всю подорож, є таким:
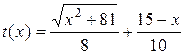 .
.
З умови задачі випливає, що х Î[0,15].
Отже, завдання полягає в знаходженні найменшого значення функції 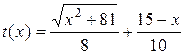 на відрізку [0,15].
на відрізку [0,15].
Використаємо алгоритм знаходження найменшого і найбільшого значень функції на відрізку.
1. D (t)= R.
2. 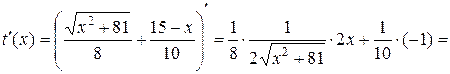
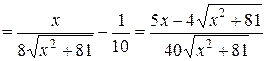 .
.
3. Знайдемо критичні точки функції t (x).
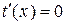 Û
Û 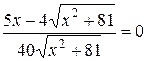 Û
Û 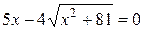 Û
Û
Û 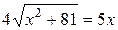 Û
Û 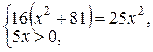 Û
Û 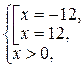 Û х =12.
Û х =12.
Оскільки точка х =12 належить D (t), то вона є критичною точкою функції 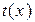 . Ця ж точка належить інтервалу (0;15).
. Ця ж точка належить інтервалу (0;15).
4. Обчислимо значення функції 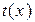 у критичній точці х =12 та на кінцях відрізка [0;15]:
у критичній точці х =12 та на кінцях відрізка [0;15]:
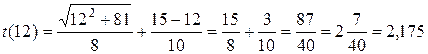 ;
;
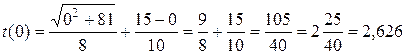 ;
;
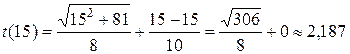 .
.
5. Серед знайдених значень вибираємо найменше:
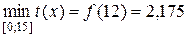 .
.
Отже, для того щоб за найменший час дістатися до населеного пункту, кур’єр повинен їхати у точку шосе, яка знаходиться на відстані 12 км від точки С і 3 км від населеного пункту (точки В). При цьому на всю подорож ним буде затрачений мінімальний час – 2,175 години.
5. У цеху підприємства виготовляють продукцію одного виду. Витрати на виробництво х одиниць продукції виражаються функцією 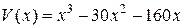 (грн.), а дохід, одержаний від її реалізації (загальна вартість продукції), функцією
(грн.), а дохід, одержаний від її реалізації (загальна вартість продукції), функцією 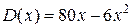 (грн.). Визначити, яку кількість продукції потрібно виготовити, щоб прибуток був максимальним.
(грн.). Визначити, яку кількість продукції потрібно виготовити, щоб прибуток був максимальним.
Розв’язання. Відомо, що прибуток 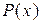 від реалізації х одиниць товару визначається як різниця між доходом і витратами, тобто
від реалізації х одиниць товару визначається як різниця між доходом і витратами, тобто
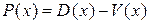 =
= 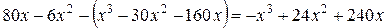 .
.
За змістом задачі х Î[0;+¥).
Отже, потрібно знайти найбільше значення функції 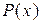 =
= 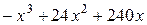 на проміжку [0;+¥).
на проміжку [0;+¥).
1. D (P)= R.
2. 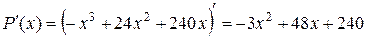 .
.
3. Знайдемо критичні точки функції 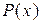 .
.
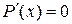 Û
Û 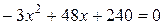 Û
Û 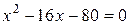 Û
Û 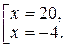
Оскільки точки х =20 і х =–4 належать D (P), то вони є критичними точками функції 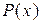 . Проміжку [0;+¥) належить лише точка х =20.
. Проміжку [0;+¥) належить лише точка х =20.
4. Обчислимо значення функції 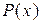 у критичній точці х =20, у точці х =0 та знайдемо границю функції
у критичній точці х =20, у точці х =0 та знайдемо границю функції 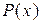 , коли х ®+¥:
, коли х ®+¥:
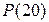 =
= 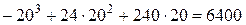 ;
;
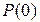 =
= 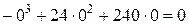 ;
;
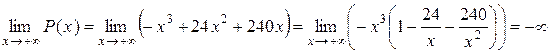 .
.
5. Отже, 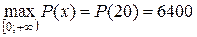 .
.
Таким чином, щоб мати максимальний прибуток, у цеху підприємства потрібно виготовляти 20 одиниць продукції. При цьому максимальний прибуток становитиме 6400 грн.
6. Знайти інтервали опуклості вгору, опуклості вниз та точки перегину графіка функції f:
а) 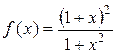 ; б)
; б) 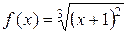 .
.
Розв’язання. Використаємо алгоритм знаходження інтервалів опуклості вгору, опуклості вниз і точок перегину графіка функції.
а) 1. D (f)= R. Зобразимо область визначення на числовій прямій (рис.4.16).

2) Знайдемо  . Спочатку знайдемо
. Спочатку знайдемо  :
:

= 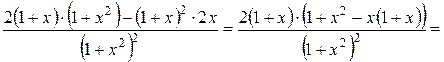
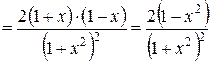 .
.
Тоді
 =
= 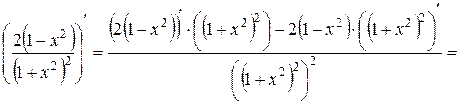
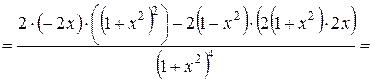
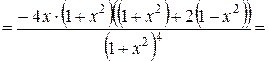
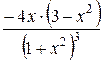 .
.
3. Знайдемо критичні точки другого роду функції f:
 =0 Û
=0 Û 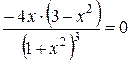 Û
Û 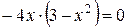 Û
Û 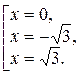
Оскільки точки 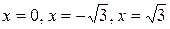 належать області визначення функції f, то вони є критичними точками другого роду цієї функції.
належать області визначення функції f, то вони є критичними точками другого роду цієї функції.
Точок, в яких  =¥ або
=¥ або  не існує, не має.
не існує, не має.
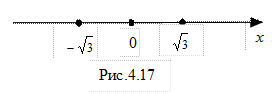
Позначимо знайдені критичні точки другого роду на числовій прямій (рис.4.17).
4. Визначимо знак  на кожному з утворених інтервалів:
на кожному з утворених інтервалів:
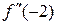 =
= 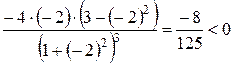 ;
;
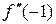 =
= 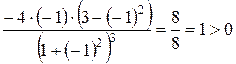 ;
;
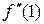 =
= 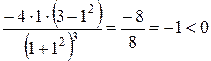 ;
;
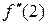 =
= 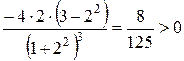 .
.
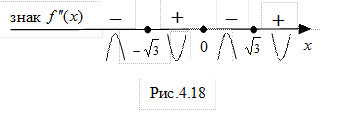
Оскільки 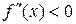 на інтервалах
на інтервалах 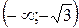 і
і 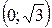 , то ці інтервали є інтервалами опуклості вгору графіка функції f.
, то ці інтервали є інтервалами опуклості вгору графіка функції f.
 на інтервалах
на інтервалах 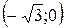 і
і 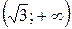 . Тому ці інтервали є інтервалами опуклості вниз графіка функції f.
. Тому ці інтервали є інтервалами опуклості вниз графіка функції f.
5. Оскільки при переході через кожну з критичних точок другого роду 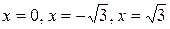 похідна другого порядку
похідна другого порядку  змінює знак, то кожна з цих точок є точкою перегину графіка функції f.
змінює знак, то кожна з цих точок є точкою перегину графіка функції f.
б) 1. D (f)= R. Зобразимо область визначення на числовій прямій (рис.4.19).

2. Знайдемо похідні першого і другого порядків функції f:
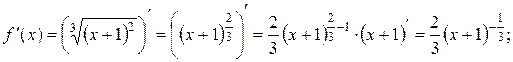
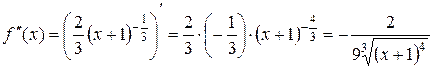 .
.
3. Знайдемо критичні точки другого роду функції f:
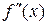 =0 Û
=0 Û 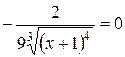 Û х ÎÆ,
Û х ÎÆ,
тобто точок, в яких  =0, не має.
=0, не має.
У точці х =–1 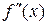 =¥. Оскільки ця точка належить D (f), то вона є критичною точкою другого роду функції f. Точок, в яких
=¥. Оскільки ця точка належить D (f), то вона є критичною точкою другого роду функції f. Точок, в яких  не існує, не має.
не існує, не має.
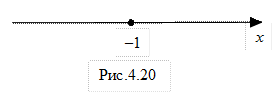
Позначимо знайдену критичну точку другого роду на числовій прямій (рис.4.20).
4. Визначимо знак  на кожному з утворених інтервалів:
на кожному з утворених інтервалів:
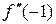 =
= 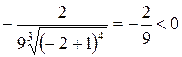 ;
; 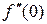 =
= 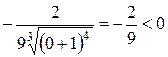 .
.
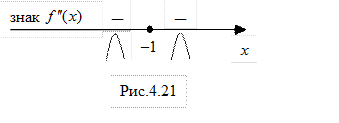
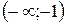 і
і 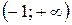 – інтервалами опуклості вгору графіка функції f (бо на цих інтервалах
– інтервалами опуклості вгору графіка функції f (бо на цих інтервалах 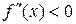 )
)
5. Критична точка другого роду х =–1 не є точкою перегину графіка функції f, оскільки при переході через цю точку  не змінює знаку.
не змінює знаку.
7. Знайти асимптоти графіка функції f:
а) 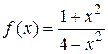 ; б)
; б) 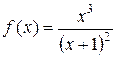 ; в)
; в) 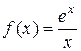 ; г)
; г) 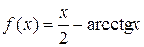 .
.
Розв’язання.
а) Оскільки 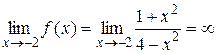 ,
, 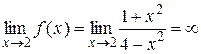 , то прямі х =–2 і х =2 – вертикальні асимптоти графіка функції f.
, то прямі х =–2 і х =2 – вертикальні асимптоти графіка функції f.
Знайдемо невертикальні асимптоти (похилі, горизонтальні):
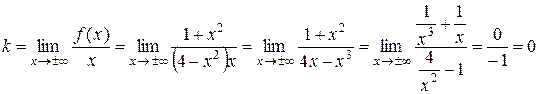 ;
;
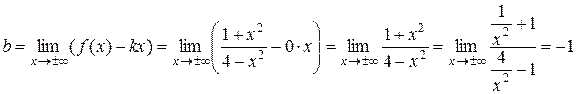 .
.
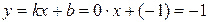 .
.
Отже, y =–1 – горизонтальна асимптота графіка функції f.
б) Оскільки 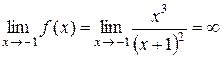 , то пряма х =–1 – вертикальна асимптота графіка функції f.
, то пряма х =–1 – вертикальна асимптота графіка функції f.
Знайдемо невертикальні асимптоти:
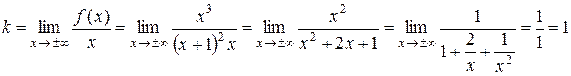 ;
;
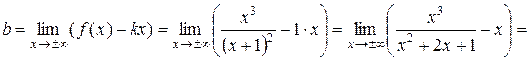
= 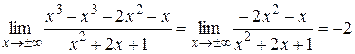 .
.
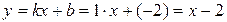 .
.
Отже, 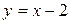 – похила асимптота графіка функції f.
– похила асимптота графіка функції f.
в) 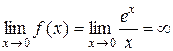 . Тому х =0 – вертикальна асимптота графіка функції f.
. Тому х =0 – вертикальна асимптота графіка функції f.
Знайдемо невертикальні асимптоти. Оскільки
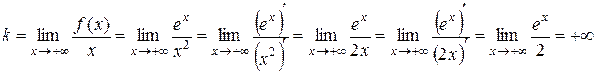 ,
,
то правої похилої асимптоти графік функції f не має (при знаходженні границі двічі використано правило Лопіталя).
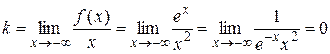 (бо
(бо 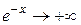 і
і 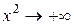 , коли
, коли 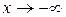 );
);
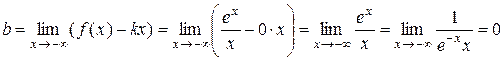 .
.
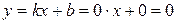 .
.
Отже, y =0 – ліва горизонтальна асимптота графіка функції f.
г) Оскільки задана функція неперервна на множина R усіх дійсних чисел, то її графік вертикальних асимптот не має.
Знайдемо невертикальні асимптоти.
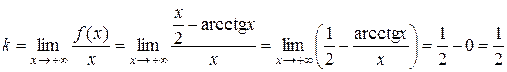
(бо arcctg x ®0, коли x ®+¥).
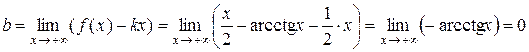 .
.
Отже, 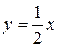 – права похила асимптота графіка функції f.
– права похила асимптота графіка функції f.
Розглянемо випадок, коли x ®–¥:
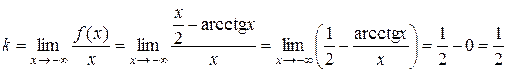
(бо arcctg x ®p, коли x ®–¥).
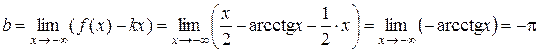 .
.
Отже, 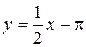 – ліва похила асимптота графіка функції f.
– ліва похила асимптота графіка функції f.
Завдання для самостійного розв’язування
2. Знайти інтервали зростання і спадання функції f:
а) 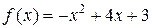 ; в)
; в) 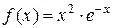 .
.
3. Знайти точки екстремуму і екстремуми функції f:
1) 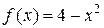 ; 2)
; 2) 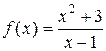 ; 3)
; 3) 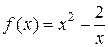 ;
;
4) 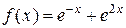 ; 5)
; 5) 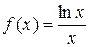 .
.
4. Знайти найбільше і найменше значення функції f на вказаному відрізку:
а) 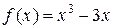 , [0;2]; г)
, [0;2]; г) 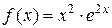 , [–2;1].
, [–2;1].
5. Парканом завдовжки 200 м необхідно загородити найбільшу за площею прямокутну ділянку. Якими мають бути розміри ділянки?
6. Для перевезення овочів необхідно виготовити ящики без кришок, що мають форму прямокутного паралелепіпеда. Об’єм кожного ящика дорівнює 40,5 дм 3, а висота – 2 дм. Якими повинні бути розміри основи ящика, щоб на його виготовлення було витрачено найменшу кількість матеріалу?
7. У одному з цехів підприємства виготовляють продукцію певного виду. Витрати на виробництво х одиниць продукції виражаються функцією 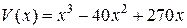 (грн.), а дохід, одержаний від її реалізації – функцією
(грн.), а дохід, одержаний від її реалізації – функцією 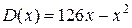 (грн.). Визначити, яку кількість продукції потрібно виготовити, щоб прибуток від її реалізації був максимальним.
(грн.). Визначити, яку кількість продукції потрібно виготовити, щоб прибуток від її реалізації був максимальним.
8. Знайти інтервали опуклості вгору, опуклості вниз та точки перегину графіка функції f:
а) 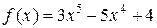 ; б)
; б) 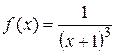 ; в)
; в) 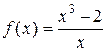 ;
;
г) 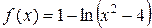 .
.
9. Знайти асимптоти графіка функції f:
а) 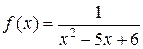 ; б)
; б) 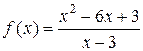 ; в)
; в) 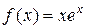 ;
;
е) 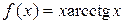 .
.
Відповіді:
2. а) інтервал зростання: (–¥; 2), інтервал спадання: (2; +¥); в) інтервали зростання: (–¥; –2) і (0; +¥), інтервал спадання: (–2; 0).
3. 1) xmax =0, ymax =4; 2) xmax =–1, ymax =–2, xmin =3, ymin =6; 3) xmin =–1, ymin =3; 4) xmin = 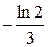 , ymin =
, ymin = 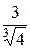 ; 5) xmax = e, ymax =
; 5) xmax = e, ymax = 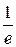 ;
;
4. а) 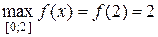 ,
, 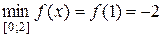 ; г)
; г) 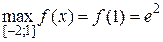 ,
, 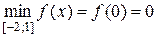 .
.
5. 50 м ´ 50 м.
6. 4,5 дм ´ 4,5 дм.
7. 24.
8. а) опукла вгору на інтервалі (–¥; 1) і опукла вниз на інтервалі (1; +¥), х =1 – точка перегину;
б) опукла вгору на інтервалі (–¥; –1) і опукла вниз на інтервалі (–1; +¥), точок перегину немає;
в) опукла вгору на інтервалі 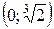 , опукла вниз на інтервалах: (–¥; 0) і
, опукла вниз на інтервалах: (–¥; 0) і 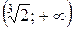 ,
, 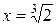 – точка перегину;
– точка перегину;
г) опукла вниз на інтервалах: (–¥; –2) і (2; +¥), інтервалів опуклості вгору і точок перегину немає.
9. а) х =2, х =3 – вертикальні асимптоти, y =0 – горизонтальна асимптота;
б) х =3 – вертикальна асимптота, y = х –3 – похила асимптота;
в) y =0 – ліва горизонтальна асимптота;
е) y =1 – права горизонтальна асимптота.
Date: 2015-07-02; view: 647; Нарушение авторских прав