Застосування похідної до дослідження функцій

Зростання і спадання функції. Інтервал (a; b) називають інтервалом зростання (спадання) функції y = f (x), якщо на цьому інтервалі функція f зростає (спадає), тоді як на будь-якому ширшому інтервалі вона вже не є зростаючою (не є спадною). Наприклад, для функція f (x)= х ² інтервал зростання – (0;+¥), а інтервал спадання – (–¥;0).

Знаходження інтервалів зростання і спадання за допомогою похідної грунтується на такій теоремі.

Достатня умова зростання (спадання) функції. Якщо 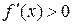(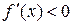) для всіх х з інтервалу (а; b), то на цьому інтервалі функція f зростає (спадає).

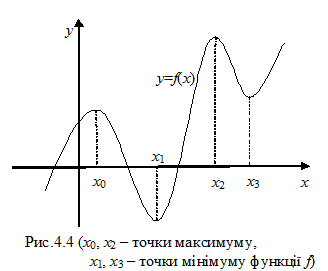Екстремуми функції. Точку х ₀ називають точкою максимуму (точкою мінімуму) функції y=f(x), якщо існує окіл цієї точки такий, що для всіх х з цього околу, крім х = х ₀, виконується нерівність f (x ₀)> f (x) (f (x ₀)< f (x)) (рис.4.4). Функція може мати декілька точок максимуму і мінімуму, а може не мати жодної.

Точки максимуму і точки мінімуму функції f називають точками екстремуму цієї функції.

Значення функції y = f (x) у точці максимуму (точці мінімуму) називають максимумом (мінімумом) функції f. Максимум і мінімум функції f називають екстремумами цієї функції.

Необхідна умова існування точки екстремуму функції (теорема Ферма). Якщо х ₀ – точка екстремуму функції f, то 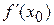=0 або функція f не є диференційованою у точці x ₀ ( 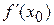=¥ або 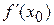не існує).

Точки з області визначення функції f, в яких дорівнює нулю або нескінченності, або не існує, називають критичними точками функції f.

Враховуючи це означення теорему Ферма можна сформулювати так: якщо х ₀ – точка екстремуму функції f, то ця точка є критичною точкою функції f.

Теорема Ферма стверджує, що точки екстремуму функції містяться серед її критичних точок. Але не кожна критична точка функції є точкою екстремуму цієї функції. Виділити точки екстремуму серед її критичних точок допомагає достатня умова існування точки екстремуму функції.

Достатня умова існування точки екстремуму функції. Нехай функція 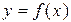диференційована в околі критичної точки x ₀, за винятком, можливо, самої точки x ₀, в якій функція f неперервна. Тоді: 1) якщо при переході точки x через точку x ₀ змінює знак з “+” на “–”, то точка x ₀ є точкою максимуму функції f, а якщо – з“–” на “+”, то точка x ₀ є точкою мінімуму функції f; 2) якщо при переході точки x через точку x ₀ не змінює знаку, то x ₀ не є точкою екстремуму функції f.

Алгоритм знаходження інтервалів зростання і спадання,

точок екстремуму і екстремумів функції y = f (x)

1. Знайти область визначення функції f і зобразити її на числовій прямій.

2. Знайти .

3. Знайти критичні точки функції f і позначити їх на числовій прямій. (Вони розіб’ють область визначення функції f на інтервали, на кожному з яких зберігає сталий знак.)

4. Визначити знак на кожному з утворених інтервалів. Для цього необхідно обчислити значення у будь-якій одній точці з кожного інтервалу. Інтервали, на яких 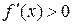є інтервалами зростання функції, а на яких 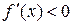– інтервалами спадання функції.

5. За характером зміни знаку при переході через критичні точки знайти точки екстремуму функції f: якщо при переході через критичну точку змінює знак з “–” на “+”, то ця точка є її точкою мінімуму; якщо змінює знак з “+” на “–”, то ця точка є її точкою максимуму; якщо не змінює знаку, то ця точка не є точкою екстремуму.

6. Обчисливши значення функції f в знайдених точках екстремуму, знайти екстремуми f.

Критичну точку x ₀ функції f, для якої 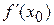=0, називають стаціонарною точкою функції f. З’ясувати, чи буде стаціонарна точка x ₀ функції f точкою екстремуму цієї функції, можна по іншому, а саме, використовуючи другу похідну функції f: якщо 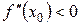, то x ₀ – точка максимуму, а якщо 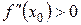, то x ₀ – точка мінімуму функції f.

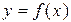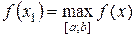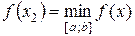Найбільше і найменше значення функції на відрізку. Якщо функція неперервна на відрізку [ a; b ], то за другою теоремою Вейєрштрасса вона набуває на цьому відрізку найменшого і найбільшого значень, тобто існують такі точки х ₁, х ₂Î[ a; b ], що і . Точки х ₁ і х ₂ можуть бути як внутрішніми точками відрізка [ a; b ] (але тоді вони обов’язково є точками екстремуму, а, отже, критичними точками функції f), так і його межовими точками (тобто кінцями відрізка [ a; b ]). Звідси випливає такий алгоритм знаходження найбільшого і найменшого значень функції f, неперервної на відрізку [ a; b ]:

1. Знайти область визначення функції f.

2. Знайти .

3. Знайти критичні точки функції f і відібрати ті з них, які належать інтервалу (а; b).

4. Обчислити значення функції f у відібраних критичних точках і на кінцях відрізка [ a; b ], тобто в точках x = a і x = b.

5. Серед знайдених значень функції f вибрати найбільше і найменше. Це будуть найбільше і найменше значення функції f на відрізку [ a; b ].

Опуклість графіка функції. Графік функції y = f (x) називають опуклим вгору (опуклим вниз) на інтервалі (a; b), якщо всі точки графіка, за виключенням точки дотику, розміщені нижче (вище) будь-якої дотичної, проведеної до графіка функції на цьому інтервалі (рис.4.5, рис.4.6).

Інтервал (a; b), на якому графік функції y = f (x) опуклий вгору (опуклий вниз), а на будь-якому ширшому інтервалі вже не є опуклим вгору (опуклим вниз), називають інтервалом опуклості вгору (опуклості вниз) графіка функції f.

Достатня умова опуклості вгору (опуклості вниз) графіка функції. Якщо 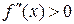(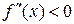) для всіх х з інтервалу (а; b), то на цьому інтервалі графік функція f опуклий вниз (опуклий вгору).

Точку х ₀ з області визначення функції, в якій змінюється характер опуклості графіка функції, називають точкою перегину графіка цієї функції (рис.4.7) У точках перегину дотична перетинає графік функції.

Точки з області визначення функції f, в яких дорівнює нулю або нескінченності, або не існує, називають критичними точками другого роду функції f.

Достатня умова існування точки перегину графіка функції. Якщо x ₀ – критична точка другого роду функції f і при переході через цю точку змінює знак, то x ₀ є точкою перегину графіка функції y = f (x). Якщо ж при переході через точку x ₀ не змінює знаку, то x ₀ не є точкою перегину графіка функції y = f (x).

Алгоритм знаходження інтервалів опуклості вгору,

опуклості вниз і точок перегину графіка функції y = f (x)

1. Знайти область визначення функції f і зобразити її на числовій прямій.

2. Знайти .

3. Знайти критичні точки другого роду функції f і позначити їх на числовій прямій. (Вони розіб’ють область визначення функції f на інтервали, на кожному з яких зберігає сталий знак.)

4. Визначити знак на кожному з утворених інтервалів. Для цього необхідно обчислити значення у будь-якій одній точці з кожного інтервалу. Інтервали, на яких 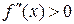, є інтервалами опуклості вниз, а на яких 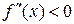– інтервалами опуклості вгору графіка функції f.

5. За характером зміни знаку при переході через критичні точки другого роду знайти точки перегину графіка функції f: якщо при переході через критичну точку другого роду змінює знак, то ця точка є точкою перегину, а якщо не змінює знаку, то ця точка не є точкою перегину графіка функції f.

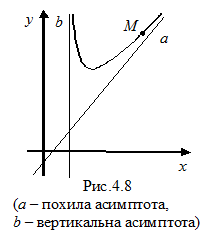Асимптоти графіка функції. Пряму а називають асимптотою графіка функції f, якщо відстань від довільної точки М графіка до прямої а прямує до нуля при необмеженому віддаленні точки М у нескінченність (рис.4.8).

Розрізняють три види асимптот: вертикальні, горизонтальні та похилі.

1. Якщо 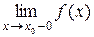=¥ або 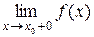=¥, або 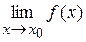=¥, то пряма х = х ₀ є вертикальною асимптотою графіка функції f.

2. Якщо 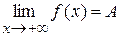(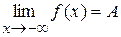), то пряма y = А є правою (лівою) горизонтальною асимптотою графіка функції f. Якщо 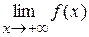= 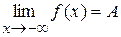, то пряма y = А є горизонтальною асимптотою графіка функції f.

3. Якщо існують скінченні границ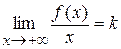і і 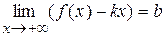(або ці ж границі при х ®–¥), то пряма y = kx + b є правою (лівою) похилою асимптотою графіка функції f. Якщо 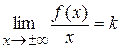і 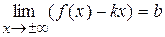, то пряма y = kx + b є похилою асимптотою графіка функції f.

Горизонтальну асимптоту можна одержати як частковий випадок похилої асимптоти при k =0.

Date: 2015-07-02; view: 942; Нарушение авторских прав