Понятие аналитической функции. Сопряженные гармонические функции

О: Однозначная функция w = 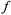(z) называется аналитической (регулярной, голоморфной) в т. 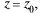если она дифферен-

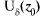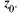цируема в некоторой окрестности точки Функция

w = 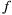(z) называется аналитической в области D если она аналитическая в каждой точке D.

Однозначные основные элементарные функции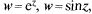

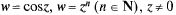являются аналитическими в Z 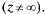Примером дифференцируемой, но не аналитической в точке функции является 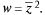Действительно,

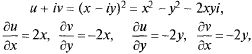
т.е. условия Коши—Римана выполняются для 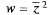только в

т. z = 0. Таким образом, она в этой точке дифференцируема, но не аналитическая.

Отметим, что аналитическая в D функция w = 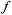(z) имеет в D производные любого порядка

Теорема Коши для односвязной области. Если D - односвязная ограниченная область, w = f (z) - аналитическая в этой области функция, то для любого кусочно-гладкого замкнутого контура L, лежащего в D, интеграл от f (z) по L равен нулю: .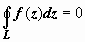
Доказательство. Удивительно, но эта важнейшая теорема непосредственно и просто следует из условий Коши-Римана и формулы Грина. Так как, по доказанному выше, 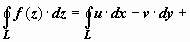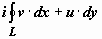, то, применяя к действительным криволинейным интегралам формулу Грина, получим 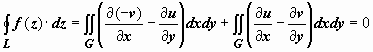вследствие условий Коши-Римана 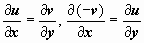. Символом G в доказательстве обозначена область, заключённая внутри контура L.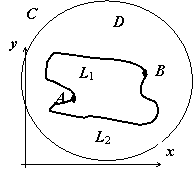
Следствие. Для всех кусочно-гладких кривых, лежащих внутри области D, в которой аналитична функция w = f (z), и имеющих общие начальную и конечную точки, интеграл 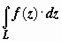имеет одинаковое значение.
Доказательство полностью повторяет доказательство Теоремы 1 раздела 16.3.3.5.1. Объединение L ₁∪ L ₂⁻ кривых - замкнутый контур, поэтому .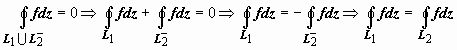
Оказывается, что справедлива и обратная теорема Морера: если функция w = f (z) непрерывна в односвязной области D и интеграл по любому замкнутому кусочно-гладкому контуру, лежащему в D, равен нулю, то функция аналитична в области D.

19.6.2.2. Теорема Коши для многосвязной области. Если функция w = f (z) аналитична в замкнутой многосвязной ограниченной области 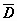, ограниченной контурами L ₀ (внешняя граница), L ₁, L ₂, …, L_k, то интеграл от f (z), взятый по полной границе области 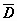, проходимой так, что область остаётся с одной стороны, равен нулю.
Доказательство и здесь воспроизводит доказательство формулы Грина для многосвязной области. Рассмотрим случай, когда граница области 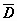(на рисунке область заштрихована) состоит из внешнего контура L ₀ и внутренних контуров L ₁ и L ₂. Соединим контур L ₀ разрезом FM с контуром L ₁, разрезом BG - с контуром L ₂. Область 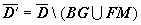с границей 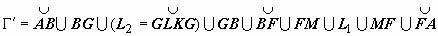односвязна, поэтому для неё справедлива интегральная теорема Коши: 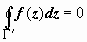. Интегралы по каждому из разрезов входят в этот общий интеграл дважды в противоположных направлениях и, как следствие, взаимно уничтожаются, поэтому остаются только интегралы по контурам, проходимым так, что область остаётся с одной стороны.
В дальнейшем нам понадобится другая формулировка этой теоремы. Буквами без верхнего индекса будем обозначать контуры, проходимые против часовой стрелки, с верхним минусом - по часовой. Мы доказали, что 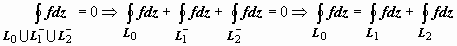. Таким образом, интеграл по внешнему контуру равен сумме интегралов по внутренним контурам, при этом все контуры обходятся в одном направлении.

Теорема Тейлора (о разложении функции в степенной ряд).

Функция, аналитическая в области комплексных чисел D, в окрестности каждой точки z ₀этой области представляется в виде степенного ряда:
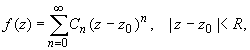(1)

радиус сходимости R которого не меньше, чем расстояние от точки z ₀ до границы области D.
Такой степенной ряд называется рядом Тейлора.

Коэффициенты ряда Тейлора вычисляются по формуле:

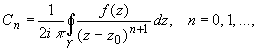(2)

где 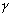- произвольный контур, принадлежащий области D и охватывающий точку z ₀ (в частности, 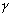- окружность 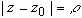), или по формуле:

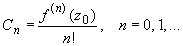(3)

Радиус сходимости ряда Тейлора равен расстоянию от точки z ₀ до ближайшей особой точки функции.

Для вычисления радиуса сходимости ряда Тейлора можно также использовать формулы:

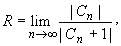
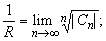
Основные разложения.

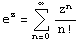(z принадлежит области комплексных чисел);

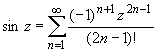(z принадлежит области комплексных чисел);

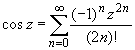(z принадлежит области комплексных чисел);

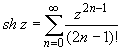(z принадлежит области комплексных чисел);

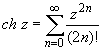(z принадлежит области комплексных чисел);

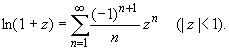
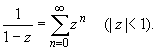
Date: 2015-07-02; view: 630; Нарушение авторских прав