Логарифмическая функция

Логарифмическая функция Ln z, при z 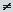0 определяется как обратная к показательной функции, причем

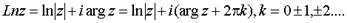
Так как показательная функция – периодическая с периодом 2p i, то логарифмическая функция является многозначной. В каждой точке z 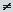0 она принимает бесконечно много значений.

Функция

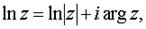
где arg z – главное значение аргумента, называется главным значением логарифмической функции. Итак,

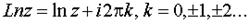
Известные правила о логарифме произведения и частного сохраняют свою силу и для многозначного логарифма, а именно: при z ₁ и z ₂, отличных от нуля, верны формулы

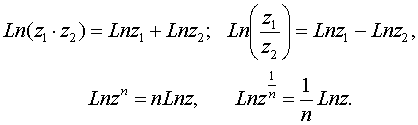
6. Общая степенная функция:

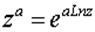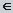, a C.

Эта функция многозначная, её главное значение равно .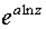

При a =1/ n, n 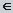N получаем многозначную функцию – корень n -й степени из z:

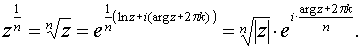
Условия Коши — Римана, называемые также условиями Даламбера — Эйлера — соотношения, связывающие вещественную 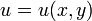и мнимую 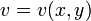части всякой дифференцируемой функции комплексного переменного 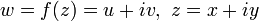. В декартовых координатах

Для того чтобы функция 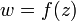, определённая в некоторой области 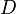комплексной плоскости, была дифференцируема в точке 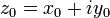как функция комплексного переменного 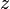, необходимо и достаточно, чтобы её вещественная и мнимая част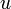и и 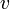были дифференцируемы в точке 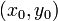как функции вещественных переменных и 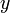и чтобы, кроме того, в этой точке выполнялись условия Коши — Римана:

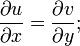
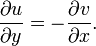
Компактная запись:

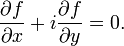
Если условия Коши — Римана выполнены, то производная 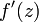представима в любой из следующих форм:

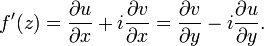
[править]Доказательство

[править] 1. Необходимость

По условию теоремы существует предел

,

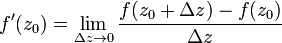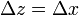не зависящий от способа стремления к нулю. Положим и рассмотрим выражение

.

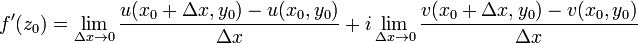Из существования предела комплексного выражения следует существование действительной и мнимой его частей. Поэтому в точке 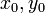существуют частные производные по x функций u(x,y) и v(x,y) и имеет место формула

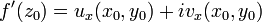
Полагая 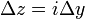, находим

.

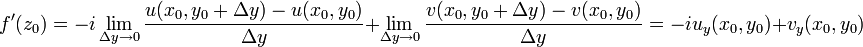Сравнивая две последние формулы, убеждаемся в справедливости условий Коши-Римана.

[править] 2. Достаточность

По определению дифференцируемости, приращения функци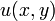й и 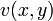в окрестности точки 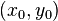могут быть записаны в виде

,

,

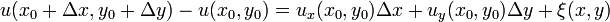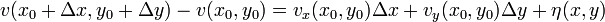где функци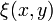и и 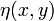стремятся к нулю при 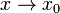, 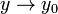быстрее, чем 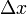и 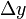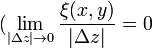, , 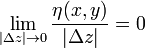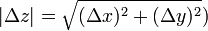. Составим теперь разностное соотношени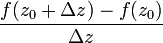е , где 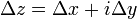и преобразуем его к виду

.

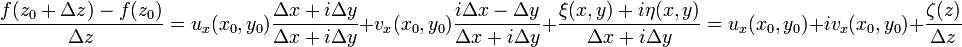
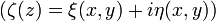Заметим, что при стремлении 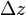к нулю последнее слагаемое этой формулы стремится к нулю, а первые остаются неизменными. Поэтому существует предел 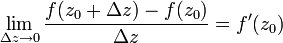, что и доказывает дифференцируемость функции 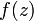в точке .

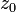Date: 2015-07-02; view: 420; Нарушение авторских прав