Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Нахождение тригонометрических функций острого и тупого углов с помощью тригонометрического круга
|
|
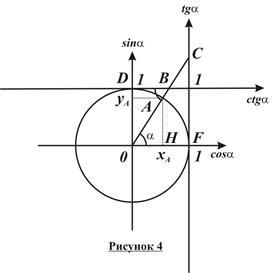Построим окружность единичного радиуса и отложим острый угол α в направлении против часовой стрелки от положительного направления оси абсцисс (рисунок 4). Пусть A – точка пересечения стороны построенного угла с окружностью, а H – ее проекция на ось абсцисс. Тогда из прямоугольного треугольника OAH получаем, что
; 
.
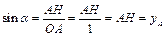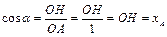Из полученных выражений видно, что с помощью единичной окружности удобно находить синус и косинус острого угла. Для этого надо отложить от положительного направления оси абсцисс заданный угол и найти точку пересечения его стороны с окружностью. Тогда абсцисса этой точки будет равна косинусу, а ордината – синусу построенного угла.
В связи с этим единичную окружность, используемую для нахождения тригонометрических функций углов, называют тригонометрическим кругом, а оси абсцисс и ординат – соответственно осями косинусов и синусов.
Для нахождения с помощью тригонометрического круга тангенса и котангенса острого угла удобно использовать специальные оси: вертикальную ось тангенсов, проходящую через точку (1;0), и горизонтальную ось котангенсов, проходящую через точку (0;1). По рисунку 4 видно, что если C – точка пересечения стороны угла α с осью тангенсов, то из прямоугольного треугольника OCF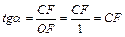 
, то есть тангенс острого угла α равен координате точки C, отсчитываемой вдоль оси тангенсов. Аналогично, если B – точка пересечения стороны угла с осью котангенсов, то котангенс угла α равен координате точки B, отсчитываемой вдоль оси котангенсов: из прямоугольного треугольника ODB 
.
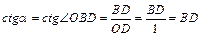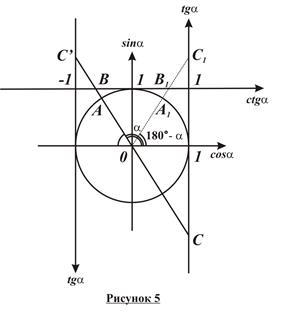Договоримся определять тригонометрические функции тупого угла аналогичным образом: для нахождения тригонометрической функции тупого угла α отложим его от положительного направления оси косинусов в направлении против часовой стрелки и найдем точки пересечения его стороны или ее продолжения с тригонометрическим кругом и осями тангенсов и котангенсов (рисунок 5). Тогда так же, как и для острого угла,
; 
;
; 
.
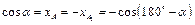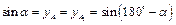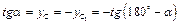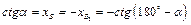Полученные соотношения показывают, что синусы смежных углов равны, а косинусы, тангенсы и котангенсы противоположны.
Замечание 1: Чтобы для нахождения тангенса тупого угла не приходилось продолжать его сторону, удобно использовать вторую ось тангенсов, изображенную на рисунке 5. Тогда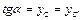 
.
Замечание 2: В соответствии с определениями синуса и косинуса острого и тупого углов,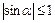 
и 
.
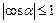Замечание 3: Пользуясь тригонометрическим кругом, можно найти тригонометрические функции углов в 0°, 90° и 180°:
| sin | cos | tg | ctg | |
| 0° | неопределен | |||
| 90° | неопределен | |||
| 180° | -1 | неопределен |
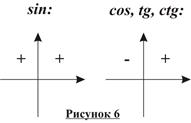
Замечание 4: На рисунке 6 показаны знаки тригонометрических функций острых и тупых углов.
Пользуясь тригонометрическим кругом, легко проследить за поведением тригонометрических функций при изменении угла от 0 до 180°:
· При увеличении угла от 0 до 180° его косинус уменьшается от 1 до -1.
· При увеличении угла от 0 до 90° его синус возрастает от 0 до 1, а при дальнейшем увеличении угла от 90° до 180° его синус убывает от 1 до 0.
· При увеличении угла от 0 до 90° его тангенс возрастает от 0 до ∞, а при дальнейшем увеличении угла от 90° до 180° его тангенс возрастает от -∞ до 0.
· При увеличении угла от 0 до 180° его котангенс убывает от ∞ до -∞.
Date: 2015-07-01; view: 1025; Нарушение авторских прав