
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Методы решения ТЗ
|
|
Транспортная задача является одной из основных оптимизационных математических задач. Впервые постановка ТЗ была проведена в 1930г. в трудах советского экономиста А. Толстого. В 1941г. решение ТЗ предложил венгерский экономист Эгервари, поэтому один из методов решения ТЗ называется «венгерский метод». В 1941г. решение задачи окончательно сформулировал американский математик Хичхок.
В СССР внедрение математических методов решения задач было осуществлено в 1958г. в автотранспортной промышленности.
В дальнейшем обнаружилось, что алгоритм ТЗ можно применять для решения широкого круга, которые иногда не имеют ничего общего с транспортировкой грузов, но название «транспортная» осталось исторически. при этом величина «стоимость перевозки» может означать расстояние, стоимость изделия, время, производительность и т.д.
a) Получение математической модели классической транспортной
задачи.
Дано: на трех станциях отправления А1, А2, А3 сосредоточено соответственно а1, а2 и а3 тонн грузов. Эти грузы надо доставить в 4 пункта назначения В1,В2,В3 и В4 соответственно b1, b2, b3,b4. При этом сумма запасов на Аi (i=1,2,3) равна сумме потребностей на Bj(j=1,2,3,4),или
а1+ а2+ а3= b1+b2+ b3 +b4, или в общем виде:
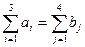
Транспортные расходы на перевозку 1т груза от станции i в пункт j известны и обозначаются Сij
Требуется составить такой план перевозок, чтобы:
- общие расходы по перевозке были минимальными;
- был полностью удовлетворен спрос на Bj
- был полностью вывезен груз с Аi
Решение.
Обозначим х11 – кол-во груза перевозимого из А1 в В1
х12 – кол-во груза перевозимого из А1 в В2
и т.д., в общем виде хij – кол-во груза, перевезенного из станции i в пункт назначения j.
Полученные исходные данные удобнее записать в виде специальной таблицы:
| пункт назначения | В1 | В2 | В3 | В4 | запасы |
| ст. отправления | |||||
| А1 | x11 | x12 | x13 | x14 | a1 |
| c11 | c12 | c13 | c14 | ||
| А2 | x21 | x22 | x23 | x24 | a2 |
| c21 | c22 | c23 | c24 | ||
| А3 | x31 | x32 | x33 | x34 | a3 |
| c31 | c32 | c33 | c34 | ||
| потребности | b1 | b2 | b3 | b4 |
С одной стороны:
общее кол-во груза, доставленного в В1 равно
b1= x11+x21+x31 , т.е. потребность в грузе удовлетворена.
С другой стороны:
общее количество груза отправленного с А1 равно
a1=x11+x12+x13+x14, т.е. груз вывезен полностью.
Аналогично рассуждая запишем остальные равенства:
b2= x12+x22+x32 a2=x21+x22+x23+x24
b3= x13+x23+x33 и a3=x31+x32+x33+x34
b4= x14+x24+x34
Тогда общие транспортные расходы составят:
Z=c11x11+c21x21+c31x31+c12x12+c22x22+c32x32+c13x13+c23x23+c33x33+c14x14+c24x24+
+c34 x34,
или в общем виде: 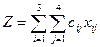
Таким образом, математическая модель ТЗ имеет вид:
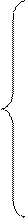 среди неотрицательных решений системы:
среди неотрицательных решений системы:
a1=x11+x12+x13+x14
a2=x21+x22+x23+x24
a3=x31+x32+x33+x34
b1= x11+x21+x31
b2= x12+x22+x32
b3= x13+x23+x33
b4= x14+x24+x34
выбрать такое, при котором 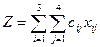 было бы минимальным.
было бы минимальным.
Или для общего случая:
при условии, что
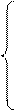
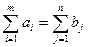 (сумма запасов на всех станциях отправления равна сумме потребностей пунктов назначения)
(сумма запасов на всех станциях отправления равна сумме потребностей пунктов назначения)
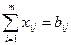
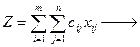 min
min
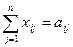
б) Методы решения транспортной задачи.
В общем случае решение ТЗ сводится к построению по определенным правилам базисного или опорного плана перевозок, который затем оптимизируется с целью получения минимальных транспортных затрат.
Наиболее известными методами построения опорных планов являются:
- метод северо-западного угла;
- метод минимального элемента;
- аппроксимация Фогеля;
- метод двойного предпочтения.
Полученный таким образом опорный план оптимизируется одним из следующих методом:
- метод потенциалов;
- метод дифференциальных рент;
- венгерский метод;
- дельта-метод;
- распределительный метод.
На практике наиболее часто используется метод потенциалов. Впервые был предложен в 1949г. советскими математиками Канторовичем и Гавуриным, окончательно был сформирован американцем Данцигом. Суть плана – текущий базисный план проверяется на оптимальность, при необходимости осуществляется переход к «лучшему» базисному плану.
Литература: 2, 5-25 с.
Контрольные вопросы:
1. Почему транспортная задача называется транспортной?
2. В чем ее суть?
3. Какие методы ее решения Вы узнали?
Date: 2015-07-01; view: 1132; Нарушение авторских прав