Молекулярно–кінетична інтерпретація явищ переносу

Розглянемо модель ідеального газу, у якій молекули через хаотичність теплового руху рухаються по трьох напрямках X, Y і Z так що на кожен напрямок в одну сторону рухається 1/6 від загальної кількості молекул:

,

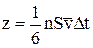і густина потоку молекул складає:

.

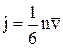Ці потоки і є переносниками визначених фізичних величин G. Густину потоку величини G позначимо 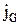. Будемо вважати, що через цікавлячу нас площадку S молекули будуть переносити те значення величини G, що вони мали на відстані l від площадки S, де l – довжина вільного пробігу молекули, тобто відстань, яку пролітає частинка між двома послідовними зіткненнями. Середню швидкість руху молекули можна представити таким чином:

.

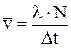Якщо за секунду молекула здійснює 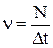зіткнень, то формулу швидкості можна переписати: 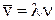і середня довжина вільного пробігу буде дорівнювати:

.

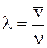При своєму русі молекула здійснює стільки зіткнень, скільки зустрінеться на її шляху молекул, центри яких знаходяться в межах обсягу циліндра радіуса d (де d – діаметр молекули). Якщо концентрація молекул n, то можна записати:

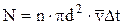і .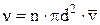

Після підстановки одержуємо:

.

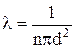Розрахунок показує, що врахування відносної швидкості руху молекул зменшує середню довжину вільного пробігу молекул у 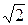разів, тобто

.

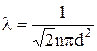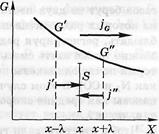Нехай величина G характеризує визначену молекулярну властивість, що віднесена до однієї молекули. Це може бути енергія, імпульс, електричний заряд та ін. При наявності градієнта величини G повинний виникнути потік убік її зменшення. Нехай величина G міняється тільки в напрямку осі X. Площадку S будуть пронизувати молекули, що рухаються в зустрічних напрямках, їхні густини потоків дорівнюють 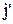и 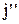, причому вони повинні дорівнювати один одному, щоб не виникало газодинамічних потоків. Тоді для результуючої густини потоку величини G можна записати:

.

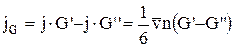Завдяки різниці l різницю значень 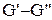представимо у вигляді:

.

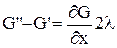З урахуванням останньої формули можна записати:

.

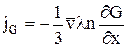Отримане рівняння є загальним рівнянням явища переносу. Розглянемо застосування цього рівняння до розглянутих раніше процесів.

Дифузія. Якщо G – характеристика перенесеної речовини, віднесеної до однієї молекули, то 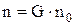, відкіля випливає, що 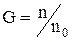, де n₀ – рівноважна концентрація. Тоді рівняння переносу буде мати вигляд:

.

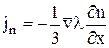Зіставивши отримане рівняння з емпірично отриманим, одержуємо, що коефіцієнт дифузії дорівнює:

.

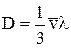В'язкість (внутрішнє тертя). G – імпульс молекули, перенесений через площадку S: 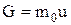. Після підстановки одержуємо:

,

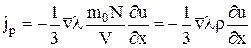де 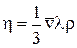– коефіцієнт в'язкості.

Теплопровідність. G – середня енергія теплового руху, що приходиться на одну молекулу:

.

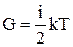Після підстановки одержуємо:

.

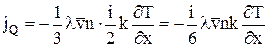Спростимо отриману формулу, використовуючи поняття питомої теплоємності с_v. Оскільки 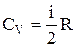і 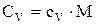, то одержуємо:

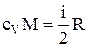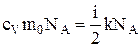, і .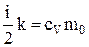

Помножимо обидві частини останньої формули на концентрацію молекул:

.

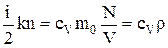Після відповідної заміни формула переносу тепла здобуває вигляд:

,

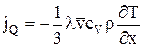де 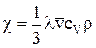– коефіцієнт теплопровідності.

Аналіз коефіцієнтів переносу дозволяє зробити наступні висновки:

1. визначивши за емпіричними формулами коефіцієнти переносу, можна обчислити середню довжину вільного пробігу l і діаметр d молекул;

2. усі три коефіцієнти з ростом температури Т збільшуються, оскільки ~ ;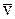

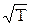3. Оскільки l~1/n, а n~r, то як в'язкість h, так і теплопровідність c не залежать від концентрації, а значить і від тиску (при незмінній температурі).

Date: 2015-07-01; view: 566; Нарушение авторских прав