Задача розподілу ресурсів між підприємствами

Типова задача динамічного програмування (ДП) – розподілити ресурси між підприємствами на початку кожного року таким чином, щоб сумарний прибуток від усієї системи підприємств за певний період (Т) був максимальний.

Крок управління – перерозподіл ресурсів на початку кожного року.

Крокове управління на і-му кроці – сукупність виділених ресурсів підприємствам на і-му році.

Стратегія управління – сукупність крокових управлінь; її ефективність оцінюється показником ефективності (наприклад, отриманим прибутком).

Розподілити ресурси оптимально в кожному році неможливо без урахування майбутніх наслідків, тому процес динамічного програмування розгортається від кінця до початку, – таким чином знаходимо умовне оптимальне управління), а потім – від початку до кінця; серед умовних знаходяться вже оптимальні управління з урахуванням результатів попереднього кроку (початкові умови наступного року).

Розглянемо дану задачу дещо в спрощеному вигляді: як систему управління (розподілу) ресурсами між двома підприємствами з використанням лінійної регресійної моделі і умови “або все – або нічого”.

Задача розподілу ресурсів. Маємо два автотранспортні підприємства, що входять до деякого автотранспортного об’єднання. Розглянемо задачу розподілу ресурсів (капіталовкладення К) між цими підприємствами на період Т = 5 років з наступними коефіцієнтами, що є коефіцієнтами лінійних регресій, які в свою чергу є моделями функцій залишку ресурсів і отриманого року діяльності підприємств:

a – коефіцієнт щорічного прибутку І-го АТП;

b – коефіцієнт щорічного прибутку ІІ-го АТП;

g – коефіцієнт амортизації використання фондів І-го АТП;

q – коефіцієнт амортизації використання фондів ІІ-го АТП;

х – сума основних фондів, що розподіляється в І-е АТП;

у – сума основних фондів, що розподіляється в ІІ-е АТП;

К = х + у – капіталовкладення на весь період Т;

j(х_і) = gх_і – закон зменшення початкової суми вкладених ресурсів в І-е АТП;

j(y_і) = qу_і – закон зменшення початкової суми вкладених ресурсів в ІІ-е АТП;

f_і = j(х_і) + j(y_і) – залишки від вкладань після кожного року поточного періоду, що не йдуть в прибуток (z_i), а перерозподіляються підприємствам на наступний рік (f_і = к_і+1), де х_і + y_і = к_і (і=1,...,5) – сума капіталовкладень в обидва підприємства на кожному році періоду, що розглядається.

Оскільки х_і + y_і = к_і , то y_і = к_і – х_і – обсяг ресурсів, вкладених в ІІ-е підприємств; тоді

f_і = gх_і + qу_і = gх_і + q (к_і – х_і) = (g – q)х_і + q к_і ,

тобто залишок розраховується за формулою:

f_і = (g– q)х_і + q к_і (27)

Відповідно розпишемо розрахункову формулу одержаних прибутків:

z_i = aх_і + bу_і = aх_і + b(к_і – х_і) = (a– b)х_і + bк_і,

тобто:

z_i = (a– b)х_і + bк_і (28)

Розподілити ресурси між підприємствами таким чином, щоб отриманий прибуток був максимальний. Розглянемо три задачі з різними умовами: прибутки після кожного року діяльності підприємств відраховуються в автотранспортне об’єднання; прибутки вкладаються кожного року в подальший розвиток підприємств; змішаний тип задачі.

1. Задача розподілу ресурсів за умови відрахування отриманих прибутків в автотранспортне об’єднання після кожного року діяльності.

Задамо вхідні дані, які або розраховуються або задаються на основі статистичних даних відповідними службами головного підприємства:

a = 0,6, b = 0,7, g = 0,8, q = 0,85, Т= 5. Якщо параметри a, b, g, q в кожному році будуть різними, то задачі такого типу називаються задачами з неоднорідними етапами.

Сума прибутку, що отримується кожного року, надходить в автотранспортне об’єднання; залишок після останнього року даного періоду до прибутку не додається. Шукаємо умовне оптимальне управління, починаючи з 5-го року.

Функціональна модель задачі:

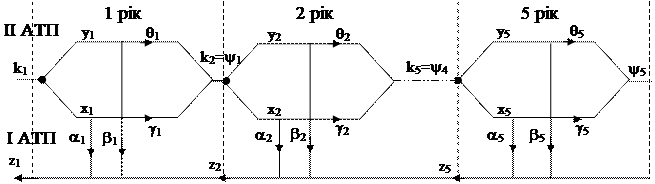Етап 5.

Підраховуємо залишок після 5-ти років діяльності обох підприємств, що не йде в прибуток, і величину прибутку:

f₅ = (g – q)х₅ + q к₅ = (0,8 – 0,85)х₅ + 0,85к₅ = – 0,05 х₅ + 0,85 к₅

z₅ = (a– b)х₅ + bк₅ = (0,6 – 0,7) х₅ + 0,7к₅ =– 0,1 х₅ + 0,7 к₅

Знаходимо максимальний прибуток за принципом: одному підприємству віддати всі ресурси, іншому – нічого:

z_5(max) = 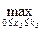(–0,1 х₅ + 0,7 к₅) = 0,7 к₅

Максимум досягається, якщо к₅ = 0, тобто на 5-му році ІІ-му підприємству віддали всі ресурси: у₅ = к₅.

Етап 4.

Аналогічні розрахунки проводимо на кожному етапі.

f₄ = (0,8 – 0,85)х₄ + 0,85к₄ = -0,05 х₄ + 0,85 к₄ º к₅

Date: 2015-07-01; view: 436; Нарушение авторских прав