
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Побудова регресійних моделей
|
|
Це стосується побудови лінійної регресійної моделі з одним аргументом, тобто y(x1), в першій задачі, нелінійної регресії – в другій та лінійної регресійної моделі y(x1,x2) - в третій задачі. Розглянемо методику отримання цих моделей.
Математична лінійна регресійна модель y(x) має вигляд:
y(x) = bo + b1·x, (1)
де bo - вільний член, b1 - коефіцієнт впливу x на y. В завданні, що пропонується студенту, необхідно чисельно визначити значення bo та b1.
На площині yx наносяться точки i (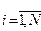 ), де N - число виборок, які відповідають значенням yi та xi. На отриманому полі, що називається кореляційним, проводиться пряма лінія y(x) таким чином, щоб відхилення yi від цієї лінії відповідали умові:
), де N - число виборок, які відповідають значенням yi та xi. На отриманому полі, що називається кореляційним, проводиться пряма лінія y(x) таким чином, щоб відхилення yi від цієї лінії відповідали умові:
U = 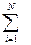 [yi - y(xi)]2 = min, (2)
[yi - y(xi)]2 = min, (2)
де y(xi) - значення y (теоретичні), отримані з допомогою (1) при підстановці в цю формулу x = xi.
Особливо відмітимо, що пряма y(x) зовсім необов'язково повинна проходити через будь-яку експериментальну точку yi, але сума квадратів відхилень yi від y(xi) при цьому має бути мінімальною. Якщо вираз у формулі (2) поділити на N, то ми отримаємо більш зрозумілу умову:
U' = 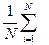 [yi - y(xi)]2 = min (3)
[yi - y(xi)]2 = min (3)
у вигляді вимоги забезпечення мінімуму дисперсії відхилень yi відносно лінійної математичної регресійної моделі y(x). Тому цей метод пошуку оптимального розташування y(x) на регресійному полі має назву "метод мінімізації середнього квадрату" або "метод мінімізації дисперсії відхилень".
Щоб забезпечити умову (2), необхідно взяти похідну від U по параметрам a та b, прирівняти її нулю; тоді отримані значення a та b відповідатимуть умові (2) або (3).
Отже:
U = 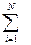 [yi - (bo + b1·x)]2;
[yi - (bo + b1·x)]2;
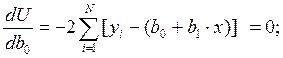
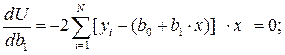
звідси отримаємо наступні рівняння, що підлягають нормальному розв'язку:
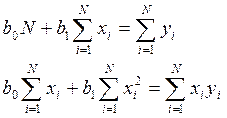 (4)
(4)
Розв'язок цієї системи відносно bо та b1 здійснюється за допомогою правил Крамера чи Дулітла, в результаті чого отримаємо наступні формули:
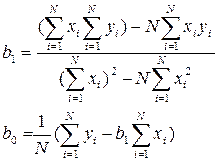 (5)
(5)
Якщо помножити вираз у формулі (5) для b1 на (-1) та поділити чисельник і знаменник на N, то можна отримати іншу форму запису цієї формули, більш зручну для користування.
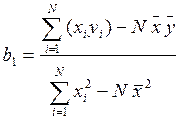
(6)
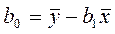
Після закінчення розрахунків bо та b1 проводиться перевірка гіпотези про лінійність зв'язку між y та x за допомогою коефіцієнта лінійної кореляції R (як оцінити отриману модель на адекватність статистичним даним покажемо на прикладі двофакторної лінійної регресії):
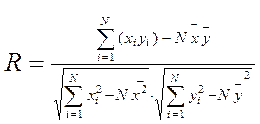 (7)
(7)
Чим ближче значення /R/ до одиниці, тим вірогідніша лінійність y(x). При цьому знак R визначається знаком коефіцієнта b1 (якщо b1>0, то і R > 0 і навпаки). Вважається, що лінійна модель якнайкраще описує досліджуваний процес, якщо /R/≥ 0,7.
Зведення нелінійної регресії до лінійної. Наприклад, вигляд розташування точок на кореляційному полі нагадує форму деяких нелінійних функцій:
а) гіперболічна функція 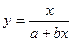
Необхідні перетворення: 
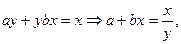 вводимо заміну
вводимо заміну 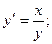
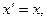
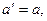
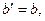 і отримуємо лінійну форму гіперболічної функції
і отримуємо лінійну форму гіперболічної функції 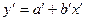 ;
;
б) експоненційна функція 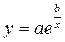
Аналогічно: 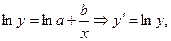
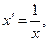
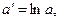
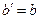 .
.
Подібні перетворення інших функцій зводяться в таблицю, наведену у завданні для самостійних робіт на побудову нелінійних регресій. Отримавши лінійну форму і застосувавши до неї метод найменших квадратів і табличний перехід до нелінійних параметрів регресії, матимемо нелінійну регресію.
Математична модель, що є лінійною моделлю з двома змінними (факторами) y(x1;x2), має вигляд:
y = bo + b1·x1 + b2·x2. (8)
Зробивши висновки, аналогічні для моделі y(x), можна отримати систему рівнянь відносно невідомих коефіцієнтів bo, b1, b2 у вигляді:
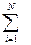 (x'1i)2 b1 +
(x'1i)2 b1 + 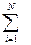 (x'1ix'2i)b2 =
(x'1ix'2i)b2 = 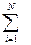 (x'1iy'i)
(x'1iy'i)
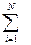 (x'2ix'1i)b1 +
(x'2ix'1i)b1 + 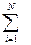 (x'2i)2 b2 =
(x'2i)2 b2 = 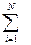 (x'2iy'i) (9)
(x'2iy'i) (9)
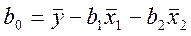
де:
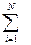 x'1iy'i =
x'1iy'i = 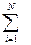 (x1iyi) – N
(x1iyi) – N 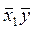 (10)
(10)
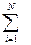 (x'1i)2 =
(x'1i)2 = 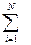 (x1i)2 – N(
(x1i)2 – N(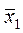 )2 (11)
)2 (11)
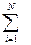 x'2iy'i =
x'2iy'i = 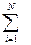 (x2iyi) – N
(x2iyi) – N 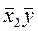 (12)
(12)
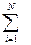 x'1ix'2i =
x'1ix'2i = 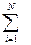 (x1ix2i) –N
(x1ix2i) –N 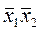 (13)
(13)
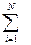 (x'2i)2 =
(x'2i)2 = 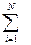 (x2i)2 – N (
(x2i)2 – N (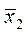 )2 (14)
)2 (14)
Після того, як величини, що входять в формули (10) - (14) розраховані, розв'язується система рівнянь (9) відносно bo, b1, b2 за допомогою правила Крамера.
Коефіцієнт b1 в моделі y = bo + b1x1 носить назву "повний коефіцієнт регресії", який відображає вплив x1 на y без урахування впливу x2 на y (цей вплив враховується певним чином в значенні b1).
Напроти, коефіцієнт b1 в моделі y = bo + b1·x1 + b2·x2 носить назву "частинний коефіцієнт регресії" (іноді - "чистий коефіцієнт регресії"), який відображає тільки вплив x1 на y, виключаючи повністю вплив x2 на y. Те ж саме стосується коефіцієнта b2. Тому потрібно пам'ятати, що врахування найбільшої (в розумних межах) кількості змінних поліпшує точність оцінки впливу кожної з розглянутих змінних.
Аналіз отриманих моделей.
Для оцінки моделей з багатьма змінними, а також з однією змінною, застосовуються наступні показники варіації:
1) Загальна дисперсія:
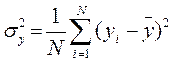 (15)
(15)
2) Факторна дисперсія, що відображує вплив тільки тих змінних, які розглядаються:
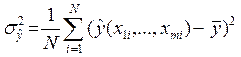 (16)
(16)
3) Залишкова дисперсія (дисперсія помилок моделі):
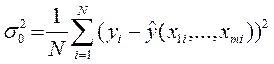 (17)
(17)
або в більш спрощеному вигляді
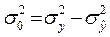 (18)
(18)
Відношення
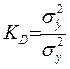 (19)
(19)
називається коефіцієнтом детермінації (у випадку лінійної множинної регресії) або індексом детермінації (у випадку нелінійної множинної регресії). Фізично він характеризує частку впливу вибраних змінних хj в загальній варіації у.
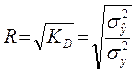 (20)
(20)
де R – коефіцієнт множинної кореляції (або індекс кореляції для нелінійної регресії). Значення цього коефіцієнта, розрахованого за даною формулою (21), співпадає зі значенням R, розрахованим за формулою (9) для лінійної парної регресії. З урахуванням того, що  , маємо ще одну розрахункову формулу:
, маємо ще одну розрахункову формулу:
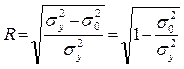 (21)
(21)
тобто коефіцієнт кореляції розраховується по дисперсії  помилок моделі
помилок моделі 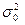 і по загальній дисперсії
і по загальній дисперсії 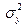 . Розглянемо даний матеріал на конкретному прикладі.
. Розглянемо даний матеріал на конкретному прикладі.
Приклад. Визначити регресійну модель впливу капіталовкладень в розвиток виробництва (х1), розміру основного капіталу (х2) ті чисельності працюючих (х3) на прибуток, який отримає підприємство після року своєї діяльності, (у). Експериментальні дані отримані в результаті огляду семи аналогічних підприємств і занесені в таблицю (N=7).
| У(тис.у.о.) | |||||||
| Х1(тис.у.о.) | |||||||
| Х2(тис.у.о.) | |||||||
| Х3(тис.у.о.) |
Проведемо послідовний аналіз впливу:
1) капіталовкладень х1 на прибуток у (перша модель); 2) капіталовкладень х1 і основних фондів х2 на прибуток у (друга модель); 3) всіх трьох змінних х1, х2 і х3 на у (третя модель); і прослідкуємо як при цьому змінюються параметри моделі (чисті коефіцієнти регресії) і показники точності отриманих моделей. Розрахунок виконаний ПЕОМ із застосуванням програми “MATНCAD-2”. Приведемо деякі розраховані дані:
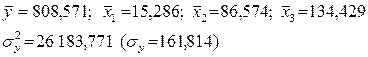

Для І моделі: 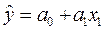 маємо:
маємо:
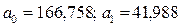 тоді
тоді
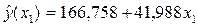
Для розрахунків дисперсій визначимо за отриманою моделлю значення 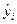 і для порівняння з експериментальними даними занесемо їх в таблицю:
і для порівняння з експериментальними даними занесемо їх в таблицю:
| уі | |||||||
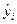
| 586,63 | 796,57 | 838,563 | 628,62 | 736,575 | 964,526 |
Застосовуючи формули (16), (17), (19) і (20), визначимо:
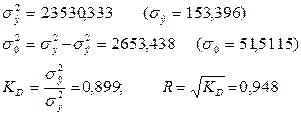
В дужках розраховані значення середньо квадратичних відхилень:
Для ІІ моделі: 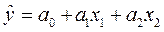 маємо:
маємо:
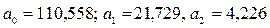 ; тоді
; тоді
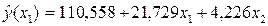
Представимо аналогічну таблицю:
| уі | |||||||
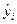
| 589,874 | 753,461 | 825,904 | 645,904 | 821,079 | 950,258 |
і відповідні оцінки дисперсій та середньо квадратичних відхилень:
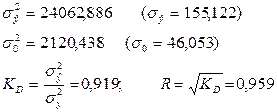
Оскільки s 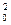 (ІІ) < s
(ІІ) < s 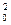 (І), а R(ІІ) > R(І), то можна зробити висновок, що ІІ модель більш точно описує модель в загальному вигляді.
(І), а R(ІІ) > R(І), то можна зробити висновок, що ІІ модель більш точно описує модель в загальному вигляді.
Для ІІІ моделі: 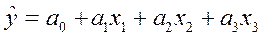 маємо:
маємо:
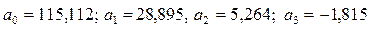 ; тоді
; тоді
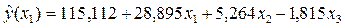
Таблиця матиме вигляд:
| уі | |||||||
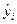
| 588,965 | 761,953 | 824,986 | 649,087 | 813,515 | 936,371 |
Відповідні значення:
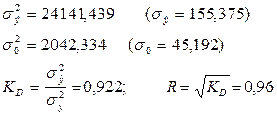
Оскільки s 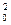 (ІІІ) < s
(ІІІ) < s 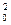 (ІІ), а R(ІІІ) > R(ІІ), значить дана модель більш точно описує взаємозв’язки в даному об’єкті. Те, що а3 < 0, означає неефективне використання чисельності працівників, або безпідставно збільшена заробітна плата (в межах тих даних, на яких базується даний аналіз).
(ІІ), а R(ІІІ) > R(ІІ), значить дана модель більш точно описує взаємозв’язки в даному об’єкті. Те, що а3 < 0, означає неефективне використання чисельності працівників, або безпідставно збільшена заробітна плата (в межах тих даних, на яких базується даний аналіз).
Date: 2015-07-01; view: 1355; Нарушение авторских прав