Загальна теорія систем

Будь-яка система управління (як технічна, так і організаційна) базується на двох основних принципах управління:

- управління по збуренню;

- управління по відхиленню.

Можлива побудова системи з використанням обох принципів одночасно, - така система є комбінованою. Кожен об'єкт управління має: змінну, якою управляють (φ); змінну, яка управляє (μ); збурення (λ).

Система управління по збуренню. Структурна схема системи, що реалізує принцип управління по збуренню має наступний вигляд:

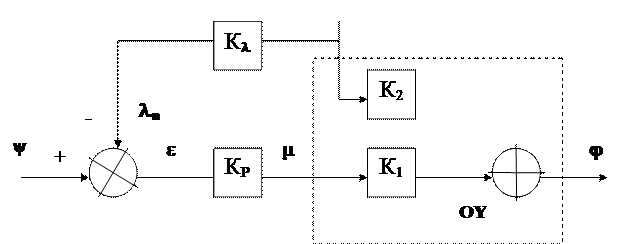Рис.1. Структурна схема системи управління по збуренню λ.

На рис.1 зображено: OY – об'єкт управління, що має вихідну змінну φ (наприклад, власний обсяг продажу), та дві вхідні змінні: μ – змінна, яка управляє (наприклад, ціна продажу), і λ – збурення, що впливє на φ, але не залежить від μ (наприклад, обсяг продажу конкурентів); К_р – регулятор (наприклад, регулятор ціноутворення), який змінює μ залежно від відхилення (ε) між завданням на продаж ψ та інформацією (λ_n) про збурення λ, що має місце на поточний час; компаратор ε = (ψ – λ_n), який порівнює ψ з λ_n та впливає на рішення про змінення змінної, яка керує (μ).

Коефіцієнти, що знаходяться в квадратах-блоках системи, означають відповідно:

К_λ – коефіцієнт впливу λ на λ_n, тобто λ_n = К_λ λ (якщо інформація про λ

надходить без перекручень, то К_λ = 1);

К_р – коефіцієнт впливу ε на μ, тобто μ= К_р ε = К_р(ψ – λ_n);

К₁ та К₂ – відповідно коефіцієнти впливу μ та λ на φ, тобто φ= К₁μ + К₂λ. По суті, φ = К₁μ+ К₂λ представляє собою лінійну математичну модель системи (наприклад, системи збуту автомобілів, якщо вважати К₁ = – а та К₂= – b).

Враховуючи сказане вище, можна визначити залежність φ від ψ та λ таким чином:

φ= К₁μ+ К₂λ = К₁К_р(ψ – λ_n) + К₂λ = К₁К_р(ψ – К_λ·λ) + К₂λ =

= К₁К_рψ – К₁К_рК_λ·λ + К₂λ

Накінець матимемо:

ψ= К₁К_рψ – (К₁К_рК_λ – К₂)λ (22)

Щоб забезпечити незалежність φ від λ, необхідне виконання умови К₁К_рК_λ – К₂ = 0, тобто К_рК_λ = К₂ / К₁. Якщо прийняти К_λ = 1 (інформація надходить без перекручень), то матимемо:

К_р =К₁ / К2, (2) (23)

тобто необхідну величину коефіцієнта К_р, що забезпечить незалежність φ від λ.

Таким чином, маючи модель системи збуту автомобілів, як вказано в одному з варіантів завдання, можна визначити необхідне значення коефіцієнта ціноутворення К_р, який забезпечує незалежність власного обсягу продажу від обсягу продажу конкурентів шляхом відповідної зміни вартості продажу. Студенту залишається тільки правильно визначити, чи відповідає його варіант завдання розглянутому типу системи.

Система управління по відхиленню. На відміну від попереднього типу систем управління, системи цього типу мають безпосередній зв'язок змінної, якою управляють (φ), з компаратором системи (так званий зворотній зв'язок виходу зі входом). Структурна схема систем цього типу представлена на рис.2.

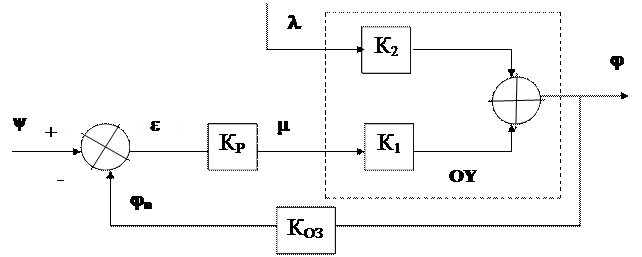
Рис.2. Структурна схема системи управління по відхиленню ε.

Позначення елементів системи прийняти ті ж, що і в попередній системі. Згідно з рис.2 зміна значення змінної μ, яка керує значенням φ, здійснюється з урахуванням відхилення ε= ψ – φ_n. Завдяки зв'язку між φ_n та φ, через коефіцієнт впливу К_оз, система діє таким чином, щоб величина відхилення ε була мінімальною навіть тоді, коли має місце значне збурення λ. Відмітимо, що в першому завданні цієї самостійної роботи є як системи управління по збуренню, так і системи управління по відхиленню. Якщо запропонована система збуту автомобілів відноситься до систем цього типу (тобто керує ціною збуту згідно з коливаннями обсягу власного продажу), то в такому випадку розв'язок даної задачі необхідно проводити за допомогою формул, що приводяться нижче.

Математична модель об'єкту залишається в тому ж вигляді: φ = К₁μ + К₂λ, але з урахуванням ε= ψ – φ_n; φ_n = К_оз·φ; μ= К_р·ε, будемо мати:

φ = 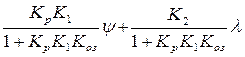(24)

що визначає залежність коливань φ від коливань завдання ψ та коливань збурення λ (для задачі, що пропонується в завданні, це залежність коливань обсягу продажу (V_n) від коливань завдання на продаж (ψ) та коливань обсягу продажу конкурентів (V_к). Всі ці змінні вимірюються у відсотках відхилення від сталого значення.

За допомогою формули (24) можна розрахувати коливання V_n (у відсотках) при заданих розмірах коливань V_k (у відсотках) та заданому значенні коефіцієнта регулятора ціноутворення при незмінності завдання (коли ψ = 0).

Неважко продемонструвати, що коливання ціни продажу (μ) визначається за формулою:

μ = 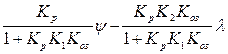(25)

При ψ = 0 можна визначити μ при заданих λ та К_р. У випадку, коли необхідно визначити коливання відхилення ε (у нашому випадку – це складські залишки непроданих автомобілів), розрахунки слід проводити за формулою:

ε = φ – φ_п = ψ - К_озφ = 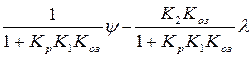(26)

Додамо наприкінці, що потрібно прийняти К_оз = 1, якщо інформація про обсяги власного продажу надходить у систему без перекручень.