Квадратурные формулы Гаусса

Во всех приведенных до сих пор формулах численного интегрирования Ньютона-Котеса и во всех формулах, получаемых методом Ромберга, используются равноотстоящие узлы. В случае квадратурных формул Гаусса это уже не так. Иначе говоря, смысл квадратурных формул Гаусса состоит в том, чтобы при наименьшем возможном числе узлов точно интегрировать многочлены наивысшей возможной степени. Можно показать, что при 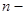гауссовых узлах по полученной формуле можно точно интегрировать многочлены степени .

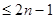(22)

Для количества узлов и соответствующих значений и 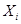- составлены таблицы, которые позволяют вычислять интегралы по формуле (22).

Для понимания сути этих таблиц рассмотрим пример.

Пример:

Пусть нам нужно составить квадратурную формулу с двумя узлами 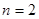,по которой точно интегрируются многочлены до 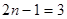степень включительно.

Решение: Искомая формула имеет вид:

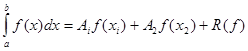, (23)

где 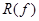- остаток, который обращается в нуль, для

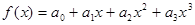, при .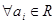

Тогда, подставляя в (23) имеем:

(24)

Отсюда, приравнивая коэффициенты при 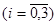, справа и слева, получаем систему уравнений:

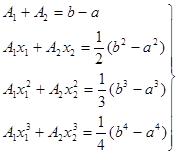(25)

Ее решение имеет вид:

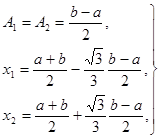(26)

Следовательно, искомая квадратурная формула такова:

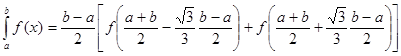. (27)

Ясно, что если нам нужно вычислить интеграл со многими узловыми точками, действуем следующим образом:

а) промежуток интегрирования 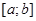делим на 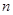- равных промежутков и на каждом маленьком промежутке 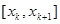применяем формулу Гаусса с неравноотстоящими узлами (27);

б) полученные результаты складываем.

В случае, когда 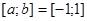, оказывается, что узловыми точками при делении отрезка на 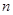- частей являются корни соответствующих многочленов Лежандра.

Для вычисления кратных интегралов, их сводят обычно к повторным интегралам, а далее применяют те же самые кубатурные формулы для каждого значения узловых точек, что и в одномерном случае. Однако, надо иметь в виду, что кратные интегралы значительно сложнее вычислять с заданной точностью.

Точность произведённых вычислений зависит от точности аппроксимации подынтегральной функции многочленами.

Date: 2015-06-11; view: 1213; Нарушение авторских прав