Достоверность разницы между средними арифметическими

Оценка достоверности разницы между средними арифметическими двух выборочных совокупностей (t) позволяет определить, случайна она, то есть в пределах ошибки выборочности или достоверна, то есть удовлетворяет требуемому уровню значимости.

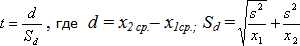
Эмпирическое значение сравнивается с табличными значениями t при разных уровнях значимости, на основании чего определяется достоверность различий.

При сравнении средних арифметических двух генеральных со­вокупностей любая разность между ними будет достоверна. В ве­теринарии, зоотехнии и т. д. приходится сравнивать между собой средние величины не генеральных совокупностей, а выборочных (породы, линии, семейства, опытная и контрольная группы и т. д.). Поэтому необходимо установить достоверность разности между средними двух групп. Недостаточно, например, знать, что 20 дочерей какого-то производителя превосходят по удою своих матерей. Следует, кроме того, вычислить критерий достоверности разности, чтобы с определенной вероятностью судить о том, что следующие 100, 200 и т. д. дочерей этого производителя также будут превосходить по молочности своих матерей в аналогичных условиях. Для оценки достоверности разности между средними арифметическими двух выборочных совокупностей применяется критерий достоверности (td), который вычисляют по формуле

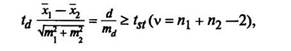
где mi, тг — ошибки сравниваемых выборочных средних арифметических х\, хг; d —разность между средними арифметическими х\, хг; пц — средняя ошибка выборочной разности; <«— стандартное значение критерия, определяемое по таб­лице Стьюдента (табл. 13) с учетом числа степеней свободы (v) для трех уровней вероятности; п\, пг — численность сравниваемых групп.

При проведении научных исследований в области биологии и экологии часто возникает необходимость дать оценку различий между статистическими параметрами, например, средними арифметическими, то есть определить, отличаются ли они друг от друга.
Например, сравниваются результаты контрольного и опытного вариантов, или данные, полученные разными методами. В этом случае сначала определяется разница между выборочными средними: d = M₁ - M₂ (из большей величины вычитается меньшая).
Затем находится ошибка репрезентативности разности (или просто ошибка):

, где

• m₁ – ошибка первой средней арифметической,
• m₂ – ошибка второй средней арифметической.

Зная ошибку разности m_d, можно найти генеральную разность:

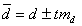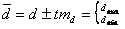или , где

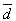• – генеральная разность,
• d – выборочная разность,
• t – критерий Стьюдента,
• m_d – ошибка репрезентативности разности.

В этом случае число степеней свободы ν = n₁ + n₂ - 2.
Достоверность разности определяется по формуле:

(вспомним, что при определении достоверности какого-либо показателя этот показатель делится на свою ошибку).
Здесь, как и в случае со средними арифметическими, возможны два варианта ответа:

1) если t ≥ t_st, то разница достоверна;
2) если t < t_st, то разница недостоверна.

23. Статистический анализ данных с помощью персонального компьютера

В условиях рыночной конкуренции процесс подготовки и принятия решений менеджерами компаний должен включать тщательный анализ имеющихся данных, базирующийся на методах математической статистики. В этой связи существенную помощь в получении необходимой информации могут оказать современные информационные технологии интеллектуального и статистического анализа данных. Оценка кредитных и страховых рисков, прогнозирование тенденций на финансовых рынках, оценка объектов недвижимости, построение профилей потенциальных покупателей определенного товара, анализ продуктовой корзины - вот далеко не полный перечень задач, успешно решаемых с помощью систем интеллектуального и статистического анализа данных.
Системы интеллектуального анализа предназначены для автоматизированного поиска ранее неизвестных закономерностей в имеющихся в распоряжении менеджера данных с последующим использованием полученной информации для подготовки решений. Помимо статистических методов базовыми инструментами анализа в таких системах являются нейронные сети, деревья решений и индукция правил. Однако несмотря на то, что в последние годы рынок программных продуктов этого типа активно развивается, они все еще недоступны по цене предприятиям среднего и малого бизнеса. В то же время компаниям такого размера, как правило, не требуется столь мощный аналитический инструментарий, предлагаемый этими системами.
Более доступными средствами анализа данных на сегодняшний день являются статистические программные продукты (СПП). В мировой практике компьютерные системы статистического анализа и обработки данных широко применяются как в исследовательской работе в области экономики, так и в практической деятельности аналитических, маркетинговых и плановых отделов банков, страховых компаний, производственных и торговых фирм. В последние годы заметно возрос спрос на СПП и в нашей стране.
СПП позволяют решить широкий спектр задач «разведочного» анализа данных, статистического исследования зависимостей, планирования экспериментов, анализа временных рядов, анализа данных нечисловой природы и т.д. Настоящие методические разработки посвящены вопросам корреляционно-регрессионного анализа статистических связей с использованием одного из самых популярных в России статистических программных продуктов - пакета STATISTICA, функционирующего в среде Windows.

Персональные компьютеры открывают статистические методы широкому кругу пользователей, на 90% процентов состоящему из непрофессиональных статистиков. Эти методы стали доступны не теоретически, а в высокоинтегрированных средах, где весь этап анализа от ввода данных, импорта их из других баз данных до построения автоотчетов и сохранения их в формате HTML полностью автоматизирован (вы легко проведете аналогию с организацией современной хирургической операции). Сейчас стало модным ругать компанию Майкрософт и обвинять Б.Гейтса во многих бедах, однако мало кто будет отрицать, что Майкрософт создал удобный стандарт для множества конкретных прикладных программ, в частности для анализа данных. Оказалось, что статистический анализ очень удобно проводить в среде Windows. Эта среда очень естественная для него.

Известно несколько систем, предназначенных для статистического исследования данных: SAS, SPSS, S-плюс, STATISTICA и др. Достоинство STATISTICA состоит в том, что она изначально основана на Windows-технологиях, а не переносилась с больших компьютеров. Можно сказать, что STATISTICA является Windows-средой, предназначенной для всестороннего проведения статистического анализа данных.

Имеются следующие 7 причин, по которым предпочтительнее выбирать STATISTICA среди других систем: во-первых, полная согласованность со стандартами Windows, легкая обучаемость (во многом связанная с реализацией Windows-технологий, отражающих интуитивные представления статистиков о среде анализа данных), минимальные требования к компьютеру, уникальная научная и презентационная графика, исчерпывающий набор классических и современных методов статистики, представленных в системе, полный перевод системы на русский язык и, что немаловажно, цена, которая, благодаря политике компании разработчика, доступна для широкого круга пользователей.

Date: 2015-06-11; view: 4847; Нарушение авторских прав