В теории корреляция решаются две основные задачи: 1)определяют зависимость между случайными величинами в виде формулы; 2)определяют силу и тесноту этой зависимости

Корреляцию подразделяют по направлению, форме и числу связей.

I. По направлению корреляция может быть прямой и обратной.При прямой корреляции с увеличением значения признака х увеличивается значение признака у. При обратной корреляции с увеличением значения признака х, значение признака у уменьшается.II.По форме корреляция бывает линейной и криволинейной.Линейная корреляция имеет место, когда с увеличением признака х соответственно увеличивается признак у. При криволинейной корреляции значение х и у изменяется сначала в одном направлении, затем в противоположном.III. По числу связей корреляция бывает простой, (когда имеется связь между двумя признаками) и множественной (имеется связь трех и более признаков.IV. По силе связи корреляция бывает сильной, средней и слабой.

Если некоторые пары чисел повторяются, можно составить корреляционную таблицу – такую таблицу, в которой результаты наблюдений записываются в порядке возрастания с указанием частот.

Выборочным коэффициентом корреляции называется отношение выборочного корреляционного момента к произведению выборочных средних квадратических отклонений этих величин:

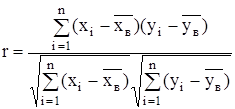
Коэффициент корреляции показывает тесноту и направление связи.

Свойства выборочного коэффициента корреляции:

1. значения коэффициента корреляции изменяются на множестве r 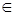[-1;1];

2. чем больше абсолютное значение коэффициента корреляции, тем теснее связь между изученными признаками;

3. если коэффициент корреляции равен 0 (k=0), то между изученными признаками нет линейной корреляционной зависимости,

если |k|=1, то связь полная;

если 0,7<|k|<0,99, то связь сильная;

если 0,3<|k|<0,7, то связь средняя;

если |k|<0,3, то связь слабая.

Если r 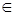[-1;0), то связь обратная;

если r 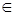(0;1] – зависимость прямая.

Пример: У двенадцати испытуемых, участвующих в эксперименте по заучиванию чисел и слов, были получены следующие результаты: числа (X)5,5,6,3,6,7,2,5,4,3,5,4;

Слова (Y)- 4,3,4,5,4,2,4,33,6,5,6. Найти коэффициент корреляции.

Решение. Составим вспомогательную таблицу:

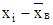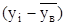
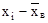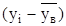
№	Числа (х)	Слова (у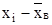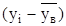)	()		()·	()2	2
			1,58	0,12	0,199	2,49	0,014
			1,58	1,12	0,456	2,49	1,254
			2,58	0,12	0,310	6,65	0,014
			-1,58	1,12	-1,770	2,49	1,254
			2,58	0,12	0,310	6,65	1,254
			3,58	-2,12	-7,58	12,81	4,494
			-2,58	0,12	-0,310	6,65	0,014
			1,58	-1,12	- 1,770	2,49	1,254
			0,58	-1,12	-0,654	0,33	1,254
			-1,58	2,12	-3,330	2,49	4,494
			1,58	1,12	0,456	2,49	1,254
			0,58	2,12	1,230	0,33	4,494
∑					18,375	48,36	21,048

;

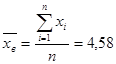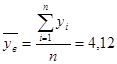
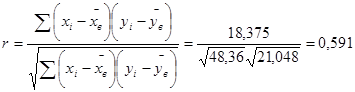
Вывод: Между запоминанием чисел и слов существует средняя прямая связь.

19. О чём говорит положительная и отрицательная связь между признаками?

Коэффициент корреляции(лат. correlatio – соотношение, взаимосвязь) – определяет величину и направление связи между признаками. Величина этого коэффициента (r) выражается в пределах от 0 до ± 1. Наличие знака «+» означает, что между признаками существует положительная корреляция, когда при увеличении одного признака другой также возрастает или, наоборот, при уменьшении одного признака другой также снижается. Если коэффициент корреляции со знаком «-», это указывает на отрицательную (обратную) связь, когда увеличение одного признака сопровождается уменьшением другого.Чем ближе показатель к единице, тем сильнее связь между признаками. При r=0,1-0,3 связь считается слабой, в пределах 0,3-0,5 – умеренной, 0,5-0,7 – заметной, 0,7-0,9 – высокой и 0,9-0,99 – весьма высокой. Например, в опыте установлена умеренная положительная связь (r = +0,36) между скоростью молокоотдачи и суточным удоем коров голландской породы.

20. С какой целью используется коээфициент регрессии и как он расчитывается.

Коэффициенты регрессии показывают интенсивность влияния факторов на результативный показатель. Если проведена предвари­тельная стандартизация факторных показателей, то b ₀ равняется сред­нему значению результативного показателя в совокупности. Коэффици­енты b ₁, b ₂, ..., b_n показывают, на сколько единиц уровень результативно­го показателя отклоняется от своего среднего значения, если значения факторного показателя отклоняются от среднего, равного нулю, на одно стандартное отклонение. Таким образом, коэффициенты регрессии ха­рактеризуют степень значимости отдельных факторов для повышения уровня результативного показателя. Конкретные значения коэффициен­тов регрессии определяют по эмпирическим данным согласно методу наименьших квадратов (в результате решения систем нормальных урав­нений).

Аналитические достоинства регрессионных моделей заключаются в том, что, во-первых, точно определяется фактор, по которому выявля­ются резервы повышения результативности хозяйственной деятельно­сти; во-вторых, выявляются объекты с более высоким уровнем эффек­тивности; в-третьих, возникает возможность количественно измерить экономический эффект от внедрения передового опыта, проведения организационно-технических мероприятий.

При наличии корреляционной связи между факторными и результативными признаками врачам нередко приходится устанавливать, на какую величину может измениться значение одного признака при изменении другого на общепринятую или установленную самим исследователем единицу измерения.

Например, как изменится масса тела школьников 1-го класса (девочек или мальчиков), если рост их увеличится на 1 см. В этих целях применяется метод регрессионного анализа.

Наиболее часто метод регрессионного анализа применяется для разработки нормативных шкал и стандартов физического развития.

1. Определение регрессии. Регрессия — функция, позволяющая по средней величине одного признака определить среднюю величину другого признака, корреляционно связанного с первым.С этой целью применяется коэффициент регрессии и целый ряд других параметров. Например, можно рассчитать число простудных заболеваний в среднем при определенных значениях среднемесячной температуры воздуха в осенне-зимний период.Определение коэффициента регрессии. Коэффициент регрессии — абсолютная величина, на которую в среднем изменяется величина одного признака при изменении другого связанного с ним признака на установленную единицу измерения. Формула коэффициента регрессии. R_у/х = r_ху x (σ_у / σ_x) где R_у/х - коэффициент регрессии; r_ху - коэффициент корреляции между признаками х и у;
(σ_у и σ_x) — среднеквадратические отклонения признаков x и у.

21. Как вычисляют ошибку средней арифметической

Эта ошибка определяется по формуле:
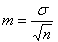,из которой видно, что чем больше разнообразие признака (величина σ), тем больше ошибка. Если бы все объекты были одинаковы, то есть разнообразие было бы равно нулю, то и ошибка была бы равна нулю (m = 0)..Ошибка также зависит от численности выборки n: чем больше численность, тем меньше ошибка. Определив ошибку репрезентативности m, можно найти генеральную среднюю по формул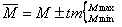е: , где 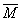– генеральная средняя, M – выборочная средняя, m – ошибка репрезентативности или просто ошибка, t – критерий Стьюдента, соответствующий вероятности получаемого результата.Точное значение генеральной средней найти невозможно, поскольку число объектов стремится к бесконечности. С помощью данной формулы с определенной степенью вероятности находятся две границы: максимального и минимального значений.

22. Как определяют достоверность разницы между выборочными средними арифметическими

Date: 2015-06-11; view: 1745; Нарушение авторских прав