Средняя ошибка малой выборки вычисляется по формуле

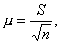(5.14)

где S — оценка среднего квадратического отклонения в генеральной совокупности по малой выборке. Она равна:

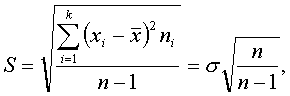
13. Как вычесляется средняя арифматическая в выборках

Определение средних значений изучаемого признака. Как уже отмечалось, зоотехнические опыты являются сравнительными. В них сравнивают между собой группы и периоды, то есть средние величины изучаемых признаков. В зависимости от цели исследования определяют несколько средних величин: среднюю арифметическую, взвешенную среднюю арифметическую, среднюю гармоническую и др.

Средняя арифметическая – наиболее характерное значение признака для данной совокупности (группы), ее математический центр тяжести.

Среднюю арифметическую определяют по формул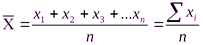е: где – средняя арифметическая, ранее обозначали буквой М; 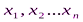– значения признака для каждого члена совокупности (варианты), ранее обозначали буквой V; n – общее число членов совокупности (группы) 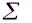(сигма – греческая прописная буква) – знак суммирования.

Например, в группе из 5 коров среднесуточный удой отдельных животных составил, кг: 10,5; 9,7; 13,5; 14,0; 12,3.

Чтобы вычислить среднюю арифметическую для этой группы, подставим данные в вышеприведенную формулу:

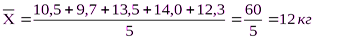
Для больших выборок, когда число особей более 30, раньше применяли непрямой способ вычисления средней арифметической. Для этого предварительно строили вариационные ряды. При использовании компьютеров необходимость в этом отпала.

Основные свойства средней арифметической:

• она характеризует совокупность (группу) в целом, а не отдельных ее членов;
• средняя арифметическая величина абстрактная, то есть может не совпадать ни с одной вариантой и иметь дробную величину. Например, в группе на свиноматку за год получено 1,7 опороса. Но ведь от каждой свиноматки можно получить или один, или два опороса за год;
• среднюю арифметическую применяют для характеристики однородной совокупности. Например, среднюю живую массу определяют по отдельным половозрастным группам.

Взвешенная средняя арифметическаяопределяется, когда разный математический вес признака. Например, требуется определить среднее содержание переваримого протеина в 1 кг смеси, состоящей из 70 кг ячменя и 30 кг гороха, если в 1 кг ячменя содержится 75 г переваримого протеина, а в 1 кг гороха – 210 г.

Взвешенную среднюю рассчитывают по формуле:

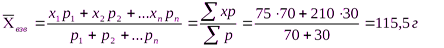
где 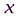– значение признака (варианта);

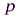– математический вес признака.

Чтобы рассчитать взвешенную среднюю арифметическую, каждое значение признака умножают на его вес, все эти произведения суммируют и полученный результат делят на сумму весов.Взвешенную среднюю применяют в зоотехнии часто, например, при определении процента жира молока за лактацию.

14. Показатели, характеризующие разнообразие признаков

Признаки, или переменные, могут принимать различные конкретные значения.Различают следующие виды признаков:

Качественные или номинальные– не поддающиеся непосредственному измерения, например, характеристики пациента: диагноз, пол, профессия, семейное положение. Качественные данные, которые могут быть отнесены только к двум противоположным категориям да – нет, принимающие одно из двух значений (выжил – умер; курит – не курит)) называются дихотомическими.

Порядковые или ранжируемые – эти признаки можно расположить в естественном порядке (ранжировать), но при этом отсутствует количественная мера расстояния между величинами. Примером являются оценка тяжести состояния пациента, стадия болезни, самооценка состояния здоровья. При этом допускается, что тяжелое течение заболевания «хуже», чем среднетяжелое, а очень тяжелое – «еще хуже», однако нельзя сказать во сколько или на сколько хуже. Можно сказать, что порядковые данные занимают промежуточное положение между количественными и качественными типами. Их можно упорядочить как количественные данные, но над ними нельзя производить арифметические действия, как над качественными данными.

Количественные или интервальные– признаки, количественная мера которых четко определена; наиболее удобный для статистического анализа тип данных.

Количественные признаки могут быть

Непрерывными, принимающими любое значение на непрерывной шкале, например масса тела, температура, биохимические показатели крови;

дискретными, принимающие лишь определенные значения из диапозона измерения, обычно целые, например, число рецидивов, число детей в семье, число заболеваний у одного больного, число выкуриваемых сигарет.

15. Как вычисляется среднее арифметическое отклонение в больших и малых выборках?

Наиболее полную характеристику разнообразия признака в статистической совокупности дает среднее квадратическое отклонение δ, которое является общей мерой отклонения вариант от своей средней.

Расчет среднего квадратического отклонения осуществляется в определенной последовательности и включает пять этапов:

1. Определение средней арифметической (М).2. Расчет истинного отклонения (d) каждой варианты от средней величины (v — M).3. Возведение каждого отклонения в квадрат (d²) (если в исследуемой совокупности некоторые варианты встречаются неоднократно (р>1), следующим шагом необходимо умножить размер отклонения этих вариант, возведенного в квадрат (d²), на их частоту (р)).4. Определение суммы (∑ d² или ∑d²р)5. Расчет среднего квадратического отклонения (по формуле.

Date: 2015-06-11; view: 1456; Нарушение авторских прав