Представление чисел в ЭВМ

В действительности речь пойдет не только о представлении различных чисел собственно в памяти ЭВМ, но вообще об особенностях различных способов записи чисел.

Прежде всего отметим, что любое число – это не реальный, а идеальный объект, абстракция, теоретико-математическое понятие. В материальном мире чисел не существует. Поэтому возникает вопрос: как ЭВМ – реальное техническое устройство – может оперировать с идеальными объектами? Эта возможность обеспечивается представлением чисел с помощью цифр. Цифры – это условные знаки, используемые для обозначения чисел. При этом в качестве цифр могут использоваться реальные объекты (графические символы – при записи на бумаге, сочетания звуков – в устной речи, импульсы электрического тока – в ЭВМ).

Система счисления – это, по существу, набор правил, в соответствии с которыми обозначаются как сами числа, так и действия над ними. В большинстве традиционно используемых систем счисления числа представляются в виде разложения по степеням некоторого заранее выбранного числа, называемого основанием системы счисления. Эти системы называются позиционными, т.к. значение каждой цифры зависит от ее положения в записи числа. Например, запись вида 11 будет означать: в десятичной системе – одиннадцать (один десяток плюс одна единица), в восьмеричной системе – девять (одна восьмерка плюс одна единица), в двоичной системе – три (одна двойка плюс одна единица) и т.д. Здесь две одинаковые цифры имеют разный смысл, более того, значение цифры в старшем разряде зависит от того, какая система счисления используется.

Таким образом, записывая числа с помощью цифр, необходимо прежде всего определить используемую систему счисления. Договоримся основание системы счисления обозначать буквой 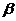. При «ручных» вычислениях традиционно используется десятичная система счисления. Внутри ЭВМ всегда используется двоичная система. Это объясняется тем, что она, имея всего две цифры (0 и 1), наиболее проста для машинной реализации. Однако запись чисел в этой системе очень громоздка (требуется очень большое число разрядов), поэтому при необходимости отобразить машинные вычисления на бумаге используются восьмеричная или шестнадцатеричная системы.

Количество разрядов, отводимых для записи числа, теоретически может быть сколь угодно большим, однако на практике оно всегда ограничено. Причем, если при записи числа на бумаге мы можем менять это количество разрядов в достаточной степени произвольно, то в памяти ЭВМ для хранения всех однотипных (целых, действительных и т.д.) чисел отводится одно и то же строго определенное число разрядов. Договоримся обозначать его буквой t.

И, наконец, значение каждой цифры в записи числа определяется ее положением относительно разделителя (обычно мы его называем десятичной точкой), отделяющего целую часть числа от дробной. При записи числа на бумаге мы просто ставим в нужном месте точку – и все. Когда же речь идет о представлении числа в памяти ЭВМ, «нарисовать» точку невозможно, поэтому надо каким-либо косвенным способом указать ее место в записи числа. Это можно сделать двумя способами. Первый из них называется представлением с фиксированной, а второй – с плавающей точкой.

Представление чисел с фиксированной точкой.

Основная идея заключается в следующем: раз нельзя взять и поставить точку, то давайте заранее договоримся, где именно она находится. Таким образом, для представления чисел в этой форме необходимо определить: основание системы счисления 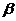, количество разрядов в записи числа 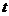и количество разрядов в дробной части числа 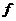. Эти три параметра представления в совокупности определяют множество чисел, представимых в данной форме: .

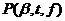Рассмотрим в качестве примера следующее множество представимых чисел: – десятичная система счисления, для записи чисел отводится четыре разряда, из них – один после точки. При этом будем предполагать, что знак числа может быть указан отдельно за пределами отведенных четырех разрядов. Легко видеть, что в такой форме можно представить следующие числа:

-999.9; -999.8; … -001.0; -000.9; … -000.1; 000.0; 000.1; … 001.0; … 999.9

Отсюда следует, что:

- существует такой диапазон чисел, что числа выходящие за его пределы представить в данной форме невозможно;

- внутри этого диапазона точно можно представить только некоторые числа, а все остальные – приближенно;

- числа, точно представимые в данной форме, равномерно заполняют указанный диапазон (расстояние между двумя ближайшими такими числами всегда одно и то же);

- ошибка представления чисел в такой форме – это ошибка округления, и поэтому предельная абсолютная ошибка равна половине единицы младшего разряда в записи числа и не зависит от величины самого числа; при этом предельная относительная ошибка уменьшается с увеличением модуля числа.

Необходимо отметить, что на практике действительные числа в такой форме не представляются. И используется эта форма для представления в ЭВМ целых чисел. При этом система счисления – двоичная, для записи целого числа отводится 4 байта, т.е. 32 двоичных разряда, один из которых – знаковый (остается 31 разряд для числа). Разрядов для дробной части – нет. Таким образом, множество представимых чисел – это 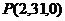и наибольшее (по модулю) число равно 2³¹– 1=2147483647.

Представление чисел в форме с плавающей точкой.

Так как при умножении и делении на одно и то же число результат не меняется, то почти любое число (кроме нуля) можно привести к виду 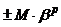, где 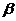– основание используемой системы счисления, 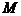– нормализованная мантисса, удовлетворяющая условию 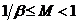, 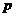– порядок числа. При этом запись числа состоит из двух частей: мантиссы и порядка. Подразумевается, что точка стоит непосредственно перед первой значащей цифрой мантиссы Порядок же показывает, на сколько знаков влево или вправо нужно сдвинуть точку, чтобы из мантиссы получить исходное число. Это представление чисел характеризуется четырьмя параметрами: основанием системы счисления 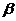, количеством разрядов мантиссы 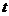, минимальным 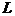и максимальным 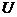значениями порядка. Эти параметры определяют множество представимых чисел: 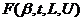. Рассмотрим, например, множество чисел, представимых в форме 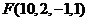. Очевидно, что оно включает в себя числа:

±[0.]10×10^-1,±[0.]11×10^-1,…,±[0.]99×10^-1,±[0.]10×10⁰,…,±[0.]99×10⁰,±[0.]10×10¹,…,±[0.]99×10¹,
т.е. в привычной записи: ±0.010, ±0.011,…, ±0.099, ±0.10, ±0.11,…, ±0.99, ±1.0, ±1.1,…, ±9.9

К такому набору чисел обычно искусственно добавляется ноль, записываемый в форме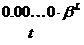

Отсюда следует, что:

- существует такой диапазон чисел, что числа, выходящие за его пределы, представить в данной форме невозможно;

- внутри этого диапазона точно можно представить только некоторые числа, а все остальные – приближенно;

- числа, точно представимые в данной форме, неравномерно заполняют указанный диапазон (расстояние между двумя ближайшими такими числами растет по мере приближения к границам диапазона);

- предельная абсолютная ошибка представления чисел в такой форме – это ошибка округления, равная 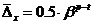, зависит от величины самого числа; при этом предельная относительная ошибка 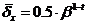от величины числа не зависит.