Моделирование случайной величины с произвольным законом распределения

В основе моделирования случайных величин с произвольными законами распределения вероятностей лежит, как правило, метод обратной функции.

В этом методе используется следующая теорема.

Теорема. Если случайная величина 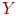имеет плотность распределения вероятностей 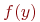, то распределение случайной величины

(y)dy)

равномерно в интервале 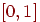, т. е.

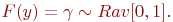
По определению, 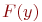является функцией распределения случайной величины .

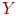Теорема может быть проиллюстрирована графиками, представленными на рис. 3.10.

Обозначим: - -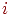е число из 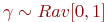, 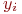- -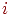е случайное число из произвольного распределения.

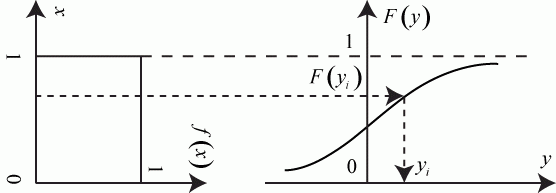
Рис. 3.10. Иллюстрация к методу обратной функции Из (3.1) следует:

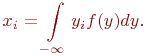
Моделировать равномерно распределенное случайное число 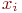мы уже умеем. Нужно найти неизвестное 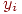, находящееся в верхнем пределе интегрирования.

Относительно 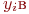ыражение принимает вид:

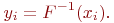
Отсюда и название - "метод обратной функции".

Пример 3.6. Получить формулу для моделирования случайных

чисел, распределенных по экспоненциальному закону, с параметром (матожиданием ).

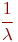Плотность 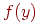и функция 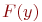этого распределения имеют вид (рис. 3.11):

Решение

Поскольку случайная величина 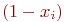имеет равномерное распределение в интервале 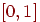, как и , то справедливо:

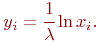
Примеров подобного аналитического преобразования случайного числа в случайное число из произвольного распределения немного, так как для многих законов распределения, встречающихся в практике моделирования, интеграл (3.1) относится к неберущимся, а численные методы решения увеличивают затраты машинного времени.

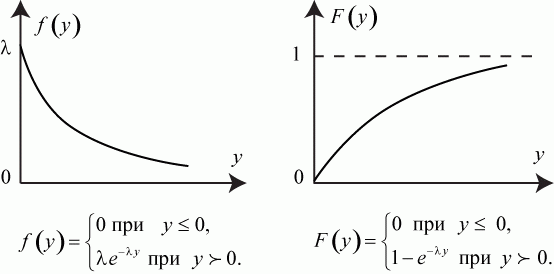
Рис. 3.11. Плотность и функция экспоненциального распределения

Поэтому в современных системах моделирования применяется приближенный метод обратной функции, основанный на кусочно-линейной аппроксимации функции распределения моделируемой случайной величины.

Суть метода заключается в следующем.

Требуемый закон распределения случайной величины размещается в памяти компьютера в виде координат функции распределения. Каждая координата состоит из случайного числа 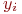и соответствующего значения функции распределения :

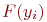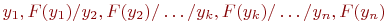
Чем больше координат, тем точнее будет моделирование. Приемлемая точность обеспечивается заданием 20…30 координат.

При обращении за очередным случайным числом нужного закона распределения сначала генерируется случайное число из 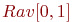. Это число сравнивается со значениями .

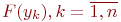При совпадении выдается соответствующее случайное число .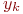

Если нет совпадения, то случайное число 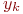вычисляется из подобия треугольников, как показано на рис. 3.12.

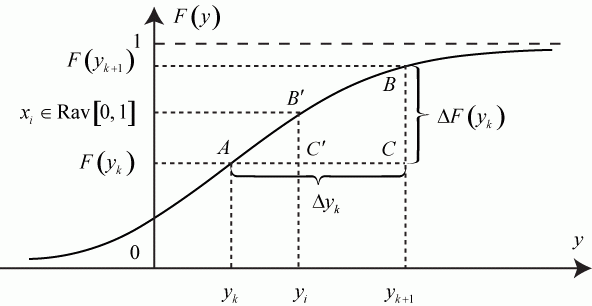
Рис. 3.12. Иллюстрация к методу кусочно-линейной аппроксимации

Из подобия треугольников ABC и AB'C' следует:

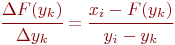
Отсюда по находится значение .

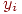Значительную роль в моделировании играет случайная величина, имеющая нормальное распределение. Метод обратной функции в аналитическом виде здесь неприемлем, так как интеграл (3.1) неберущийся, а его численное решение громоздко.

Для генерации случайных чисел, подчиненных нормальному распределению, применяется метод обратной функции с кусочно-линейной аппроксимацией, а также метод, основанный на центральной предельной теореме (ЦПТ) теории вероятностей.

Как известно, ЦПТ дает теоретическое объяснение подтвержденному практикой наблюдению: если исход случайного события определяется большим числом случайных факторов, и влияние каждого фактора мало, то такой случайный исход хорошо аппроксимируется нормальным распределением. Эта теорема имеет много формулировок. Одна из наиболее практичных для целей моделирования случайных последовательностей - теорема Леви-Линдеберга.

Теорема. Случайная величина

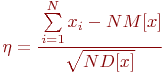
где 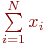- сумма случайных чисел одного и того же распределения с матожиданием 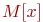и дисперсие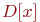й при асимптотически стремится к нормальному распределению с 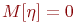и дисперсией .

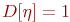Удобно случайные числа брать из рассмотренного датчика 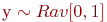. В этом случае , .

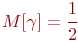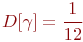Хорошее приближение к нормальному распределению получается уже при числе 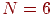. Каждое случайное число при 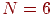генерируется так:

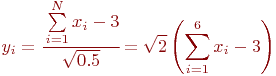
Недостаток способа состоит в том, что он не экономичен, так как для генерирования одного случайного числа 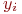требуется шесть случайных чисел из распределения .

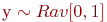В ряде случаев применяют датчики с числом 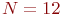. Тогда

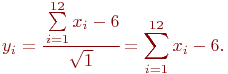
Если датчик случайных чисел нормального распределения выдает стандартную последовательность чисел с 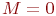, , 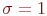то пересчет на произвольное значение характеристик выполняется так:

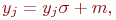
где 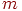- требуемое значение матожидания;

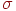- требуемое значение среднего квадратического отклонения;

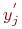- случайное число из нормального распределения с математическим ожиданием 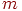и средним квадратическим отклонением .

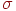В современных системах моделирования имеются встроенные датчики, позволяющие непосредственного задавать нужную случайную величину с требуемыми значениями характеристик. Однако если исследователя эти возможности не удовлетворяют (например, по точности представления функции распределения вероятностей), то он может задать требуемый закон распределения самостоятельно.

Date: 2015-07-17; view: 513; Нарушение авторских прав