Статистическое моделирование при решении детерминированных задач

Метод статистических испытаний может быть использован как численный метод решения математических задач. Именно в таком качестве он был применен в США в 1944 г. Джоном фон Нейманом при расчетах по созданию ядерного реактора.

Применение метода рассмотрим на примере вычисления некоторого интеграла.

Пример 3.4. Пусть , 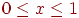. Полагаем, что функция такова, что интеграл относится к "неберущимся".

Требуется вычислить .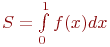

Решение

Представим функцию в координатах и 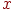как показано на рис. 3.7. Как известно, численное значение интеграла данного вида равно площади 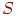. Площадь 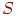состоит из множества элементарных площадок - точек. Количество точек в этой площади и будет численным значением искомого интеграла.

Имитируем координаты каждой точки значениями и 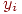, принадлежащими равномерному распределению на участке :

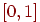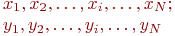
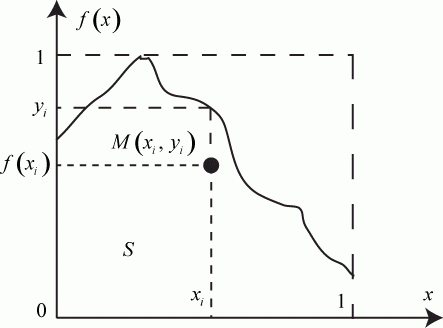
Рис. 3.7. Вычисление интеграла

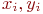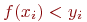Рассмотрим пару чисел . Вычислим и сравним с . Если , то это означает, что точка 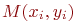принадлежит площади 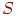. Если 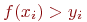, то это означает, что точка 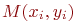не принадлежит площади .

Введем:

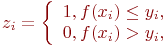
Число точек, попавших в границы 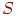равно 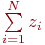, где - общее число точек, попавших в единичную площадь существования функции и аргумента. Отсюда следует:

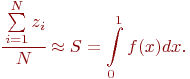
Чем больше будет элементарных площадей - точек, тем точнее будет вычислен интеграл. Приведенное решение примера справедливо для единичных областей существования функции и аргумента. Однако это несущественно, так как произвольные границы существования 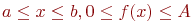заменой переменных можно свести к единичным границам.

Известны статистические алгоритмы численного решения многократных интегралов.

Пример 3.5. Найти оценку интеграла .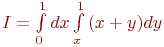

Решение

Область интегрирования ограничена линиями 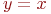, , 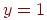, 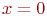т. е. принадлежит единичному квадрату (рис. 3.8).

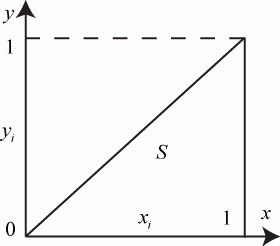
Рис. 3.8. Иллюстрация к примеру 3.5

Площадь области интегрирования (прямоугольного треугольника) 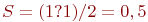. Используем формулу

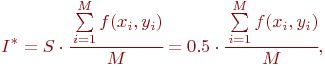
в которой 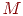- число случайных точек 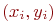, принадлежащих области интегрирования. У этих точек 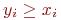. Если данное условие выполняется, то вычисляется

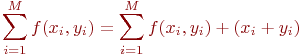
а число случайных точек 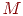увеличивается на : .

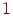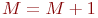Результаты моделирования приведены в табл. 3.2.

Из данных табл. 3.2 (верхние пять строк) видно, что с увеличением числа реализаций ошибка 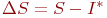в определении оценки интеграла 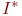уменьшается и при 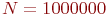становится равной нулю.

Таблица 3.2. Результаты моделирования примера 3.5
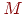
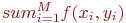
	4,773	487,695	5006,152	49533,242	500191,650
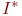
	0,477	0,488	0,497	0,499	0,500
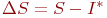
	0,023	0,012	0,003	0,001
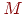
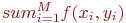
	5,025	494,593	4917,236	49802,019
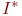
	0,419	0,492	0,498	0,500
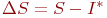
	0,081	0,008	0,002

В четырех нижних строках табл. 3.2 приведены результаты моделирования с другими начальными числами генераторов равномерно распределенных случайных чисел. Как видно, ошибка в оценке интеграла равна нулю уже при 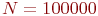реализаций модели.

В заключение отметим, что имитационное (статистическое) моделирование целесообразно применять в случаях:

• когда нет законченной математической постановки задачи;
• когда нет аналитических методов решения сформулированной задачи;
• когда аналитические методы есть, но они не удовлетворяют требованиям точности и достоверности;
• когда аналитические методы есть, но их вычислительные процедуры сложны даже для компьютера;
• когда реализация известных процедур сталкивается с недостаточной математической подготовкой исследователя;
• когда исследователю нужно знать не только оценки искомых характеристик, но и динамику всего случайного процесса.

Date: 2015-07-17; view: 471; Нарушение авторских прав