
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Начальный и центральный теоретические моменты
|
|
Содержание
§ Начальные и центральные теоретические моменты.2стр.
§ Обычные, начальные и центральные эмпирические
моменты.4стр.
§ Условные эмпирические моменты. Отыскание центральных моментов по условным.5стр.
§ Метод моментов для точечной оценки параметров распределения.6стр.
§ Примеры решения задач.8стр.
§ Практическая часть.9стр.
§ Список использованной литературы.17стр.
Начальный и центральный теоретические моменты.
Рассмотрим дискретную случайную величину Х, заданную законом распределения:
Х 1 2 5 100
Р 0.6 0.2 0.19 0.01
Найдем математическое ожидание Х:
М(Х) = 1*0.6 + 2*0.2 + 5*0.19 + 100*0.01 = 2.95
Напишем закон распределения 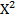 :
:
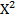 1 4 25 10000
1 4 25 10000
Р 0.6 0.2 0.19 0.01
Найдем математическое ожидание 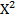 :
:
М(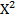 ) = 1*0.6 + 4*0.2 + 25*0.19 +10000*0.01 = 106.15
) = 1*0.6 + 4*0.2 + 25*0.19 +10000*0.01 = 106.15
Видим, что М(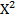 ) значительно больше М(Х). Это объясняется тем, что после возведения в квадрат возможное значение величины
) значительно больше М(Х). Это объясняется тем, что после возведения в квадрат возможное значение величины 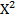 , соответствующее значению х=100 величины Х, стало равным 10000, т.е. значительно увеличилось; вероятность же этого значения мала (0.01).
, соответствующее значению х=100 величины Х, стало равным 10000, т.е. значительно увеличилось; вероятность же этого значения мала (0.01).
Таким образом, переход от М(Х) к М(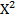 ) позволил лучше учесть влияние на математическое ожидание того возможного значения, которое велико и имеет малую вероятность. Разумеется, если бы величина Х имела несколько больших и маловероятных значений, то переход к величине
) позволил лучше учесть влияние на математическое ожидание того возможного значения, которое велико и имеет малую вероятность. Разумеется, если бы величина Х имела несколько больших и маловероятных значений, то переход к величине 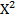 , а тем более к величинам
, а тем более к величинам  ,
, 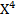 и т.д., позволил бы еще больше «усилить роль» этих больших, но маловероятных возможных значений. Вот почему оказывается целесообразным рассматривать математическое ожидание целой положительной степени случайной величины (не только дискретной, но непрерывной).
и т.д., позволил бы еще больше «усилить роль» этих больших, но маловероятных возможных значений. Вот почему оказывается целесообразным рассматривать математическое ожидание целой положительной степени случайной величины (не только дискретной, но непрерывной).
Начальным моментом порядка k случайной величины Х называют математическое ожидание величины 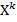 :
:
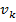 =M(
=M(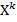 )
)
В частности,
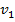 = М(Х),
= М(Х), 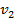 = M(
= M(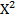 )
)
Пользуясь этими моментами, формулу для вычисления дисперсии D(X) = M(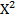 ) -
) - 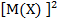 можно записать так:
можно записать так:
D(X) = 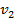 -
- 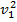 (*)
(*)
Кроме моментов случайной величины Х целесообразно рассматривать моменты отклонений Х – М(Х).
Центральным моментом порядка k случайной величины Х называют математическое ожидание величины 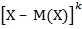 :
:
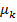 = M
= M 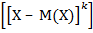 .
.
В частности,
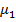 = М
= М 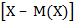 = 0 (**)
= 0 (**)
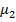 = M
= M 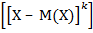 = D(X) (***)
= D(X) (***)
Легко выводятся соотношения, связывающие начальные и центральные моменты. Например, сравнивая (*) и (***), получим
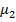 =
= 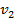 -
- 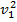 .
.
Нетрудно, исходя из определения центрального момента и пользуясь свойствами математического ожидания, получить формулы:
 =
= 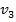 - 3
- 3  + 2
+ 2 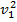 ,
,
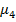 =
= 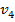 - 4
- 4 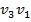 + 6
+ 6 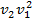 - 3
- 3 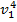 .
.
Моменты более высоких порядков применяются редко
Замечание. Моменты, рассмотренные здесь, называют теоретическими. В отличие от теоретических моментов, моменты, которые вычисляются по данным наблюдений, называются эмпирическими. Определения эмпирических моментов рассмотрим далее.
Date: 2015-07-17; view: 1125; Нарушение авторских прав