
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Понятие численного интегрирования. Нахождение интеграла методом прямоугольников, методом трапеций, методом Симпсона
|
|
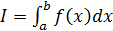 . Геометрический смысл: если ф-я непрерывна на
. Геометрический смысл: если ф-я непрерывна на 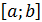 , и мы можем найти её первообразную F, то используется формула Ньютона-Лейбница
, и мы можем найти её первообразную F, то используется формула Ньютона-Лейбница 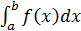 =F(b)-F(a). Но дело в том, что:
=F(b)-F(a). Но дело в том, что:
1. F можно определить только для узкого круга ф-ций
2. Затраты на получение F(x) мб очень велики
3. Ф-я f(x) мб задана таблично
Поэтому используется численное интегрирование.
Пусть f(x) – вещественная ф-я, определенная на 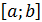 , разобьем её на интервалы
, разобьем её на интервалы 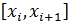 ,
, 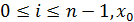 =a,
=a, 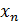 =b
=b
На каждом маленьком инт выберем  ,
,  , и составим сумму:
, и составим сумму: 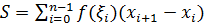 .
. 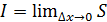 , если предел существует.
, если предел существует.
Сумма S без предела – пример численного интегрирования, поскольку сумма отличается от истинного значения интеграла, можем оценить
 ,
, 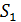 и
и 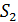 - верхняя и нижняя суммы Дарбу,
- верхняя и нижняя суммы Дарбу, 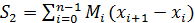 ,
,  .
.
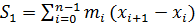 ,
, 
Формул числ.интегрирования много, они отличаются друг от друга:
1) Выбором точек  и
и 
2) Скоростью сходимости
3) Оценкой погрешности
В общем случае точки  - узлы, а разность между
- узлы, а разность между 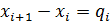 - весы, весы не зависят от f(x). Тогда можно составить:
- весы, весы не зависят от f(x). Тогда можно составить:  )
)
S=Q+R, R – погрешность вычисления интеграла, квадратурная формула. Считается, что она задана, если известно, как выбираются узлы в весах, и как считается погрешность R.
Метод прямоугольников.
Отрезок 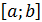 разбиваем на отрезки с шагом h, получаем набор
разбиваем на отрезки с шагом h, получаем набор 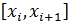 , f(x) принадлежит с2
, f(x) принадлежит с2 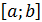 (дважды дифференцируема)
(дважды дифференцируема)

|

|
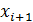
|
| f(x) |
| F |
| C |
| G |
| A |
| B |
| D |
Каждый 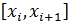 разбивается пополам и берем точку
разбивается пополам и берем точку 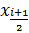 , строим в этой точке прямую и находим точку её пересечения с f(x), проводим прямую FG, заменяем площадь ABCD на площадь AFGD. Мы можем записать:
, строим в этой точке прямую и находим точку её пересечения с f(x), проводим прямую FG, заменяем площадь ABCD на площадь AFGD. Мы можем записать: 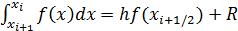
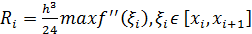 ,
, 
От маленького отрезка можно перейти к 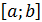 ,
, 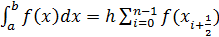 +
+ 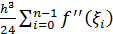
R= 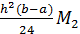 ,
, 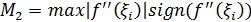
Чем меньше шаг, тем выше точность.
Метод трапеций.
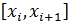 ,
, 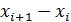 =h>0, f(x) принадлежит с2
=h>0, f(x) принадлежит с2 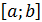 (дважды дифференцируема)
(дважды дифференцируема)
| B |
| C |
| A |
| D |

|
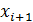
|
На каждом отрезке 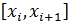 строим хорду BC и площадь крив.тр ABCD заменяем на площадь прямоуг.тр ABCD.
строим хорду BC и площадь крив.тр ABCD заменяем на площадь прямоуг.тр ABCD. 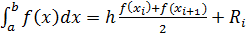
R= 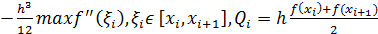
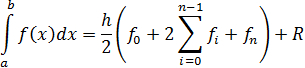
R= 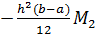 ,
, 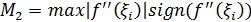
Метод Симпсона.
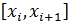 ,
, 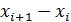 =h>0, f(x) принадлежит с4
=h>0, f(x) принадлежит с4 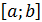
| С |
| В |
| D |
| f(x) |
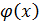
|
| A |

|
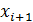
|
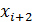
|
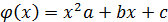
Строим 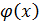 , к-ая в т. В,С,D совподает со знач f(x). Криволинейная трапеция со знач f(x) заменяем на криволинейную трапецию с
, к-ая в т. В,С,D совподает со знач f(x). Криволинейная трапеция со знач f(x) заменяем на криволинейную трапецию с 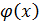 , вычисляем площадь новой криволинейной трапеции.
, вычисляем площадь новой криволинейной трапеции. 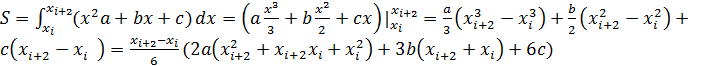
Для тог, чтобы посчитать a,b,c вычислим:

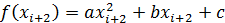
f( 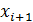 ) =
) = 
Значения должны совпадать с 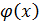 .
.
Составим сумму:
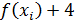 f(
f( 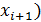 +
+ 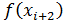 =
= 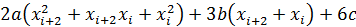 /
/
Отсюда можем записать 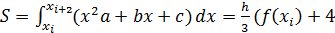 f(
f( 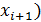 +
+ 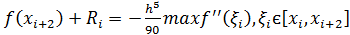
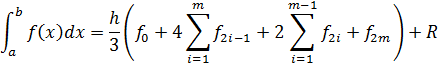
R= 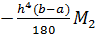 ,
, 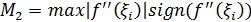
На практике при выборе h для достаточно большого [a;b] необходим о выбрать максимальное знач шага таким образом,чтобы мы смогли вычислить площадь с заданной точностью.
Метод прямоугольника:
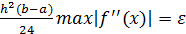
Метод трапеции:
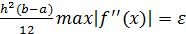
Метод Сипсона:
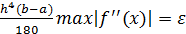
В зав-ти от 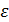 считаем h. Это знач h выбирается исходя из нахудшего поведения f(x) на
считаем h. Это знач h выбирается исходя из нахудшего поведения f(x) на 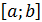
11.Решение обыкновенных дифференциальных уравнений. Методы решения. Задача Коши. Краевая задача. Решение ОДУ методом Эйлера, модифицированным методом Эйлера, методом Рунге – Кутта, методами прогноза и коррекции. Решение ОДУ большого порядка. Решение систем ОДУ. Методы решения краевых задач.
Ур-ния, содержащие неизвестную ф-цию под знаком производной, называются дифференциальными уравнениями. Если ур-ние содержит одну независимую переменную и производную по ней, то оно называется обыкновенным, т.е. ОДУ. Решить ОДУ – это значит найти некоторую ф-цию, которая удовлетворяла бы как самому ур-нию, так, возможно, дополнительным условиям.
В зависимости от дополнительных условий различают задачу Коши и краевую задачу.
Для решения задачи Коши существует набор хорошо апробированных методов, а решение каждой отдельной краевой задачи может потребовать специфических подходов. Поэтому в классической вычислительной математике рассматривают вычисления задачи Коши, которую в простейшем случае можно рассмотреть следующим образом:
Задано ОДУ первого порядка: 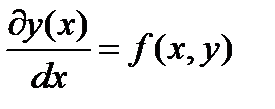 и начальное условие: y(x0)=y0. Требуется найти ф-цию, удовлетворяющую как уравнению, так и начальному условию.
и начальное условие: y(x0)=y0. Требуется найти ф-цию, удовлетворяющую как уравнению, так и начальному условию.
Решение: 1).x1=x0+h; 2)tgα=f(x0,y0); 3)y=y0=tgα(x-x0); 4)x=x1, y=y1; 5)x1y1
Численные методы для решения этой задачи могут быть разбиты на две группы: одношаговые и многошаговые.
Date: 2015-07-17; view: 545; Нарушение авторских прав