
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Решение нелинейных уравнений. Отделение корней. Метод половинного деления. Метод хорд. Метод касательных
|
|
Нелинейное ур-е (НУ) в общем виде y=f(x), f(x;y)=0, x є 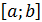
Нахождение корней НУ делится на 2 этапа:
1. Отделение корней
2. Уточнение корней
Корень ур-я f(x;y)=0 считается отделенным на 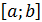 , если на этом отрезке содержится ровно 1 корень данного ур-я. Т.о., отделить корни – значит разбить всю ОДЗ на отрезки, в каждом из к-х существует только 1 корень. Аналитически для нахождения корня исп. теоремы из мат.анализа:
, если на этом отрезке содержится ровно 1 корень данного ур-я. Т.о., отделить корни – значит разбить всю ОДЗ на отрезки, в каждом из к-х существует только 1 корень. Аналитически для нахождения корня исп. теоремы из мат.анализа:
Теорема 1: если f(x) непрерывна на 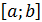 и f(a)*f(b)<0, то внутри
и f(a)*f(b)<0, то внутри 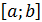 сущ.по крайней мере 1 корень ур-я f(x;y)=0.
сущ.по крайней мере 1 корень ур-я f(x;y)=0.
Теорема 2: если f(x) непрерывна и монотонна на 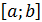 и f(a)*f(b)<0, то внутри этого отрезка содержится корень ур-я f(x)=0, и при том только 1.
и f(a)*f(b)<0, то внутри этого отрезка содержится корень ур-я f(x)=0, и при том только 1.
Отсюда следует, что если на концах отрезка знаки разные, то существует хотя бы 1 корень. В том случае, если знаки одинаковы, то возникают след варианты:
1. Касание (1 корень либо их нечетное кол-во)
2. Кривая не пересекает ось, корней нет.
3. Внутри отрезка ф-я пересекает ось Х четное кол-во раз
Отделение корней:
1) 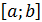 разбивается на n частей, причем n дб достаточно большое, чтобы отрезки разбиения были малы
разбивается на n частей, причем n дб достаточно большое, чтобы отрезки разбиения были малы
2) Рассматриваются все маленькие отрезки и определяются те отрезки, на концах которых функция имеет разные знаки. В случае, если знак одинаковый, вычисляется 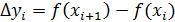 . Такая же разность вычисляется для след уч-ка. Если для этих двух разностей выполняется:
. Такая же разность вычисляется для след уч-ка. Если для этих двух разностей выполняется: 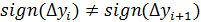 , то мы предполагаем, что на уч-ке
, то мы предполагаем, что на уч-ке 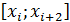 существует корень типа касание. В этом случае мы проверяем величину значения ф-ции
существует корень типа касание. В этом случае мы проверяем величину значения ф-ции 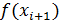 . Если оно мало, т.е.
. Если оно мало, т.е. 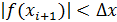 , то в этом случае мы считаем, что
, то в этом случае мы считаем, что 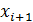 - корень ур-я.
- корень ур-я.
| a\\\\\\\\\\\ |
| c |
| b |
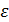 , известно, что корень отделен на
, известно, что корень отделен на 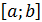 . Можно считать, что a,b-первые приближенные зн-я корня, a – значение с недостатком, b – с избытком. Необходимо уменьшить
. Можно считать, что a,b-первые приближенные зн-я корня, a – значение с недостатком, b – с избытком. Необходимо уменьшить 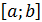 для решения задачи, чтобы длина
для решения задачи, чтобы длина 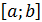 не превышала
не превышала 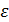 . В этом случае в кач-ве корня ур-я можно взять любую точку из
. В этом случае в кач-ве корня ур-я можно взять любую точку из 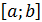 .
.
Метод половинного деления.
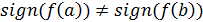
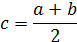
f(c)=0 => с-корень, если нет, то 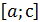 ,
, 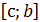 , из них берем тот, на кот-м f(a)*f(c)<0 или f(c)*f(b)<0. Обозначим новый отрезок как
, из них берем тот, на кот-м f(a)*f(c)<0 или f(c)*f(b)<0. Обозначим новый отрезок как 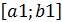 , находим с1 – середину и т.д. Таким образом строится итерационный пр-с, к-й заканчивается в том случае, когда
, находим с1 – середину и т.д. Таким образом строится итерационный пр-с, к-й заканчивается в том случае, когда 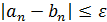 , тогда за корень ур-я
, тогда за корень ур-я
 , погрешность данного метода не превышает
, погрешность данного метода не превышает  ,
, 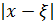 <
< 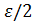
Метод хорд.
| a |
| c |
| b |
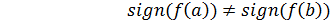
Шаг1. Строим стягивающую хорду между точками пересечения прямой x=a и f(x), x=b и f(x), ур-е хорды:
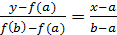 - эта прямая пересекает ось х в т.с
- эта прямая пересекает ось х в т.с
Чтобы найти координату с нужно: 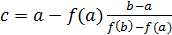
Шаг 2. Таким образом разделили отрезок на 2, выбираем из них тот, где ф-я на концах имеет разные знаки, концы обозначаем 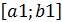 , и для него проделываем те же самые процедуры, получаем
, и для него проделываем те же самые процедуры, получаем 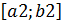 , строим итерационный процесс, к-й продолжается до тех пор, пока не будет выполнено след условие:
, строим итерационный процесс, к-й продолжается до тех пор, пока не будет выполнено след условие: 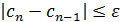 , x=cn. Погрешность метода:
, x=cn. Погрешность метода:
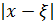 <
< 
Метод касательных. 
1. определим точку пересечения х=А и f(x). Из этой точки ф-ции строим касательную, ур-е которой: 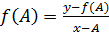 . Отсюда можно найти точку пересечения касательной с осью Х – т. А1.
. Отсюда можно найти точку пересечения касательной с осью Х – т. А1.
2. Ищем точку пересечения прямой х=А1 и f(x), из этой точки строим касательную к f(x) и вычисляем точку её пересечения с осью ОХ\
3. Итерационный пр-с выполняется до тех пор, пока 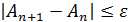 , x=
, x= 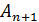 .
.
Для метода касательных характерно, что мы приближаемся к истинному значению корня только с одной стороны.
Погрешность: 
Решение систем нелинейных уравнений. Метод итерации, условие сходимости. Методы спуска. Метод покоординатного спуска. Метод градиентного спуска. Метод наискорейшего градиентного спуска. Метод Ньютона.
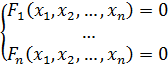 F(
F(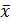 )=0
)=0
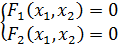 =>
=> 

Первый этап: приближенные значения корней
Второй этап: уточнение корней.
Метод итерации:
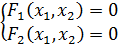 начальные значения корня (
начальные значения корня ( )
)
Пускай к-либо способом мы преобразовали ур-е. начальное приближение мы подставляем в правую часть, получаем:
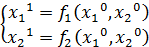 =>
=> 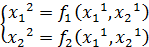 =>
=> 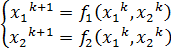
Строим итерационный пр-с, к-й сходится к решению в том случае, если все собственные числа |A|<1.
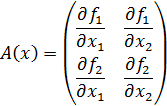
Более слабое условие: сумма модулей коэф-тов столбцов дБ меньше 1.
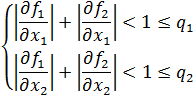
Этот ит пр-с заканчивается в том случае, когда разность между всеми неизвестными на (k+1)-шаге и на к-м шаге не будет превосходить заданного значения 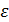 и за решение можно взять решение, найденное на к+1 шаге.
и за решение можно взять решение, найденное на к+1 шаге.
Погрешность решения можно оценить с пом формулы:
 , M=max(
, M=max(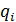 )
)
Методы спуска:
Для всех этих методов характерно наличие ф-ции f такой, что при переходе от одной точки решения x0 к след x1 значение f уменьшится.
Ф-я Ф-целевая ф-я и многие задачи по решению СНАУ сводятся к нахождению Ф.

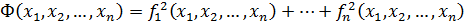
Можно заметить, что при значениях переменных xi, явл корнями системы, Ф=0. Это происходит только в идеальном случае. Для приближенного решения надо найти min Ф(х) на области определения. Задача по решению СНАУ сводится к задаче поиска экстремума ф-ции. Таким образом, идея методов спуска в том, чтобы из начальной точки 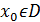 перейти в
перейти в 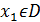 таким образом, чтобы зн-я Ф уменьшилось. Этот итерационный пр-с можно повторять, но на каждом шаге зн-е Ф д уменьшаться. Этот ит пр-с заканчивается, когда
таким образом, чтобы зн-я Ф уменьшилось. Этот итерационный пр-с можно повторять, но на каждом шаге зн-е Ф д уменьшаться. Этот ит пр-с заканчивается, когда 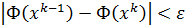 . За решение можно взять вектор
. За решение можно взять вектор 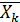 .
.
Метод покоординатного спуска:
Из исходной СНАУ составляем Ф и дано 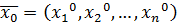
1. Фиксируем все переменные, кроме 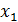 , и находим min Ф на ООФ по переменной
, и находим min Ф на ООФ по переменной 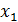 . Новое значение переменной
. Новое значение переменной 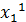 : Ф
: Ф  . Значение Ф(
. Значение Ф(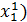 уменьшилось, тк искали min Ф по координате
уменьшилось, тк искали min Ф по координате 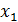 .
.
2. Фиксируем все пер, кроме 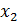 , находим min
, находим min 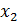 в ООФ, находим
в ООФ, находим 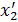 , так делаем n шагов. Перейдем от
, так делаем n шагов. Перейдем от 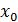 к
к 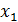 : Ф
: Ф 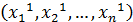 и значение Ф в
и значение Ф в 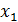 уменьшилось.
уменьшилось.
Аналогично поступая, находим  . Ф(
. Ф(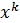 )
) 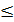 Ф(
Ф(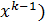 , делаем так, пока
, делаем так, пока 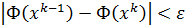 . За решение берем вектор
. За решение берем вектор 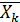 .
.
Метод градиентного спуска:
Градиент – это вектор, к-й имеет направление нормали к пов-ти уровня Ф(x)=const в сторону возрастания ф-ции. 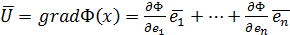
Нам задано приблизительно 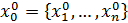 , выбираем шаг h>0. Строим ит пр-с:
, выбираем шаг h>0. Строим ит пр-с: 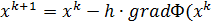 ). Поскольку стоит минус, то будем переходить в сторону убывания ф-ции, на каждом шаге зна-е Ф уменьшается. Так до тех пор, пока
). Поскольку стоит минус, то будем переходить в сторону убывания ф-ции, на каждом шаге зна-е Ф уменьшается. Так до тех пор, пока 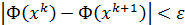
Метод наискорейшего градиентного спуска:
На каждой итерации меняется значение шага h. Можно определить зн-е Ф слева и справа. 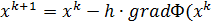 )
)
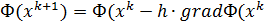 ))
))
Для того, чтобы на каждой итерации h был max возможным, необходимо, чтобы на этой итерации значение Ф max уменьшалось. 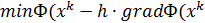 )).На каждой итерации получается свое значение шага.
)).На каждой итерации получается свое значение шага.
Метод Ньютона:
Для этого метода х0 дб достаточно приближенным к решению.
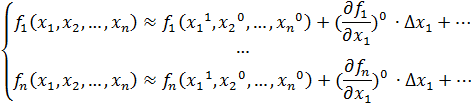
Это разложение подставляем вместо исходной ф-ции

Если исходные нелинейные ур-я были относительно 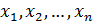 , то преобразованную систему мы получили относительно
, то преобразованную систему мы получили относительно 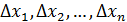 .
.
Системе в матричном виде относительно вектора 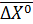 :
:  - линейная система.
- линейная система.
Получаем вектор перехода к нелин системе.
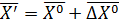 - начальная точка для следующей итерации.
- начальная точка для следующей итерации.
За решение исх системы берем 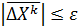
9. Понятие интерполяции. Виды интерполяции. Конечные и разделенные разности. Их свойства и применение. Интерполяция параболическими полиномами по методу Ньютона и методу Лагранжа. Понятие сплайн – интерполяции. Интерполяция сплайнами второго порядка.
Интерполяция – это построение достаточно простой для вычисления ф-ции f(x), совпадающей в узлах со значениями исходной ф-ции f(x), а в остальных точках отрезка [a,b] приближенно представляющая функцию с заданной точностью.
Различают в зависимости от решаемых задач несколько классов интерполяции ф-ции.
Дана f(x): 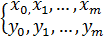
Нужно построить 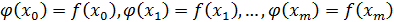
1) Параболическая интерполяция
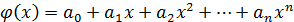
В основе применения лежит теорема Вейерштрасса: если f(x) непрерывна на [a,b],то для любого сколь угодно малого 𝛆 существует полином 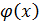 , такой что для любого х
, такой что для любого х 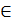 [a,b]:
[a,b]: 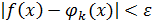
В данном случае задача сводится к поиску полинома наименьшей степени k и требуемой точности совпадения.
Самый простой путь поиска коэффициентов: 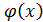 ищем в виде полинома. Для каждой заданной точки составляем равенство искомого полинома и значения ф-ции в узле. Получаем СЛАУ, при этом степень полинома должна соответствовать кол-ву уравнений +1.
ищем в виде полинома. Для каждой заданной точки составляем равенство искомого полинома и значения ф-ции в узле. Получаем СЛАУ, при этом степень полинома должна соответствовать кол-ву уравнений +1.
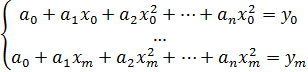
2) Интерполяция тригонометрическими полиномами
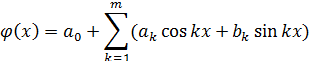
m-порядок полинома.
3) Интерполяция показательными полиномами
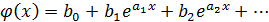
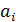 - постоянная времени
- постоянная времени
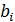 - придаточный коэф-т
- придаточный коэф-т
Для поиска степени искомого полинома используем конечные разности.
Ф-я f(x) задана таблично, узлы - равноотстающие конечные разности 1-го порядка.
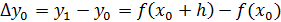
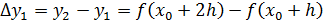
…
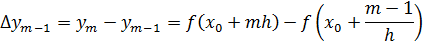
Конечных разностей первого порядка на 1 меньше кол-ва узлов.
Конечные разности 2-го порядка:
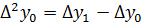
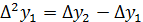
Конечные разности k-го порядка:
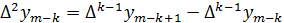
Свойства конечных разностей:
1. Конечные разности константы=0
2. 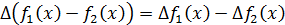
3. 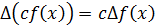
4. 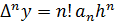
При h 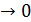 конечные разности первого порядка соответствуют
конечные разности первого порядка соответствуют 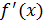 ,
, 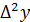 =
= 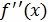 и т.д.
и т.д.
Разделенные разности. В том случае, когда шаг переменный, используем разделенные разности.
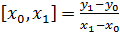
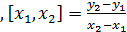 ,
, 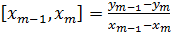 - первый порядок
- первый порядок
k-й порядок: 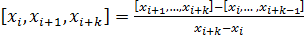
Свойства разделенных разностей эквивалентны свойствам конечных разностей
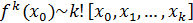
Степень интерполяционного полинома в случае не равно отстоящих узлов выбираются таким образом, чтобы она совпадала с порядком разделенных разностей.
ИП Лагранжа
Пускай дана таблично заданная ф-я f(x), и мы установили, что искомый многочлен дБ степени k. Для построения полинома строится полином след.вида:
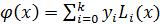 , где
, где 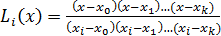 - многочлен Лагранжа
- многочлен Лагранжа
1. Степень i-го полинома влияния=k
2. I-й полином влияния в i-м узле=1.
3. I-й полином влияния во всех остальных узлах=0
В точке λ, которая не совпадает ни с одним узлом, погрешность равна: 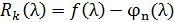 . Если искомая ф-я f(x)-полином, тогда погрешность=0.
. Если искомая ф-я f(x)-полином, тогда погрешность=0.
Теорема: существует единственный полином в степени k, проходящий через (k+1) точку плоскости, удовлетворяющий начальным условиям.
Погрешность можно оценить следующим образом:
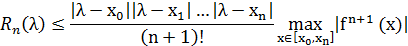
К достоинствам полинома Лагранжа можно отнести тот факт, что коэф-ты полинома зависят только от узлов интерполяции, но в том случае, если добавлен хотя бы 1 узел, то придется пересчитывать все полиномы.
Полином Ньютона.
F(x): 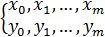
Строится с помощью разделенных разностей.
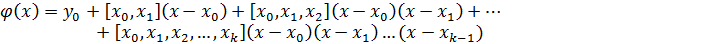
Свойства:
1. Степень 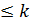
2. В узлах полином совпадает с исходной ф-ей
Положительные стороны:
1. Не требуется вычислять степень полинома. Можно взять 2-ю степень, построить, проверить погрешность, если не удовлетворяет, то повышаем степень до необх точности.
2. При добавлении новой k+1 точки, все найденные ранее коэф-ты сохраняются, а к полиному добавляется:

Сплайн-интерполяция.
f(x) задана на 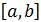 таблично, весь отрезок разбит точками
таблично, весь отрезок разбит точками  .
.
Сплайн порядка n – функция, определенная на 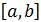 , такая, что на каждом (
, такая, что на каждом ( задана полиномом Sni=
задана полиномом Sni= 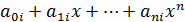
Пусть ф-я Sn на 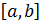 имеет k непрерывных
имеет k непрерывных 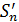 , тогда d=n-k – дефект сплайна.
, тогда d=n-k – дефект сплайна.
Параболическая сплайн-интерполяция
Пусь f(x) задана таблично, S2(x)=S2i(x)= 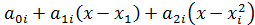
На каждом 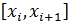
Для построения такого сплайна необходимо найти 3n коэф-та, все они находятся из след условий:
1. Совпадение сплайна на каждом отрезке с заданной ф-ей 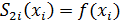
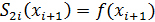
2. Непрерывность первой производной в узлах. Равенство производных соседних полиномов в узле – условие для внутренних узлов.
3. Мы можем задать значение 1-й производной в x0 либо в xn.
Этих условий достаточно, для определение единственного сплайна S2 на отрезке.
Погрешность оценивается след образом:
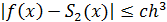 , h=max
, h=max 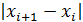
Date: 2015-07-17; view: 774; Нарушение авторских прав