Решение систем линейных уравнений. Метод Гаусса. Контроль точности при решении. Метод простой итерации, условие сходимости

СЛАУ используются для описания дескриптивных моделей.

Т.о. СЛАУ имеет след.вид:

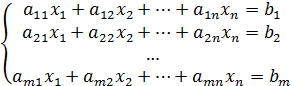AX=B

Метод Гаусса относится к точным методам решения СЛАУ

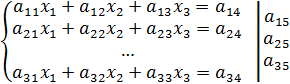∆≠0→решение есть и оно единственное

На первом шаге 1е ур-е делится на 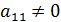, получаем ур-е вида , где b_1j = a_1j/a₁₁, где j=2,3,4. В общем случае на первом шаге получаем n оп.деления

На втором шаге из эл-тов 2го ур-я вычитаем эл-ты первого, умноженные на а₂₁, получаем ур-е a’₂₂x₂+a’₂₃x₃=a’_24. Произведем n операций умножения. Из элементов третьего ур-я вычитаем эл-ты 1го, умнож.на коэф-ты а₃₁. Получаем ур-е a’₃₂x₂+a’₃₃x₃=a’₃₄. Коэф-ты 2го и 3го ур-я вычисляются по формуле:

При этом мы проделываем n² операций умн.и дел. Работаем с полученной системой.

На третьем шаге 2е ур-е делим на а₂₂ 0:

,

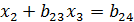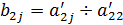
На четвертом шаге: 3е-2е 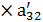, , , j=3,4

На пятом шаге: 3е\

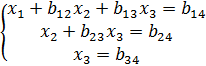- система треугольного вида, где коэф-ты ниже главной диагонали =0.

Эти 5 шагов носят название прямого хода метода Гаусса. Обратный ход заключается в получении значений неизвестных по этой матрице.

Точность метода: применяется метод контрольных сумм для проверки потери точности. Для этого в исх.матрицу добавляется еще один столбец, эл-ты к-го вычисляются по формуле: , где i=1,2,3. При прямом ходе метода Гаусса с эл-ми этого столбца производятся все те же действия, к-е производятся со строками, на любом этапе должно соблюдаться равенство: . После прихода к треугольному виду должны выполняться равенства:

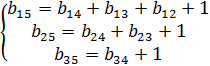
Но контролировать на каждом этапе решения невозможно, поэтому вычисляют дополнительную неизвестную , только в кач-ве столбца своб.членов выступает дополнительный столбец. Получаем систему:

Между основными и дополнительными переменными должно соблюдаться: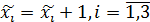

Но реально такого быть не может, поэтому вводится точность 𝛆. Разница между основным и дополнительным x должна удовлетворять следующему: . Если равенство верно, то ответ получен с точностью до 𝛆. Если нет – произошла потеря точности мы попытаемся её восстановить:

1. На 1м шаге обозн как

2. Для каждого ур-я считаем 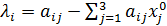- невязка, их подставляем в исх систему в кач-ве столбца своб членов.

3. Решаем новую систему методом Гаусса.

4. Получаем решение 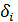- поправки

5. Окончательно имеем результат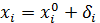

Тем самым для достижения приемлемой точности мы специально идем на потерю времени, решая дважды систему методом Гаусса. Мало того, проверка и восстановление точности может происходить циклически несколько раз.

Метод простой итерации.

МПИ-это приближенный алгоритм решения СЛАУ. Предположим, что исходная система АХ=В каким-либо образом приведена к виду: Х=CX+F, при этом заданы начальные значения искомых переменных. Начальные значения берутся исходя из смысла задачи. Данное нач.зн-е мы подставляем в правую часть системы вида Х=СХ+F. Тем самым получаем новый вектор 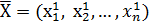. На след.шаге вектор подставляется в правую часть системы , получаем , аналогично делаем до тех пор, пока разность между значениями всех Х_i на каком-то шаге не будет отличаться от значений Х_i на предыдущем (к-1) шаге на величину :

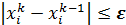
Этот процесс является сходящимся к искомому решению, если выполняется следующее неравенство:

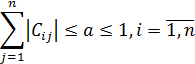
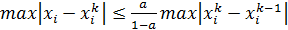- погрешность решения

МПИ явл приближенным методом решения, применяется довольно редко ввиду наличия условия сходимости, сходится довольно быстро, обычно не превышает n итераций, n – кол-во переменных.

Date: 2015-07-17; view: 1036; Нарушение авторских прав