Пример 3.4

П оверхность бесконечно длинного прямого цилиндра радиуса R заряжена однородно поверхностной плотностью 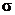. Определите напряженность поля 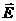и потенциал 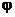внутри и вне поверхности.

Решение.

Сначала определим напряженность электрического поля 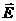. Наличие осевой симметрии в распределении заряда, позволяет сделать вывод о том, что вектор 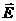в любой точке пространства направлен радиально к оси заряженного цилиндра или от нее, в зависимости от знака заряда. Ввиду той же симметрии величина Е может зависеть только от расстояния до оси:

Е = Е (r)

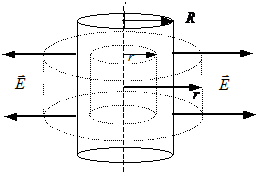
Для определения этой зависимости выберем следующую гауссову поверхность. Построим цилиндр высоты l с боковой поверхностью удаленной от оси на расстояние r и основаниями, перпендикулярными к оси симметрии (рис.5). Поток поля вектора 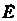через основания цилиндра равен нулю, т.к. 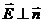. Поток через боковую поверхность равен Е× S, т.к. 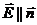, S - площадь боковой поверхности.

Рис.5

Из теоремы Гаусса следует:

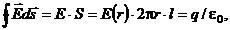
где 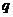- заряд внутри гауссова цилиндра равен:

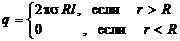
Подставляя поток и заряды в формульное выражение теоремы Гаусса, получим:

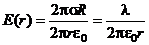,если ;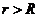

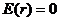, если .

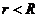Интегрирование напряженности поля, для определения потенциала вне цилиндра, проведем вдоль направления перпендикулярного к оси цилиндра. Выбрав начало отсчета потенциала на поверхности заряженного цилиндра (т.е. 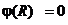при 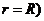получим:

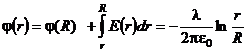
Внутри заряженного цилиндра электрическое поле отсутствует, поэтому потенциал во всех точках имеет одно и тоже значение, равное выбранному значению на его поверхности. Графики электрического поля и потенциала представлены на рис.6 и рис.7 соответственно.

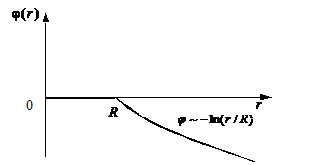
Рис.6	Рис.7

Date: 2015-07-17; view: 330; Нарушение авторских прав