
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Исследование панели сборной железобетонной градирни на транспортныенагрузки
|
|
Целью исследований было определение оптимального расположения опор на транспортном средстве, обеспечивающем трещиностойкость панелей при перевозке.
По данной методике выполнялись исследований с применением методов математического и физического моделирования следующими этапами: экспериментальные исследования на физической модели, выбор и определение неизвестных параметров расчетной модели, проверка адекватности расчетной модели, численные исследования.
Физическое моделирование осуществлялось на модели из упругого материала, так как при транспортировании возникновение трещин в панелях не допускается. Согласно заданной схеме опирания конструкции в процессе перевозки (рис. 5) в ее элементах возникают, в основном, продольные напряжения, что дает возможность при моделировании не учитывать различие коэффициентов Пуассона материалов модели и натуры. С учетом условия подобия запишем:
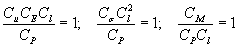
| (8) |
где Си, СЕ, Сl, СР, Сσ, СМ - масштабы соответственно перемещений, модуля упругости, геометрических размеров, нагрузки, напряжений, изгибающих моментов. Поскольку масштабов шесть, а равенств в системе (8) имеем три, то тремя масштабами Сl, СЕ, СР, можем задаваться произвольно.
Исходя из технологических условий принимаем Сl = 0,05. Материал модели - эпоксидная смола ЭД-16М, следовательно, СЕ = 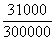 = 0,103. Для удобства нагружения принимаем СР = 0,0032.
= 0,103. Для удобства нагружения принимаем СР = 0,0032.
Подставив принятые, значения Сl, СЕ, СР в систему (8), получим: Си = 0,62; Сσ = 1,28; СМ = 1,6·10-4.
Для изготовления модели применена технология точного литья в размываемые формы.
При экспериментальных исследованиях измерялись прогибы панели в узлах, а также фибровые деформации ребер и поля панели. Значения средних и доверительных оценок результатов прямых измерений прогибов и деформаций определялись по формулам (2).
Определение неизвестных параметров математической модели при транспортировке в горизонтальном положении, когда направление транспортных нагрузок перпендикулярно плоскости панели, выполняется при условии следующих допущений: нагрузка прикладывается в узлах пересечения ребер и воспринимается, в основном, ребрами, так как их жесткость на порядок выше жесткости поля панели. Таким образом, расчетная схема панели представляется в виде стержневой системы, у которой оси стержней совпадают с физическими осями ребер (см. рис. 5). Часть исходных данных известна (координаты узлов, нагрузка). Не известны жесткостные характеристики приведенного сечения ребер.

Рис. 5. Горная панель градирни а - общий вид; б - расчетная схема
Для их определения необходимо выявить расчетную ширину полки таврового сечения. В такой постановке задача решалась экспериментально-теоретически с использованием данных тензометрических измерений фибровых деформаций. При этом, если расчетную ширину полки принять за х, то, исходя из гипотезы плоских сечений, получим:
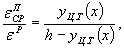
| (9) |
где 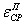 - усредненная по всей ширине х деформация в полке;
- усредненная по всей ширине х деформация в полке; 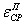 =
= 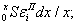 εР - фибровая деформация ребра; уЦ.Т(х) - расстояние центра тяжести сечения с шириной полки х до верха плиты.
εР - фибровая деформация ребра; уЦ.Т(х) - расстояние центра тяжести сечения с шириной полки х до верха плиты.
Решение уравнения (9) получено методом последовательных приближений. Расчетная ширина полки х. определялась для опорных и пролетных сечений ребер.
Проверка адекватности расчетной модели выполнялась сравнением критериев Т и R вычисляемых по формулам (27) и (28) методических рекомендации соответственно. Для этого сначала находили средние значения и доверительные интервалы экспериментальных и теоретических величин сравниваемых параметров соответственно. Для прогибов оценка средних и доверительных значений выполнялась по формуле (2). Для изгибающих моментов аналогичные оценки выполнялись по формулам (8) и (9) с учетом равенства (таблица).
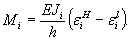
| Параметры НДС | Значения | R | Т | Оценка адекватности (+) или неадекватности (-) расчетной модели | |||
| теоретические | экспериментальные | ||||||
| Средние | Доверительный интервал | Средние | Доверительный интервал | ||||
| Прогибы, мм | |||||||
| у1 | 87,1, | 18,6 | 84,3 | 1,6 | 2,8 | 18,7 | + |
| у2 | 12,4 | 7,9 | 19,4 | 0,9 | + | ||
| у3 | -16,7. | 10,9 | -0,1 | 1;3 | 16,6 | 11,3 | - |
| у4 | 85,2 | 20,6 | 88,6 | 0,9 | 3,4 | 20,6 | + |
| У5 | -12,5 | 9,7 | 0,8 | 0,6 | 13,2 | 9,8 | - |
| Изгибающие моменты, Н·см | |||||||
| М3 | 10,1 | 3,4 | 9,6 | 2,4 | 0,5 | 5,6 | + |
| М7 | -34,5 | 2,8. | -31,4 | 3,1 | 7,9 | + | |
| М8 | -2,2 | 4,6 | 2,4 | 0,9 | 4,6 | 4,7 | + |
Доверительные интервалы теоретических значений параметров получены с применением математической теории планирования экспериментов по формулам (11), (12) и (26) настоящих методических рекомендаций на основании численного эксперимента. При этом учитывалась изменчивость следующих факторов:
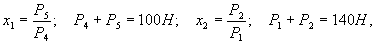
х3 - расстояние от торца панели силы Р4; х5 - то же, Р1; х4 - расстояние от оси опоры силы Р5; х6 -то же, Р2; х7 - расстояние опоры от оси панели.
При учете влияния семи факторов численные эксперименты проводились в соответствии с матрицей планирования 3 < n ≤ 7 (см. приложение 1). Значения факторов в центре плана и их доверительные интервалы были соответственно 1,5 ±0,15; 2,23 ±0,33; 6 ±3 мм; 42 ±4 мм; 6 ±3; 21 ±4 мм; 102 ±2 мм. Полученные средние значения и доверительные интервалы параметров напряженно-деформированного состояния: прогибов в точках 1...5 и изгибающих моментов в точках 3...8 - приведены в таблице совместно с результатами вычислений проверки адекватности расчетной модели.
Из таблицы видно, что почти по всем параметрам расчетная модель адекватна физической. В точках неадекватности теоретические значения превышают экспериментальные, кроме того, значения параметров НДС в точках неадекватности гораздо ниже экстремальных показателей. Исходя из этого, а также цели проводимых исследований, делаем вывод о пригодности математической модели для дальнейших численных исследований.
Численные исследования проводились для определения оптимального расположения опор при транспортировании панелей. Критерием оптимальности было условие удовлетворения равнопрочности по трещиностойкости опорных и пролетных сечений. Для натурной конструкции после ряда преобразований оно запишется как:
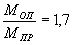
где МОП - изгибающий момент в продольном ребре у опоры; МПР - то же, в пролете.
Выполнив серию расчетов, в которых варьировалось расстояние опор от середины продольных ребер, находим их оптимальные значения: 2180 мм по одному продольному ребру и 2340 - по другому. При этом обеспечивается трещиностойкость панели в процессе перевозки.
литература
1.Клиланд Д., Кинг В. Системный анализ и целевое управление. -М.; Советское радио, 1974.- 278 с.
2. Садовский В.И. Основания общей теории систем. - М.: Наука, 1974. - 215 с.
3.Блауберг И.В., Юдин Э.Г, Становление и сущность системного подхода. - М.; Наука, 1973. - 270 с.
4. Шаханович Ю.А. Введение в современную математику. - М.: Наука, 1965. - 376 с.
5. Мальцев А.И. Алгоритмы и рекурсивные функции. - М.: Наука, 1965. - 391 с.
6. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. - М.: Наука, 1974. - 224 с.
7.Эйкхофф П. Основы идентификации систем управления. - М.: Мир, 1975. - 683 с.
8. Дыховичный А.А., Вишневецкий А.И. Экспериментальные исследования упругих систем и математическое моделирование. - В кн.: Сопротивление материалов и теория сооружений. - Киев: БудIвельник, 1980, вып.36,.с.107-110.
9. Duhovichnuj A.A. Matematikal Modellezes a szerkezet-kutatasban. - Epitest Kutatas Feilesztes. 1982, № 4, p.209-211.
10. Безухов Н.И., Лужин О.В. Приложение методов теории упругости и пластичности к решению инженерных задач. - М.: Высшая школа, 1974.
11.Аргирос Дж. Энергетические теоремы и расчет конструкций. В кн.: Современные методы расчета сложных статически неопределимых систем. - Л: Судпромгиз., 1961.
12. Washizu K. Variational Method in Elasticity and Plasticity. PergamonPress, Oxford – Braunchweig, 1966
13.Сливкер В.И. Об одной смешанной вариационной постановке задач для упругих тел. - Механика твердого тела, 1982, №4, с. 88-97.
14. Образцов И.Ф. Вариационные методы расчета тонкостенных авиационных пространственных конструкций. - М.: Машиностроение, 1966.
15.Розин Л.А. О связи метода конечных элементов с методами Бубнова-Галеркина и Ритца. - В кн.: Строительная механика сооружений. Л.: Изд-во ЛПИ, 1971.
16. Зенкевич O.K. Метод конечных элементов в технике. - М.: Мир, 1975.
17. Розин Л.А. Метод конечных элементов в применении к упругим системам. - М.: Стройиздат, 1977.
18.Постнов В.А., Хархурим И.Я. Метод конечных элементов в расчетах судовых конструкций. - Л.: Судостроение, 1974.
19. Немчинов Ю.И. Расчет пространственных конструкций (метод конечных элементов). - К.: БудIвельник, 1980.
20.Пустыльник Е.И. Статистические методы анализа и обработки наблюдений.- М.: Наука, 1968. - 288 с.
21.Линник Ю.В. Метод наименьших квадратов и основы математико-статистической теории обработки наблюдений.- М.: Физматгиз, 1962. - 352 с.
22.ГОСТ 8.207-76. Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений.
23. Адлер Ю.П. Введение в планирование эксперимента. - М.: Металлургия, 1969. - 279 с.
24. Налимов В.В., Чернова Н.А. Статистические методы планирования экстремальных экспериментов. - М.: Наука, 1966.
25. Шторм Р. Теория вероятностей, математическая статистика, статистический контроль качества. М.: Мир, 1979. - 368 с.
26. Harrington E.C. Indust. Quality Control, 1965, 21, № 10.
27. КирпичёвМ.В. Теорияподобия. -М.:Изд. АН СССР, 1953. - 93 с.
28. Седов Л.И. Методы подобия и размерности в механике. - М.: Наука, 1972.
29. Назаров А.Г. О механическом подобии твердых деформируемых тел. - Ереван: Изд. АН АрмССР, 1965.
30. Вентцель Е.С. Теория вероятностей. - М.: Наука, 1964. -576 с.
31. Городецкий А.А., Здоренко B.C. Расчет физически нелинейных плоских рамных систем. - В сб.: ЭВМ в исследованиях и проектировании объектов строительства, вып. I. - К.: БудIвельник, 1970.
32. Бондаренко В.М., Бондаренко С.В. Инженерные методы нелинейной теории железобетона. - М.: Стройиздат, 1982.
33. Гениев Г.А., Киссюк В.Н., Тюпин Г.А. Теория пластичности бетона и железобетона. - М.: Стройиздат, 1974
34. Ильюшин А.А. Пластичность. - М.: Гостехиздат, 1948.
35. Лехницкий С.Г. Теория упругости анизотропного тела. - М.: Наука, 1977.
36.Фудзии Т., Дзако М. Механика разрушения композиционных материалов. - М.: Мир, 1982.
37.Постнов В.А., Дмитриев С.А., Елтышев Б.К., Родионов А.А. Метод суперэлементов в расчетах инженерных сооружений. - Л.: Судостроение,1979.
38. Кретов В.И., Вишневецкий А.И. О получении матрицы жесткости суперэлемента. - Строительная механика и расчет сооружений, 1983, № 5
Date: 2015-07-17; view: 612; Нарушение авторских прав