
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Физическое моделирование
|
|
1.4.1. Физическое моделирование (физический эксперимент) представляется важной частью исследований, несмотря на то, что это наиболее ресурсоёмкий процесс, требующий участия большого количества исполнителей различных специальностей и квалификации. В целях ускорения и повышения эффективности таких исследований с позиции системного подхода объем его должен быть необходимым и достаточным для решения задач:
определения и уточнения неизвестных параметров расчетных моделей;
проверки адекватности расчетной модели (устанавливается критерий оценки ее достоверности и точности).
Таблица 1
| Наименование программы | Назначение | Метод, возможности программы | Организация-разработчик |
| ППП АПЖБК (ЛИРА) | Расчет пространственных систем | МКЭ, стержни, плиты, пластины статика, динамика, сейсмика, нелинейность, РСУ, подбор арматуры | НИИАСС Госстроя УССР (Киев) |
| ПРОКРУСТ | То же | То же, суперэлементы | ДонецкийПромстройНИИпроект Госстроя УССР |
| МАРСС-ЕС | Расчет пространственных стержневых систем | МКЭ, статика, динамика сейсмика, подбор арматуры | ЦНИИпроект Госстроя СССР, (Москва) |
| ПРОЧНОСТЬ | Расчет пространственных систем | МКЭ, библиотека, КЭ, ста тика, динамика, нелинейность | КИСИ (Киев), Минвуз УССР |
| ИКАРУС, ФЕНИКС | Расчет плоских и пространственных пластинчатых систем | МКЭ, пластины, нелинейность | Кишиневгорпроект (Горисполком) |
| КАПРИЗ | Расчет плит с учетом трещин | МКЭ, нелинейность, статика | Киев, ЗНИИЭП (Госгражданстрой) |
| СПРИНТ | Расчет конструкций зданий и сооружений | МКЭ, плоские и пространственные КЭ, статика, динамика, сейсмика, температура, нелинейность | МИИТ (Москва), Минвуз СССР |
| КОНТУР | Расчет зданий и сооружений как простран- | Метод пространственных КЭ, упругие связи, нелинейность материала и основания, статика, динамика, сейсмика | НИИСК Госстроя СССР, (Киев) |
| ТОСТ | Расчет зданий с несущими стенами | Составные тонкостенные стержни, статика, динамика, сейсмика, упругое основание | Киевпроект, (Горисполком) |
1.4.2. Физической моделью считается материальная система, свойства и параметры которой подобны реальному объекту, с контролируемыми входными и выходными параметрами, оснащенная необходимыми измерительными приборами и нагружающими устройствами. В качестве таковой может быть использован и сам объект исследований, если он подготовлен соответствующим образом к испытаниям.
1.4.3. Физическое моделирование включает:
разработку методики экспериментальных исследований, рабочих чертежей модели и приспособлений для ее испытаний;
изготовление и монтаж модели и приспособлений для испытаний;
подготовку модели к испытаниям, оснащение ее приборами и тензометрическими датчиками;
испытание модели в соответствии с методикой исследований;
обработку результатов эксперимента (не являясь окончательной целью исследований, они служат исходными данными для построения и проверки адекватности математических моделей объекта исследований).
1.4.4. Особые требования к эксперименту следует предъявлять при системном подходе к исследованиям сложных строительных конструкций с использованием прямой и обратной связи между физическим и математическим моделированием. Однако ввиду того, что результат даже наиболее тщательно подготовленного эксперимента носит случайный характер, каждый раз в обязательном порядке необходимо завершать процесс анализом и оценкой степени риска от той или иной ошибки в полученных результатах с применением методов математической статистики. Если величина ошибки или риска настораживает, рекомендуется идти по пути ее уменьшения применением более точной методики наблюдений, устранением наиболее значительных помех и т.д.
1.4.5. Наибольшие погрешности в результатах эксперимента (систематические, грубые и случайные) связаны с:
неоднородностью физико-механических и неточностью геометрических характеристик объекта исследований;
несовершенством устройств, создающих необходимое воздействие на объект;
изменением внешних условий;
погрешностью измерительного комплекса.
1.4.6. Систематическими по п. 1.4.5 считаются ошибки, повторяющиеся и одинаковые по всей серии наблюдений, проводимых единым методом с помощью одних и тех же измерительных приборов. Основная их особенность - то, что они входят в общую ошибку измерений, благодаря чему возможно в значительной степени их исключение с введением соответствующей поправки.
Один из способов уменьшения систематической ошибки - калибровка измерительных приборов до начала эксперимента. Для определения систематической ошибки измерительного комплекса во время эксперимента рекомендуется параллельно с измерением физических величин на исследуемом объекте устанавливать аналогичные величины тем же измерительным комплексом на объекте-эталоне, дающем возможность выполнять измерения другим методом, точность которого превышает точность метода, используемого в эксперименте.
1.4.7. Грубые ошибки по п. 1.4.5 настоящих методических рекомендаций вызываются резким изменением (флуктуацией) во время испытаний внешних условий, невнимательностью экспериментатора и пр. В отличие от систематической ошибки, характеризуемой неизменностью во всей серии испытаний, грубая присутствует не более чем в одном-двух испытаниях и характеризуется резким отличием по абсолютной величине от рядовых ошибок измерений.
Учесть ее заранее невозможно, поэтому необходимо повышать уровень подготовки и проведения испытаний. Если, вопреки тщательности эксперимента, появляются сомнения в каком-либо показателе, его отбрасывают. Во всех сомнительных случаях используются специальные статистические критерии, позволяющие объективно выделять в каждой серии измерений имеющиеся грубые ошибки [20].
1.4.8. Случайные ошибки (cм. п. 1.4.5) различны по величине и непредсказуемы даже при измерениях, выполняемых одинаковым способом. Однако их распределение симметрично относительно нуля, т.е. при отсутствии систематических и грубых ошибок истинный результат измерений является математическим ожиданием соответствующей случайной величины.
В соответствии с ГОСТ 8.207-76[22] результаты прямых измерений параметров должны быть представлены в форме:
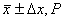 , ,
| (1) |
где 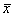 - результат измерений (математическое ожидание); Δx - доверительные границы измеренной величины; Р - доверительная вероятность (надежность выполненных измерений), обычно в экспериментах принимаемая равной 0,9 и 0,95.
- результат измерений (математическое ожидание); Δx - доверительные границы измеренной величины; Р - доверительная вероятность (надежность выполненных измерений), обычно в экспериментах принимаемая равной 0,9 и 0,95.
1.4.9. В подавляющем большинстве реальных испытаний при количестве повторяемых наблюдений n < 15 случайные ошибки измерений по п. 1.4.8 распределяются по нормальному закону. В этом случае характеристики измеренной величины, приведенные в (1), вычисляются по формулам:
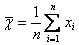 ; ;
| |
 , ,
| (2) |
где n - число результатов наблюдений одной величины; xi - i -тый результат наблюдения; t(p.f) - коэффициент Стьюдента, в зависимости от доверительной вероятности Р и числа степеней свободы f = n - 1, определяемый по таблицам t -распределения; S (х) - среднее квадратическое отклонение результата измерений, оцениваемое по формуле:
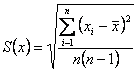 , ,
| (3) |
1.4.10. Статистическая обработка результатов измерений по пп. 1.4.8 и 1.4.9 используется при оценке одной величины (например, физико-механических характеристик материалов конструкций). В процессе же экспериментальных исследований строительных конструкций проводятся измерения большой группы однородных величин, хотя не всегда имеется возможность повторять измерения по 6 - 10 раз. В случае допущения о равной точности приборов одного типа можно получить достаточно достоверные доверительные интервалы Δх, используя при обработке результаты всех наблюдений. При этом число повторных наблюдений может быть сокращено не менее чем до двух.
Пусть выполнены измерения группы из т однородных величин и повторены п раз. Для каждой величины вычисляются выборочные средние значения и выборочные дисперсии:
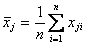 ;
;
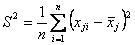 , ,
| (4) |
Так как дисперсии равноточных измерений одинаковы, средняя квадратическая ошибка S(x) будет одинакова для всех 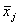 :
:
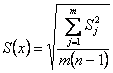 , ,
| (5) |
а доверительный интервал Δx может быть установлен по формуле (2) с определением коэффициента Стьюдента при числа степеней свободы f = n - 1.
1.4.11. В случае принятия в качестве результата экспериментальных исследований таких физико-механических характеристик объекта u = f (x1, x2,..), которые получаются в результате математических действий с несколькими случайными величинами xt, каждая из которых измерена непосредственно с доверительными интервалами Δxt при одинаковой доверительной вероятности Р, доверительный интервал функции оценивается по формуле:
 , ,
| (6) |
(t = 1, 2, …., k).
Date: 2015-07-17; view: 727; Нарушение авторских прав