Экспоненциальный закон

Прежде всего, следует отметить, что экспоненциальное распределение характерно для внезапных отказов элементов и систем в целом. Экспоненциальное распределение хорошо описывает время безотказной работы сложных систем, состоящих из большого числа разнородных компонентов, а также электронной аппаратуры. Кроме того, вследствие неизменности величины интенсивности отказов расчеты надежности при применении этого распределения наиболее просты. В этом случае функция распределения наработки до отказа представлены в общем виде на рис. 4.2, а.

Функция плотности вероятности времени безотказной работы имеет вид:

при t_i ³ 0. (1)

Оценка параметра l производится по формуле:

.

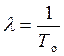Нормальный закон (рис. 4.2, б)

Нормальный закон наиболее часто используется для оценки надежности изделий при наличии постепенных отказов. Нормальное распределение используется для описания систем и элементов, подверженных действию износа. Плотность вероятности нормального закона задается отношением:

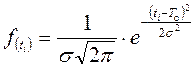при t_i ³ 0 (2)

где Т _о - средняя наработка до отказа;

s - среднее квадратическое отклонение.

Оценка параметров Т _о и s для всех планов испытаний производится по формулам:

,

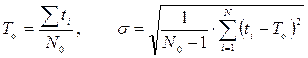где t_i - моменты отказов оборудования или машин (табл. 4.4);

N - число наблюдений.

Формулы для расчета показателей надежности при нормальном распределении, с учетом функции Лапласа, приведены в табл. 4.4. Графики распределения представлены на рис. 4.2, а.

Это распределение описывает поведение случайных величин в интервале (- ∞, + ∞). Однако время является неотрицательной величиной. Поэтому также используется усеченное нормальное распределение, при t >0. При этом вероятность безотказной работы, плотность распределения наработки до отказа, частота отказов и наработка до отказа определяются по соотношениям, приведенным в табл. 4.4.

Date: 2015-07-17; view: 748; Нарушение авторских прав