
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Указания к выполнению задачи №2
|
|
Таблица №2
| № вари- анта | l,см | d,см | в,см | I,мА | V,В | В,Тс | VX, В |
| 0,2 | 0,2 | 0,25 | 0,6 | +0,056 | |||
| 1,2 | 0,3 | 0,3 | 0,4 | 1,2 | -0,12 | ||
| 0,8 | 0,2 | 0,3 | 0,35 | 0,8 | +0,04 | ||
| 0,3 | 0,2 | 0,3 | 0,5 | +0, 03 | |||
| 0,6 | 0,2 | 0,4 | 0,5 | -0,15 | |||
| 0,7 | 0,3 | 0,4 | 0,45 | 0,4 | -0,02 | ||
| 1,1 | 0,4 | 0,4 | 0,6 | 0,7 | +0,2 | ||
| 0,6 | 0,3 | 0,3 | 0,7 | +0,15 | |||
| 0,9 | 0,2 | 0,2 | 0,8 | -0,22 | |||
| 0,8 | 0,2 | 0,4 | 0,5 | 0,8 | -0,035 |
Формулы и выражения, которыми можно воспользоваться при выполнении задачи №2:
Если полупроводник, по которому течет электрический ток I, поместить в магнитное поле индукцией В, то возникает поперечная ЭДС Холла:
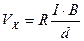 ,
,
где постоянная Холла 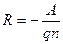 для полупроводника п – типа проводимости и
для полупроводника п – типа проводимости и 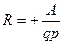 для дырочного полупроводника., здесь п и р – концентрации носителей тока, А постоянная, определяемая типом рассеяния носителей тока и для атомных полупроводников (Si, Ge, GaAs) А = 1,18. Холловская подвижность выражается формулой
для дырочного полупроводника., здесь п и р – концентрации носителей тока, А постоянная, определяемая типом рассеяния носителей тока и для атомных полупроводников (Si, Ge, GaAs) А = 1,18. Холловская подвижность выражается формулой 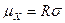 , где
, где 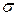 - электропроводность полупроводника. Постоянная А может быть также определена формулой
- электропроводность полупроводника. Постоянная А может быть также определена формулой 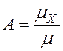 , где
, где 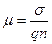 обычная подвижность. Расчет коэффициента диффузии
обычная подвижность. Расчет коэффициента диффузии 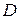 проводится на основе формулы Эйнштейна
проводится на основе формулы Эйнштейна 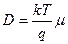 .
.
Date: 2015-06-11; view: 458; Нарушение авторских прав