Вращающийся Aвектор, равный сумме векторов A1 иA2 , изображающих соответственногармонические колебания1 - го грузикаотносительно 2- го грузикаи гармонические колебания 3 page

При Ω →∞ получим в установившемся состоянии из (2.62) амплитуду A_в→0 и

tgφ₀→ 0, а φ₀ → π.

Механический резонанс колебательных процессов

Амплитуда (2.62) A_в смещения z(t) (рис. 02.0.14) тела m массой, совершающего на пружине вынужденные гармонические колебания относительно статического удлинения пружинного маятника, т.е. относительно O' начала координат, в зависимости от t времени, достигает максимума при Ω_р циклической резонансной частоте гармонических колебаний вектора F_в = k F₀ cosΩ_рt внешней периодической силы. Эта Ω_р циклическая резонансная частота гармонических колебаний связана с ω₀ циклической (2.2 ) частотой гармонических колебаний пружинного маятника и его (2.47)

β коэффициентом затухания следующим выражением: Ω_р = (ω₀ ²- 2β²)^1/2 = (ω ²- β²)^1/2, (2.63) где ω - циклическая частота свободных затухающих колебаний маятника.

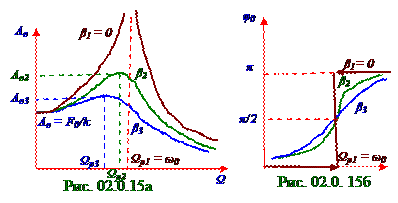
На амплитудной характеристике (рис. 02.0.15а) вынужденных гармонических колебаний с увеличением β коэффициента, т.е. β₃ > β₂ > β₁, циклическая Ω_р резонансная частота уменьшается, т.е. Ω_р3 < Ω_р2< Ω_р1, c одновременным уменьшением A_в резонансной амплитуды колебаний,т.е.

A_в3 < A_в2< A_в1. Если Ω циклическая частота гармонических колебаний вектора F_в = k F₀ cosΩ_рt внешней периодической силы равна нулю, т.е. Ω = 0, то амплитуда A_в смещения z(t) (рис. 02.0.14) тела

m массой равна F₀/mω₀², т.е. маятник не колеблется, а имеет статическое смешение из положения равновесия под действием вектора F_в = k F₀ постоянной во t времени силы.

При (рис. 02.0.15а) равенстве β₁ коэффициента затухания нулю, т.е. при β₁ = 0, и равенстве

Ω_р циклической частотыгармонических колебаний вектора F_в = i F₀ cosΩ_рt внешней периодической силы циклической ω₀ (2.2) частоте гармонических колебаний у пружинного маятника наступает резонанс, при котором (2.62) A_в амплитуда установившихся вынужденных колебаний (рис. 02.0.15а) стремится к бесконечности, т.е. A_в→ ∞.

При конечном значении β коэффициента затухания резонансная A_вр амплитуда колебаний или максимальная амплитуда, которая получается при подстановке (2.63) Ω_р циклической резонансной частоты гармонических колебаний вектора F_в = k F₀ cosΩ_рt внешней периодической силы в (2.62) выражение, имеет следующий вид: A_вр = F₀/2mβω = πF₀/mδω², (2.64)

где использованы выражения (2.54) δ = βT - логарифмического декремента затухания и (2.50)

T = 2π/ω - периода T свободных затухающих колебаний.

На рис. 02.0.15б изображена фазо - частотная характеристика установившихся вынужденных гармонических колебаний маятника.

При равенстве Ω циклической частоты гармонических колебаний вектора внешней периодической силы F_в = k F₀cosΩt циклической ω₀ частоте гармонических колебаний отставание

относительно положения равновесия равно нулю.

При Ω < ω₀ смещение и периодическая сила находятся в фазе, т.е. направления вектора силы и вектора смещения колеблющейся системы совпадают. При Ω > ω₀ смещение и периодическая сила находятся в противофазе, т.е. направления вектора силы и вектора смещения колеблющейся системынаправленыв противоположные стороны.

Лекция 6. Виды механических волн. Основы акустики. Элементы физиологической акустики. Уравнение синусоидальной бегущей плоской и сферической волн, длина волны, фазовая скорость. Звуковые волны в газах. Волновое уравнение распространения акустических волн в линейной однородной изотропной непоглощающей упругой среде: фазовая скорость распространения звука. Волновое уравнение, фазовая скорость распространения продольных упругих волн в стержнях. Волновое уравнение, фазовая скорость распространения поперечных волн в гибком шнуре. Давление звука, интенсивность звуковой волны. Объемная плотность энергии упругих волн. Вектор Умова - вектор плотности потока энергии упругих волн. Когерентные волны в упругой среде. Интерференция этих волн. Стоячая волна в непоглощающей упругой среде: уравнение смещений частиц упругой среды относительно положений равновесия; расчёт координат узлов и пучностей; уравнения скорости смещений и относительной деформации частиц упругой среды относительно положений равновесия

Виды механических волн. Основы акустики. Элементы физиологической акустики.

Упругой волной называютназывают процесс распространения возмущения в упругой среде. При этом происходит распространение именно возмущения частиц среды, но сами частицы испытывают движение около своих положений равновесия. Среда, в которой распространяется упругая волна, представляется сплошной и непрерывной без учёта её дискретного или молекулярного строения.

Упругая волна называется продольной, если частицы среды колеблются в направлении распространения волны. Продольные волны связаны с объемной деформацией упругой среды и потому могут распространяться в любой среде - твердой, жидкой и газообразной, например - звук в воздухе. Упругая волна называется поперечной, если частицы среды колеблются, оставаясь в плоскостях, перпендикулярных к направлению распространения волн. Поперечные волны связаны с деформацией сдвига упругой среды и могут образовываться и распространяться только в средах, обладающих упругостью, т.е. в твердых телах. Поперечная волна - колебание струн музыкальных инструментов.

Особое место занимают поверхностные волны, распространяющиеся вдоль свободной поверхности жидкости или поверхности раздела двух несмешивающихся жидкостей. В образовании и распространении этих волн определяющую роль играют силы поверхностного натяжения и тяжести. При изменении объёма газа, вызываемое внешними воздействиями, вследствие упругих свойств этого газа происходит изменение его давления. Упругими свойствами обладают твёрдые, жидкие и газообразные тела. Упругими деформациями тел называют такие, которые после исчезновения внешних воздействий полностью восстанавливают свою первоначальную форму. Для упругих деформаций газов справедлив закон Гука, согласно которому элементарное dp приращение давления газа при малом изменении dV его объема прямо пропорционально относительной dV/V объемной деформации, вследствие чего имеет место следующее выражение: dp = - kdV/V, (2.65)

где k - модуль объемной упругости газа. Знак "-" в (2.65) указывает на то, что при положительном dp приращении давления газа dV приращение объема отрицательно и наоборот. При очень медленном изменении объема газа процесс можно считать изотермическим, а при очень быстром - адиабатическим. В первом случае модуль объемной упругости газа имеет значение: k = p, т.е равен в произвольный момент времени давлению газа, а во втором случае модуль объемной упругости газа имеет значение: k = γp, где γ - показатель адиабаты газа.

Звуковыми или акустическими волнами называются упругие волны малой интенсивности, т.е. слабые механические возмущения, распространяющиеся в упругой среде. Звуковые волны, воздействуя на органы слуха человека, способны вызвать звуковые ощущения, т.е. слышимые звуки, если ν частоты соответствующих им колебаний лежат в пределах 16 - 2·10 ⁴ Гц. Упругие волны с частотами ν < 16 Гц называются инфразвуком, а с частотами ν > 2·10 ⁴ Гц - ультразвуком. Часто упругие волны с частотами ν > 10 ⁹ Гц называют гиперзвуком. Распространение упругих волн в среде не связано с переносом вещества. В неограниченной среде оно состоит в вовлечении в вынужденные колебания все более и более удаленных от источника волн частей среды. Некоторый перенос вещества может осуществляться при распространении в среде сильных возмущений, например, ударных волн, возникающих при взрыве, когда колебания частиц среды становятся нелинейными.

Среда называется однородной, если её физические свойства при неизменных условиях и существенных в рассматриваемых задачах, не изменяются от точки к точке. Среда называется изотропной, если её физические свойства, существенные в рассматриваемых задачах, одинаковы во всех направлениях. Среда называется линейной, если между величинами, характеризующими рассматриваемое внешнее воздействие на среду, существует прямо пропорциональная связь. Например, упругая среда, подчиняющаяся закону Гука, линейна по своим механическим свойствам. Бегущими волнами называются волны, которые в отличие от стоячих волн, переносят энергию в пространстве.

Уравнение синусоидальной бегущей плоской и сферической волн, длина волны, фазовая скорость.

Механические возмущения или деформации распространяются в упругой среде с конечной v скоростью. Поэтому возмущение, вызываемое источником волны в начальный момент t₀ времени и приводящее к смещению частиц упругой среды на максимальное A отклонение от положения равновесия достигает с запаздыванием на промежуток τ время M точек пространства, расположенных в плоскости равных фаз и находящихся от начала координат на y расстоянии. Плоскостью равных фаз или волновой поверхностью или фронтом волны называется геометрическое место точек, в которых фаза колебаний имеет одно и то же значение. Волновая поверхность отделяет возмущённую область упругой среды, в которой частицы этой среды вовлечены в волновой процесс, от невозмущённой области, в которой частицы упругой среды находятся в равновесном состоянии. Волна называется плоской, если её волновые поверхности представляют совокупность плоскостей, параллельных друг другу. В плоской волне, распространяющейся вдоль OY оси, все s величины, характеризующие смещение точек среды относительно положения равновесия в процессе колебательного движения, зависят от t времени и y координаты рассматриваемой точки среды.

На рис. 02.0. 16 в начальный момент t₀ = 0 времени И источник, находящийся в плоскости, проходящей через OO начало координат, создаёт в упругой среде плоский волновой фронт, т.е. все частицы, находящиеся в Пл. 1 плоскости равных фаз имеют одинаковые отклонения относительно положения равновесия, равные A амплитуде колебаний.

Если И источник создаёт гармонические колебания в Пл. 1 плоскости равных фаз, которая в момент t₀ = 0 временинаходится в начале OO координат, то зависимость s=s(t) отклонения колеблющихся частицот положения равновесия в Пл. 1 плоскости равных фаз произвольный момент t времени подчиняется (2.28) уравнению: s =A cos(ωt+ φ₀), где ω – циклическая частота гармонических

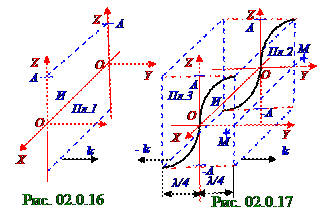
волнового фронта,в OO начале координат частицы упругой среды согласно (2.8) уравнению будут находиться в положении равновесия, т.е. s отклонения колеблющихся частицот положения равновесия будут равны 0. По упругой среде в положительном (рис. 02.0.17)направлении OY оси к моменту t₁ = T/4 времени A максимальное отклонение частиц от положения равновесия дойдёт в направлении k волнового вектора, направленного в положительную сторону OY оси, с фазовой

v скоростью до Пл. 2 плоскости, проходящей через MM прямую и отстоящей от OO начала координат на y₁ = λ/4 расстоянии, где λ - длина плоской бегущей волны. Отклонение s₁ от положения равновесия в Пл. 2 плоскости, проходящей через MM прямую, с учетом τ = T/4 временного запаздывания, за которое плоская бегущая волна распространяется от И источника до этой

Пл. 2 плоскости, согласно (2.66) имеет следующее значение:

s₁ = Acosω(t₁ - τ) = A cosω(t₁ - T/4) = A, (2.67) где t₁ = T/4 - момент времени, отсчитанное от начального t₀ = 0 времени. Ещё через три четверти 3T/4 периода колебаний И источника плоского волнового фронта, т.е. к моменту t₂ = T времени, максимальное A отклонение частиц от положения равновесия дойдёт в направлении k волнового вектора, направленного в положительную сторону OY оси, с фазовой v скоростью до Пл. 2 плоскости, отстоящей от OO начала координат на расстоянии y₂ = λ. При этом И источник плоского волнового фронта вернётся в первоначальное состояние, в котором он находился в момент t₀ = 0 времени, т.е совершит один период T своих колебаний. Таким образом, плоский волновой фронт или плоская волна, находящаяся в начальный момент t₀ = 0 времени (рис. 02.0.16), (рис. 02.0.17) в Пл. 1 плоскости, за Δt = T промежуток времени распространитсяна расстояние, равное λ длине волны. Согласно (рис. 02.0.2) представлению колебаний векторными диаграммами одному периоду T гармонических колебаний И источника (рис. 02.0.16) плоской волны соответствует поворот вектора A с модулём, равным амплитуде гармонических колебаний этого

И источника плоской волны, на 2π угол. За время T периода гармонических колебаний И источника плоская волна распространитсяв упругой среде на расстояние от этого И источника, равное λ длине плоской волны. За время распространения плоской волны на λ расстояние И источник гармонических колебаний изменит фазу своих колебаний на угол 2π. Поэтому частицы упругой среды, имеющие расстояние между собой, равное λ длине волны, имеют различие по фазе колебаний этих частиц, равное 2π. Фазовая v скорость волны численно равна расстоянию, на которое перемещается Пл плоскость равных фаз этой волны за единицу времени, вследствие чего выражение для определения фазовой v скорости имеет следующий вид:v = λ/T. (2.68) где λ - расстояние, численно равное длине волны, которое плоская волна преодолевает с фазовой v скоростью за промежуток времени, численно равный T периоду гармонических колебаний И источника этой плоской волной.

В произвольный момент t времени плоская волна будет находиться на y расстоянии от начала координат, в которое придет с τ = y/ v временным запаздыванием, где v - фазовая скорость перемещения (2.68) в (рис. 02.0.17) направлении k волнового вектора, перпендикулярного Пл. 2 плоскому волновому фронту и направленного в положительную сторону OY оси. Вследствие этого

s=s(t) отклонение от положения равновесия частиц упругой среды в произвольный момент t времени, т.е. уравнение распространяющейся в положительную сторону OY оси плоской синусоидальной волны, с учетом (2.67) имеет следующий вид:

s = A cos[ω(t - τ)+ φ₀] = A cos[ω(t - y/ v )+ φ₀] = Acos[ωt - (ωy/ v ) + φ₀] = Acos(ωt - ky + φ₀), (2.69) где y - координата упругой среды, в которой определяется s=s(t) отклонение; φ₀ - начальная (2.8) фаза колебаний частиц упругой среды в Пл. 1 плоскости с y = 0 координатой, т.е. в Пл. 1 плоскости равных фаз, где находится (рис.2.16) И источник гармонических колебаний, в начальный момент

t₀ = 0 времени; k = ω/ v - волновое число, равное модулю k волнового k вектора, перпендикулярного (рис. 02.0.17) плоскому Пл. 2 волновому фронту и направленного в положительную сторону OY оси в упругой среде.

С учетом выражения ω = 2πν = 2π/T циклической или круговой частоты периодических колебаний из параграфа " Кинематика гармонических колебаний ", где ν - частота гармонических колебаний, создаваемых И источником (рис. 02.0.16) в упругой среде, волновое k число (2.69) принимает следующий вид: k = ω/ v = 2π/ v T = 2π/λ. (2.70) где λ = v T - расстояние(2.68), численно равное длине волны, которое плоская волна преодолеваетс фазовой v скоростью за промежуток времени, численно равный T периоду гармонических колебаний И источника этой плоской волной.

Величина (2.69) Ф₁ = ω(t - y/ v )+ φ₀ = ωt - ky+ φ₀ равна фазовому углу, который имеют частицы упругой среды, находящиеся на y расстоянии от И источника гармонических колебаний, при своём отклонении от положения равновесия в данный момент t времени. Эта Ф₁ величина называется фазой волны, распространяющейся в положительном (рис. 02.0.17)направлении OY оси. Вдоль отрицательного (рис. 02.0.17)направления OY оси в момент t₁ = T/4 времени частицы упругой среды, находящиеся на y = λ/4 расстоянии от И источника гармонических колебаний в Пл. 3 плоскости равных фаз будут иметь отклонение от положения равновесия, равное A амплитуде, но в противоположную сторону по сравнению с отклонениямичастиц упругой среды в Пл. 2 плоскости равных фаз положительного направления OY оси. Источник И гармонических колебаний фаз в момент t₁ = T/4 времени будет иметь (рис. 02.0.2) фазовый угол, равный π/2, а частицы упругой среды в Пл. 3 плоскости равных фаз будут находиться в фазе π, опережающей фазовый угол этого источника на угол π/2. Поэтому при распространении волны вдоль отрицательного (рис. 02.0.17)направления OY оси величина (2.69) ky, зависящая от расстояния Пл. 3 плоскости равных фаз колебаний частиц до И источника, будет определять опережение Ф₂ фазы волны по сравнению с ωt + φ₀ фазой гармонических колебаний И источника. Фаза Ф₂ волны в случае её распространения в отрицательном (рис.2.17)направления OY оси в произвольный момент t времени будет иметь следующий вид: Ф₂ = ωt + ky+ φ₀. (2.71) Уравнение распространяющейся в отрицательную сторону OY оси плоской синусоидальной волны, т.е. s=s(t) зависимость отклонения от положения равновесия частиц упругой среды в произвольный момент t времени, распространяющейся вдоль отрицательного направления OY оси, по аналогии с (2.69) и с учётом (2.70) будет иметь следующий вид: s = A cos(ωt + ky+ φ₀), (2.72) где y – имеет положительное численное значение и равняется расстоянию от 0 начала координат по OY оси до волнового фронта плоской синусоидальной волны, распространяющейся вдоль отрицательного направления OY оси в произвольный момент t времени. Фазы Ф₁ (2.69) и Ф₂ (2.71) упругих волн величиныпостоянные при распространении соответственно в положительном и отрицательном направлениях по OY оси в плоскости равных фаз. Поэтому для волнового фронта плоской синусоидальной волны зависимость Ф₁ фазы (2.69) и Ф₂ (2.71)этой волны от y координаты колеблющихся частиц упругой среды, начальной φ₀ (2.70) фазы колебаний частиц упругой среды имеет следующий вид: Ф_{2 , 1} = ωt ± ky + φ₀ = const. (2.73) где знаки "+", "-" указывают на распространение плоской синусоидальной волны в упругой среде соответственно в отрицательном и положительном направлениях по OY оси. Возьмём первую производную по t времени от левой и правой частей (2.74) выражения вследствие чего выражение для определения фазовой v скорости имеет следующий вид:

dФ_{2 , 1} /dt = d(ωt)/dt ± d(ky)/dt + d(φ₀)/dt ↔ 0 = ω ± kdy/dt = 0 ↔ dy/dt = ± ω/k. (2.74) С учётом равенства первой производной от y координаты волнового фронта плоской синусоидальной волны по t времени фазовой v скорости перемещенияэтого волнового фронта в направлении (рис. 02.0.17) k волнового вектора,т.е. dy/dt= v, выражение (2.74) принимает следующий вид:v = ± ω/k, (2.75) где ω - циклическая частота гармонических колебаний (рис.2.16) И источника, вследствие чего в упругой среде возникаетволна; k - волновое число, равное k модулю k волнового вектора, направленного (рис. 02.0.17) по OY оси, тогда в правой части (2.76) выражения ставится "+" знак, и направленного (рис. 02.0.17) противоположно OY оси, тогда в правой части (2.76) выражения ставится

Date: 2015-06-11; view: 281; Нарушение авторских прав