
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Вращающийся Aвектор, равный сумме векторов A1 иA2 , изображающих соответственногармонические колебания1 - го грузикаотносительно 2- го грузикаи гармонические колебания 1 page
|
|
2 грузика вместе с 1 грузиком относительно O началакоординат в произвольный момент
t времени, т.е. A = A 1 + A2, изображает результирующее колебание 1 грузика относительно O начала координат.
Фазы колебаний 1 - го (2.14) и 2- го (2.15) грузиков на рис.2.5 в данный момент t времени обозначены соответственно Ф1 и Ф2, а фаза Ф результирующего колебания 1 - го грузика относительно O начала координат обозначена Ф. В произвольный момент времени Ф1 и Ф2 фазы колебаний 1 - го (2.14) и 2- го (2.15) грузиков имеют следующий вид:
Ф1 = ω1 t+ φ1; Ф2 = ω2 t+ φ2. (2.16)
|

координат; z - результирующая координата 1 - го грузика, т.е. отклонение от положения равновесия 1 - го грузика в зависимости от t времени, когда учитываются его (2.11) z1 колебания на а пружине в системе координат, связанной со 2 - ым грузиком, а также учитываются его (2.12) z2 колебания на b пружине как единое целое со 2 - ым грузиком относительно O начала координат.
По теореме косинусов A модуль результирующего вектора A (рис. 02.0.5)на векторной диаграмме имеет следующий вид:
A = {A 1 2 + A 2 2 - 2A 1 A 2 cos [π -(Ф 2 -Ф1)]} 1/2 =[A 1 2 + A 2 2 + 2A 1 A 2 cos (Ф 2 -Ф1)] 1/2. (2.18)
В выражении (2.18) Ф2 - Ф1 является разностью Ф2 фазы гармонических колебаний 2- го грузика вместе с 1 - ым грузиком относительно O начала координат в произвольный момент
t времени и Ф1 фазы гармонических колебаний 1 - го грузика относительно 2- го грузика.
Фаза Ф результирующего вектора A (рис.2.5)на векторной диаграмме результирующего по OZ оси колебания 1 - го грузика относительно O начала координат в (2.14) выраженииимеет следующий вид: tgФ = (A1 sinФ1+ A2 sinФ2)/(A1cosФ1+ A2cosФ2) ↔ ↔ Ф = arctg[(A1 sinФ1+ A2 sinФ2)/(A1cosФ1+ A2cosФ2)]. (2.19) Два z1 и z2 гармонических колебания называются когерентными, если Ф2 - Ф1 разность их фаз не зависит от t времени и имеет следующий вид: Ф2 - Ф1 = (ω2 - ω1)t + (φ2 - φ1) = const (2.20) Выполнение условия (2.20) возможно, если ω2 = ω1 = ω. Тогда Ф2 - Ф1 разность фаз когерентных колебаний равна следующей φ2 - φ1 разности их начальных фаз: Ф2 - Ф1 = φ2 - φ1 = φ0 . (2.21) При выполнении (2.21) условия результирующее (2.17) z колебание двух складываемых
z1 и z2 гармонических колебаний одного направления является тоже гармоническим с той же циклической ω частотой, что и эти складываемые колебания, вследствие чего z результирующее колебание двух складываемых z1 и z2 гармонических колебаний имеет следующий вид: z = z1 + z2 = Acos(ωt + φ0). (2.22) Выражение для A амплитуды результирующего колебания как суммы двух когерентных колебаний получается подстановкой (2.21) Ф2 - Ф1 = φ2 - φ1 разности фаз когерентных колебаний в (2.18), вследствие чего получается следующее выражение: A = [A 1 2 + A 2 2 + 2A 1 A 2 cos(φ2 - φ1)]1/2, (2.23)
Выражение(2.19) начальной Ф0 фазы результирующего колебания как суммы двух когерентных колебаний получается подстановкой в (2.13) начального t0 времени, равного нулю, т.е. t0 = 0, вследствие чего получается следующее выражение для начальной Ф0 фазы результирующего колебания: Ф10 = φ1; Ф20 = φ2 ↔ tgФ0 = (A1 sinφ1+ A2 sin φ2)/(A1cos φ1 + A2cos φ2) ↔ ↔ Ф0 = arctg[(A1sinφ1+ A2 sinφ2)/(A1cosφ1+ A2cosφ2)], (2.24) где (2.14) A1 , φ1, рад - соответственно амплитуда и начальная фаза приколебаниях 1 - го грузика на a пружине относительно 2- го грузика; (2.15) A2 , φ2, рад - соответственно амплитуда и начальная фаза приколебаниях 1 - го грузика на b пружине как единое целое со 2 - ым грузиком относительно O начала координат.
В зависимости от значения φ2 - φ1 = φ0 разности начальных фаз складываемых колебаний
A амплитуда результирующего колебания согласно выражению (2.23) изменяется в следующих пределах: от A = | A 1 - A 2 | при φ 2 - φ 1 = ±(2m + 1)π (2.25) до A = A 1 + A 2 при φ 2 - φ 1 = ±2mπ, (2.26) где m = 0,1,2,… - любое целое неотрицательное число.
Если (2.26) φ2 - φ1 = φ0 = ±2mπ, т.е. разность начальных фаз складываемых когерентных колебаний кратна 2π, то говорят, что складываемые колебания физической величины синфазны. В случае сложения синфазных механических, электромагнитных или электромеханических колебаний A амплитуда результирующего колебания складываемых физических величин максимальна.
Если (2.25) φ2 - φ1 = φ0 = ±(2m + 1)π, т.е. разность начальных фаз складываемых когерентных колебаний кратна нечётному числу π, то говорят, что складываемые колебания физической величины противофазны. В случае сложения противофазных механических, электромагнитных или электромеханических колебаний A амплитуда результирующего колебания складываемых физических величин минимальна.
Результирующие колебания двух складываемых (2.17) гармонических колебаний одного направления, циклические (2.2) частоты ω1 и ω2 колебаний которых различны, т.е. ω2 ≠ ω1, являются некогерентными колебаниями, т.к. разность их фаз Ф = Ф2 - Ф1 = (ω2 - ω1)t + (φ2 - φ1) непрерывно изменяется с течением t времени. При сложении таких колебаний получаются негармонические результирующие колебания. Негармонические колебания, получающиеся в результате сложения двух одинаково направленных гармонических колебаний с близкими ω1, ω2 (2.14), (2.15) циклическими частотами,т.е. | ω2 - ω1 | << ω1, называются биениями.
Сложение взаимно перпендикулярных гармонических колебаний равных и кратных частот.
Пусть материальная M точка одновременно колеблется вдоль OY и OZ осей координат в соответствии со следующими уравнениями:
y = A1cos(ωt + φ1); z = A2 cos(ωt + φ2), (2.27) где y, z - координата материальной M точки в зависимости от t времени при колебаниях соответственно вдоль OY и OZ осей координат; ω - циклическая частота(2.2) гармонических колебаний материальной M точки, одинаковая по OY и OZ осям координат; A1 , φ1, рад - соответственно амплитуда и начальная фаза приколебаниях материальной M точки по OY оси;
A2 , φ2, рад - соответственно амплитуда и начальная фаза приколебаниях материальной M точки по OZ оси.
|
OYZ плоскости можно найти, выразив из (2.24) уравнения z = A2 cos(ωt+ φ2) колебания материальной M точки по OZ оси параметр ωt =[arcos(y/A2)] - φ2, подставив этот параметр ωt в уравнение y = A1 cos(ωt+ φ1) колебания материальной M точки по OY оси. Исключив таким образом из уравнений (2.27) t времени, получаем следующее уравнение Т траекториирезультирующего движения материальной M точки в OYZ плоскости: (y2/A12) + (z2/A22) - (2yz/ A1A2)cos(φ2 - φ1) = sin2(φ2 - φ1). (2.28)
На OYZ плоскости (2.28) уравнение Т траектории результирующего движения материальной M точки представляет собой эллипс с A1 и A2 полуосями, равными (2.27) A1 и A2 амплитудам складываемых взаимно перпендикулярных гармонических колебаний этой материальной M точки.
|

являющегося Т траекторией (рис. 02.0.6) результирующего движения материальной M точки в
OYZ плоскости, совпадают с OY и OZ осями координат, а размеры полуосей этого эллипса равны
A1 и A2 амплитудам складываемых (2.24) взаимно перпендикулярных гармонических колебаний материальной M точки.
Уравнение Т траектории результирующего движения материальной M точки (2.28) в этом случае примет следующий вид: (y2/A12) + (z2/A22) = 1. (2.29) Материальная M точка, колеблющаяся вдоль взаимно перпендикулярных направлений с одинаковой циклической (2.2) ω частотой, совершает один полный оборот по Т траектории,представляющийсобой(рис. 02.0.6) эллипс,за время, равное T = 2π/ω периоду складываемых колебаний.
Если A1 и A2 амплитуды складываемых (2.27) взаимно перпендикулярных гармонических колебаний материальной M точки равны друг другу, т.е. A1 = A2, то Т траектория (2.29) результирующего движения материальной M точки представляет собой окружность. В тех случаях, когда φ2 - φ1 разность начальных фаз складываемых колебаний кратна π, т.е. φ2 - φ1 = ±mπ, где m = 0, 1, 2,…, n, то Т траектория (2.28) результирующего движения материальной M точкииз эллипса вырождается в отрезок прямой, вследствие чего уравнение Т траектории этого результирующего движения материальной M точки примет следующий вид: z = ± (A1/ A2)y. (2.30) Знак " +" в выражении (2.30) соответствует сложению взаимно перпендикулярных гармонических колебаний, когда эти колебания синфазны, а знак "-" соответствует сложению противофазных колебаний.
|
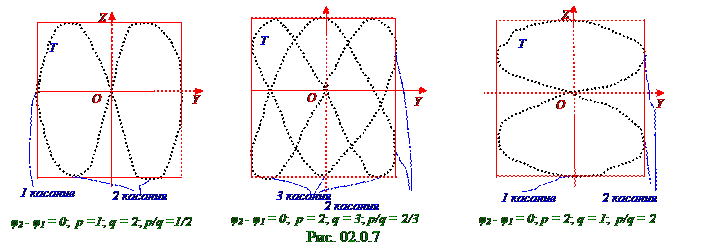
Сложение взаимно перпендикулярных гармонических колебаний с циклическими частотами pω и qω, где p и q - целые числа: y= A1 cos(pωt+ φ1); z = A2 cos(qω t+ φ2), где p и q - целые числа, приводит к движению материальной M точки по траектории, названной фигурой Лиссажу. На рис. 02.0.7 приведены различные случаи Т траекторий движения материальной M точки, колеблющейся во взаимно перпендикулярных направлениях с указанными соотношениями циклических pω и qω частот.
Отношение частот pω и qω складываемых колебаний равно отношению числа касаний соответствующей им фигуры Лиссажу со стороной прямоугольника, параллельной OZ оси, и со стороной, параллельной OY оси.
Лекция 5. Динамика гармонических колебаний. Энергия и импульс гармонического осциллятора. Фазовая траектория колебательной системы. Физический маятник. Квазиупругая сила колебательной системы. Дифференциальное уравнение свободных затухающих колебаний и его решение. Декремент и логарифмический декремент свободных затухающих колебаний. Добротность колебательной системы. Дифференциальное уравнение вынужденных колебаний и его решение. Механический резонанс колебательных процессов
Динамика гармонических колебаний. Энергия и импульс гармонического осциллятора.
У некоторых механических систем потенциальная Wp энергия является функцией одной переменной. Если у такой механической системы существует устойчивое положение равновесия, в котором потенциальная Wp энергия этой механической системы имеет минимум, а полная WΣ энергия, т.е. сумма кинетической Wk и потенциальной Wp энергии, величина постоянная, т.е. не зависят от t времени, то такую механическую систему называют гармоническим осциллятором.
В гармоническим осцилляторе материальная точка m массой совершает свободные незатухающие колебания под действием упругой или квазиупругой силы.
|

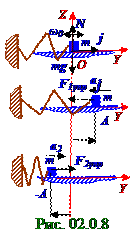
маятника заменена равной этой Δy проекции величиной y координаты, отсчитанной от O начала координат, которое находится в точке устойчивого равновесия пружинного маятника.
В (2.31) применено равенство m(d2y/dt2) = Fупрy потому, что по OY оси на материальную точку m массой действует единственная сила, которой является (рис. 02.0.8) сила упругости пружины, вектор Fупр (1.40)из раздела 01.0 " Физические основы механики " которой является равнодействующим
вектором силы, приложенным к материальной точке. Приложенные по OZ оси к материальной точке m массой вектора m g силы тяжести и N силы реакции опоры уравновешивают друг друга. Если пружинный (рис. 02.0.8) маятник растянут, т.е. y1 координата материальной точки m массой больше нуля, то векторы a1 ускорения и F 1 упр силы упругости коллинеарны j единичному вектору (1.1) из раздела 01.0.0 " Физические основы механики " и направлены противоположно этому j единичному вектору.
Если пружинный (рис. 02.0.8) маятник сжат, т.е. y2 координата материальной точки m массой меньше нуля, то векторы a2 ускорения и F 2 упр силы упругости коллинеарны j единичному вектору (1.1) из раздела 01.0.0 " Физические основы механики " и направлены в одну сторону с этим j единичным вектором.
По аналогии с (1.97) – (1.107) из раздела 01.0 " Физические основы механики " и с
учётом (2.31) определяем Wp потенциальную энергию материальной точки m массой при её отклонении (2.28) на величину y = s(t) = A cos(ωt+ φ0) относительно равновесия под воздействием упругой силы Fупрy в заданный момент t времени из следующего выражения:
Wp y
dWp = - Fупрydy ↔ dWp = mω02ydy ↔ Wp = ∫dWp = ∫mω0 2ydy = (mω0 2y2)/2 = 0 0
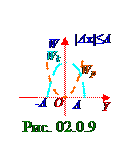
= (mω02A2/2)cos2(ω0t+ φ0) = (mω02A2/4)[1+ cos(2ω0t+2φ0)]. (2.32) Согласно (2.32) Wp потенциальная энергия, графическая зависимость которой на рис. 02.0.9 от величины отклонения Δy пружинного маятника относительно положения равновесия изображена короткими пунктирными линиями оранжевого цвета, минимальна в точке устойчивого равновесия
|
пружинного маятника, совпадающей с O началом координат.
При максимальном отклонении пружинного маятникаотположения равновесия, когда модуль | Δ y| вектора Δ y смещения равен амплитуде колебаний этого пружинного маятника, т.е. | Δ y| = y = A, потенциальная Wp энергия согласно (2.33) становитсяравной (mω0 2A2)/2. Потенциальная Wp энергия (2.32) пружинного маятника изменяется с циклической 2ω0 (2.2) частотой в 2 раза превышающей ω0 циклическую частоту прямолинейных гармонических колебаний (рис. 02.0.8) материальной точки m массой.
Кинетическая Wk энергия (1.88) из раздела 01.0.0 " Физические основы механики " материальной точки m массой, совершающей прямолинейные гармонические колебания по OY оси с учетом (2.9) ds/dt = dx/dt = v = - Aωsin(ωt+ φ0) скорости смещения этойматериальной точки m массой в произвольный момент t времени имеет следующий вид: Wk = m v 2/2 = = (mω02A2/2) sin2(ω0t+ φ0) = (mω02A2/4)[1 - cos(2ω0 t+2φ0)] = = (mω02A2/2)[1 - cos2(ω0t + φ0)] = (mω02/2)(A2 - x2). (2.33) Согласно (2.33) Wk кинетическая энергия, графическая зависимость которой на рис.2.9 от величины отклонения Δy пружинного маятника относительно положения равновесия изображена длинными пунктирными линиями бирюзового цвета, максимальна в точке устойчивого равновесия этого пружинного маятника, совпадающей с O началом координат.При максимальном отклонении пружинного маятникаотположения равновесия, когда модуль | Δ y| вектора Δ y смещения равен амплитуде колебаний этого пружинного маятника, т.е. | Δ y| = y = A, кинетическая Wk энергия согласно (2.33) становитсяравной нулю.
Date: 2015-06-11; view: 375; Нарушение авторских прав