
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Комбинации триграмм и стихий
|
|
Триграммный порядок Фуси традиционно связывается с фразой из “Си цы чжуани” (I, 11), в которой говорится о дихотомическом делении Великого предела. Однако в этом тексте указывается только сам принцип образования триграмм, а не его конкретное воплощение, в действительности могущее иметь несколько вариантов. Таким образом, если порядок Фуси — не единственный порядок триграмм, который можно построить по принципу дихотомии, то следует предположить, что, во-первых, должны были быть какие-то основания для его выбора среди других порядков, а во-вторых, эти другие тоже могли как-то применяться в арифмосемиотике.
Как указывалось ранее (см. гл. 1.2), порядок Фуси строится посредством разбиения позиций триграмм на полярности, которое осуществляется в последовательности снизу вверх, от Земли к Небу (рис. 2.2.1, ср. рис. 1.2.10—12; читается справа налево).

Рис. 2.2.1
Однако разбиение позиций на полярности возможно и в других последовательностях. Например, при прохождении позиций сверху вниз, от Неба к Земле, получится порядок триграмм, являющийся зеркальным отражением порядка Фуси (рис. 2.2.2). В обоих случаях позиционное формирование триграмм имеет своим истоком Великий предел. Но в первом случае триграммы как бы “стоят” на нем, а во втором — “висят” под ним.

Рис. 2.2.2
Помимо различия в направлении построения позиций (сверху вниз или снизу вверх) существуют еще различия в исходной позиции (1-я, 2-я или 3-я). Таким образом, чередуя последовательность прохождения позиций, можно получить в общей сложности шесть порядков триграмм, которые образуют две серии (А и В), зеркальные друг другу (табл. 2.2.1).
| Таблица 2.2.1 | |||||
| Серия A | Серия B | ||||
| A3 | A2 | A1 | B3 | B2 | B1 |
| Поз. 3-2-1 | Поз. 1-3-2 | Поз. 2-1-3 | Поз. 3-1-2 | Поз. 2-3-1 | Поз. 1-2-3 |
| 111 — М | 111 — М | 111 — М | 111 — М | 111 — М | 111 — М |
| 110 — Д | 011 — М | 101 — О | 101 — О | 110 — Д | 011 — М |
| 101 — О | 110 — Д | 011 — М | 110 — Д | 011 — М | 101 — О |
| 100 — П | 010 — В | 001 — Д* | 100 — П | 010 — В | 001 — Д* |
| 011 — М | 101 — О | 110 — Д | 011 — М | 101 — О | 110 — Д |
| 010 — В | 001 — Д* | 100 — П | 001 — Д* | 100 — П | 010 — В |
| 001 — Д* | 100 — П | 010 — В | 010 — В | 001 — Д* | 100 — П |
| 000 — П | 000 — П | 000 — П | 000 — П | 000 — П | 000 — П |
Из этих шести порядков только один непосредственно зафиксирован в традиции — порядок Фуси (В1). Остальные же присутствуют в ней латентно и могут быть выявлены через различные связи триграмм с другими символически-смысловыми комплексами арифмосемиотики, прежде всего, со стихиями и с пневмами- ци. Все эти связи требуют тщательного анализа.
В табл. 2.2.1 также приведена корреляция триграмм и стихий: Цянь и Дуй — металл; Кунь и Гэнь — почва; Сюнь и Чжэнь — дерево (по связям с этими триграммами будем условно различать “первичное” и “вторичное” дерево — Д и Д*); Кань — вода; Ли — огонь. В синологии не установлено время возникновения данной корреляции. Известно, что она встречается в сохранившихся письменных источниках, относящихся к сунской эпохе. Так, например, эта корреляция приводится в сочинении неоконфуцианца Шао Юна (1011—1077) “Мэй хуа и шу” (“Числа перемен цветов сливы”) (см.: Числа 1993: 23). Несмотря на такую позднюю датировку, можно с уверенностью сказать, что происхождение данной корреляции триграмм и стихий значительно более раннее, поскольку в ней отражены основные закономерности арифмосемиотики, в частности, закономерности оперирования со стихиями, известные с доханьского времени.
В “Си цы чжуани” говорится:
Высокое — подражание (сяо) Небу.
Низкое — способ (фа) [действия] Земли.
Небо и Земля устанавливаются по позициям (вэй).
Перемены (и) движутся (син) между ними (Си цы, I, 5).
На основании данной фразы можно сделать вывод, что “старшие” триграммы Цянь и Кунь, имеющие в качестве природных манифестаций (образов) Небо и Землю, выступают в качестве неких полюсов, между которыми происходят преобразования, описываемые шестью “младшими” триграммами. Порядки этих шести триграмм можно сопоставить с пятеричными порядками стихий, которые также были призваны описывать различные трансформации. Примечательно, что движение, о котором говорится в “Си цы чжуани”, выражается тем же иероглифом, что и понятие “стихия” — син.
Еще одна цитата из “Си цы чжуани”:
Цянь и Кунь — это тайные силы (юнь) перемен (и).
Цянь и Кунь разделились, и перемены установились между ними.
Если разрушить Цянь и Кунь, то не будут проявляться перемены.
Если не будут проявляться перемены, то Цянь и Кунь совсем истощатся (Си цы, I, 12).
В этом пассаже Цянь и Кунь представлены не просто границами, между которыми совершаются перемены, а одновременно и источниками силы, приводящими в действие перемены, и получателями неких энергий, исходящих от проявлений перемен.
Таким образом, модель субъект-объектного взаимодействия, рассмотренную ранее (гл. 2.1), можно применить для интерпретации триграмм в новом качестве — соотнося развертку этого взаимодействия, подразделяемого на прямое и обратное действия, не с позициями триграмм, а с наборами “младших” триграмм, в той или иной комбинации выстраивающихся между “старшими” Цянь и Кунь, которые, подобно субъекту и объекту, находятся вне самих этих действий.
Данный подход позволяет вдобавок уточнить функциональное значение корреляций “старших” триграмм со стихиями. Такие корреляции должны отражать не сходство триграмм и стихий, а “место” подключения “старших” триграмм к набору “младших”; они просто фиксируют стихию прилегающей триграммы. Поэтому эти корреляции должны быть различными, устанавливаемыми в зависимости от порядка стихий. Однако в китайской традиции имеется представление только о вышеуказанном варианте корреляций (других либо не было вовсе, либо они забылись), и правомерен он только для триграммных порядков А2, B1 и производных от них.
О семантической связи “младших” триграмм и стихий свидетельствует сходство природных манифестаций (образов) некоторых из триграмм с коррелирующими с ними стихиями (табл. 2.2.2).
| Таблица 2.2.2 | ||||
| Код | Название | Образ | Свойство образа | Стихия |
| Цянь | Небо | господствует (цзюнь) | металл | |
| Дуй | Водоем | благодарит (шо) | металл | |
| Ли | Солнце (Огонь) | согревает (сюань) | огонь | |
| Чжэнь | Гром (Молния) | возбуждает (дун) | дерево* | |
| Сюнь | Ветер, Дерево | распределяет (сань) | дерево | |
| Кань | Дождь (Вода) | смачивает (жунь) | вода | |
| Гэнь | Гора | сдерживает (чжи) | почва | |
| Кунь | Земля | хранит (цан) | почва |
Это образы: Огонь (101), Вода (010) и Дерево (110). Правда, в качестве коррелята триграммы Сюнь образ Дерева менее употребим, чем Ветер, но о связи данной триграммы со стихией “дерево” намекает еще традиционная корреляция последней с пневмой “ветер” в списке пяти пневм (у ци) (табл. 2.2.3).
| Таблица 2.2.3 | ||||
| Дерево | Огонь | Почва | Металл | Вода |
| ветер (фэн) | тепло (шу) | влажность (ши) | сухость (цзао) | холод (хань) |
Образы триграмм Дуй и Гэнь, возможно, были взаимно переставлены, поскольку для стихии “почва”, которую в арифмосемиотике связывали с пневмой “влажность”, а Дун Чжушу в “Чуньцю фань-лу” (“Обильная роса на летописи “Чуньцю””) назвал “сыростью Неба” (Дун чжушу 1990: 126), более уместна связь с Водоемом (Болотом, Низиной — цзэ), а для металла, который коррелирует с пневмой “сухость” и ассоциировался с горами, где он, вероятно, когда-то добывался, более уместна связь с образом Горы. К тому же по корреляциям, опосредованным стихиями, триграммы Дуй (металл) и Гэнь (почва) связаны соответственно с западом и центром Китая, где расположены горы и низменность.
Можно также предположить, что первоначально вместо дерева с триграммой Чжэнь, образ которой — Гром (Молния), а одно из значений — “забеременеть”, коррелировала какая-то другая стихия, “громо-молние-подобная” или “семенная”, “жизнепроизводящая”, поскольку, по реконструкции, на этом месте в одних случаях (в схеме суточной циркуляции пневмы- ци по меридианам) стоит вторичный огонь (О*) — “огонь-министр” (сян хо), а в других (в “Цзо чжуани”) — “зерно” (цзя). Последнее более вероятно, поскольку, во-первых, не требует повторов стихий (Д-Д* или О-О*), а во-вторых, делает их список более содержательным. Зерно — это потенция жизни, динамическая “живая стихия” (тут можно провести параллели с “живым веществом” В.И. Вернадского) среди других стихий, жизнь принимающих и поддерживающих. Стихия “дерево”, если оттенить ее понимание в качестве простого материала (древесины), также обладает некой степенью “жизненности”, что и позволило, по всей видимости, при упрощении теории поставить ее на место зерна.
Схемы циклов
Для более удобного анализа древнекитайских мироописательных схем с арифмосемиотической символикой (триграммы, стихии, пневмы, циклические знаки и т.д.) в дальнейшем будет использоваться специальная схема описания — “базис-схема”, представляющая собой круг (символ циклически развивающихся процессов), который имеет несколько вариантов членения — простое двенадцатеричное членение, с объединением двенадцати частей круга по парам и шестеричное, при котором более дробные величины не существенны (рис. 2.2.3; северные циклические знаки здесь размещаются по китайскому образцу — внизу схемы).
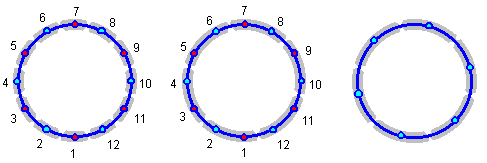
Рис. 2.2.3
Если расположить порядки триграмм А-серии на базис-схеме, связав “младшие” триграммы с ее шестью элементами, то можно увидеть, что они преобразуются один в другой за счет сдвига триграмм по некоей внутренней фигуре, причем порядки триграмм размещаются как в по часовой стрелке, так и против нее (рис. 2.2.4).

Рис. 2.2.4
Эта внутренняя фигура, которая далее будет называться “гексанемой” (гр. hex шесть + nema нить), интересна тем, что она не только часто встречается в тех или иных подвергшихся реконструкции древнекитайских арифмосемиотических схемах, отражая их инвариантные закономерности, но и является компонентом “эннеаграммы” (от гр. ennea — 9), предъявленной Г.И. Гюрджиевым (иное написание — Гурджиев; 1877—1949) на его лекциях в Европе и Америке и опубликованной, в частности, его последователем П.Д. Успенским в середине прошлого века (см.: Успенский 1999: 384, 393). По сведениям Г.И. Гюрджиева, схема эннеаграммы применялась в древнем мире для записи тайных знаний. К сожалению, более определенно о ее истоках он не высказывался. Однако на основании нижеприводимого комплекса исследований можно предположить, что эта схема в некоей своей первоначальной форме, отдельные стороны которой проступают в арифмосемиотике, была создана в Китае в западночжоускую эпоху. Можно также предположить, что со временем эннеаграмма проникла на Запад, где чудом сохранилась в одном из эзотерических учений, из которого и была заимствована Г.И. Гюрджиевым.
В самых общих чертах эннеаграмма представляет собой круг, на котором размещен ряд натуральных чисел от 1 до 9 (рис. 2.2.5). Эти числа играют в данной схеме роль специфической символики явлений, происходящих в определенных целостных образованиях, и подразделяются на два набора. Числа 1, 2, 4, 5, 7, 8 связаны друг с другом внутри круга линиями (которые и составляют гексанему) в следующем порядке: 1, 4, 2, 8, 5, 7... Остальные три числа — 3, 6, 9 — образуют треугольник. Набор из шести чисел в двух указанных порядках символизирует некие циркуляции “энергий” внутри взятых для символизирования целостностей, а троичный набор обозначает силы, приводящие в действие эти самые “энергии”.

Рис. 2.2.5
Гексанема является наиболее характерной деталью эннеаграммы. Она задается циклической дробью 1/7 = 0,[142857]. Следует отметить, что аналогичная циклическая последовательность образуется при делении на 7 любого целого числа (если, конечно, оно не кратно числу 7). При другом числителе начало периода просто сместится (например, 3/7 = 0,[428571]). Однако для получения данного периода необходимо, чтобы деление производилось в десятеричном счислении, и неизвестно, использовалось ли оно при создании эннеаграммы. С другой стороны, составляющую этот период последовательность чисел можно получить при делении на 7 круга, который при этом делится еще на десять частей, каждая из которых также делится на десять частей, делимых, в свою очередь, на десять частей и т.д. (рис. 2.2.6). Такое построение кажется более правдоподобным, учитывая общий уровень знаний в древности, но в этом случае “эннеаграмму” вернее было бы называть “декаграммой” (от гр. deka — 10).

Рис. 2.2.6
Следует отметить, что гексанему можно получить посредством деления круга на 7 не только в системе счисления с основанием 10. Основанием системы счисления, в которой образуется гексанема, является любое число n = (13 +7i)/2, если i = 1, 3, 5, 7..., или n = (10 + 7i)/2, если i = 2, 4, 6, 8... Например, если i = 2, то n = 12.
Деление круга на двенадцать частей используется в календаре и поэтому является особо интересным. При построении гексанемы на двенадцатеричном основании круг сначала делится на 12 частей, они также делятся на 12 частей и так до бесконечности. При последующем делении круга на 7 частей их величины можно будет выразить с любой точностью с помощью образовавшейся двенадцатеричной шкалы. Далее следует соединить линиями цифры, входящие в периодическую дробь 12/7 = 1,[8|6|10|3|5|1] и обозначающие либо границы соответствующих частей, получаемых при делении круга на 12, либо сами эти части (рис. 2.2.7). Образовавшуюся схему следует назвать “додекаграммой” (от гр. d` odeka — 12). Конкретным ее выражением в китайской арифмосемиотике может быть схема года, которая подразделялась китайцами как на 12 месяцев по 29 или 30 дней, так и на 28 периодов по числу лунных стоянок сю (см. табл. 1.5.3; рис. 1.5.1), которые можно разбить на 7 групп с 4-мя сю в каждой.

Рис. 2.2.7
Если не брать во внимание различия в символике, ракурс схемы и некоторые не отмеченные здесь несущественные подробности, то следует признать, что гексанема в гюрджиевской эннеаграмме, в реконструированных декаграмме и додекаграмме и гексанема, образуемая на круге “младших” триграмм, достаточно схожи по строению и функциям.
Триграммы можно представить в виде чисел от 0 до 7, и тогда сходство эннеаграммы и триграммных схем будет еще большим. Для этого надо поставить в соответствие янским знакам в позициях триграмм X, Y, Z числа 4, 2, 1, суммы которых в каждой триграмме определят соответствующее ей число (табл. 2.2.4).
| Таблица 2.2.4 | ||||||||
| X Y Z | ||||||||
| S |
Несмотря на то, что шестеричная базис-схема с триграммами призвана иллюстрировать преобразования порядков шести “младших триграмм”, в ней латентно заложено представление о семеричности. “Старшие” триграммы, начинающие и заканчивающие эти порядки, можно рассматривать как смыкающиеся, и тогда все триграммы обозначат семь частей, на которые делится круг базис-схемы (рис. 2.2.8). Смычка Кунь / Цянь, не участвующая в преобразованиях, будет соответствовать тому лучу семилучевой звезды, с которого начинается деление. “Младшие” триграммы в соответствии со своими численными выражениями будут коррелировать с остальными лучами. Эти оставшиеся лучи попадают в зоны, на которые подразделяется круг при его шестеричном делении. Поэтому условно можно считать, что гексанема связывает именно эти шесть зон, а не пункты разбивки круга на семь частей.

Рис. 2.2.8
“Младшие” триграммы, выстраивающиеся по гексанеме на рассмотренных базис-схемах, образуют следующий замкнутый порядок: 100—110—010—011—001—101 (см. рис. 2.2.4, 2.2.8, ср. рис. 2.1.4). Его характерной особенностью является то, что он последовательно связывает триграммы, имеющие только одну позицию с различающимися знаками. В современной информатике связи двоичных кодов по принципу изменения знака только в одной позиции считаются наиболее энергетически выгодными, а сама операция по преобразованию кода подобным образом называется “шагом Хемминга”. Надо отметить, что для шести “младших” триграмм возможна только одна подобная связь, зафиксированная как раз в гексанеме. Образующийся на основе этой связи порядок триграмм далее будет называться “ротационным” или “ротатором” (R), исходя из того, что одной из его функций является участие в циклических сдвигах при преобразованиях других порядков триграмм.
Порядки триграмм В-серии также преобразуются друг в друга посредством сдвигов “ротатора” по гексанеме, но только этот сдвиг осуществляется в противоположном направлении (рис. 2.2.9).

Рис. 2.2.9
Перекодировка триграмм В-серии в числа должна иметь обратную корреляцию чисел 1, 2, 4 с позициями триграмм (табл. 2.2.5).
| Таблица 2.2.5 | ||||||||
| X Y Z | ||||||||
| S |
В-серия, в которой находится порядок Фуси (В1), не включает в себя известные порядки стихий, представленные в корреляции с “младшими” триграммами (см. табл. 2.2.1). Эта серия проявляет себя в закономерностях взаимодействий шести пневм- ци,коррелирующих с триграммами (см. следующую главу). Напротив, в А-серии имеется два важнейших порядка стихий — “взаимопорождение” (А3) и “взаимопреодоление” (А1). Для удобства далее соответствующие порядки триграмм будут именоваться аналогично.
То, что при корреляции стихий с шестью “младшими” триграммами образуются также шестеричные порядки стихий, вовсе не мешает соотнести последние с пятеричными. Стихии коррелируют с триграммами так, что две “младшие” триграммы (001 и 110) оказываются связанными с деревом. Однако в рассматриваемых порядках триграмм они стоят рядом и при этом взаимодействуют одновременно по принципам “взаимопорождения” и “взаимопреодоления”, которые нейтрализуют друг друга, приводя к уменьшению различий между взаимодействующими триграммами. Поэтому эти триграммы и могут быть связаны с одной стихией, а шестеричный порядок стихий может быть преобразован в пятеричный. При таком преобразовании получится классическая пентаграмма, в которой по кругу стихии располагаются в порядке “взаимопорождения”, а по звезде — в порядке “взаимопреодоления” (рис. 2.2.10; ср. рис. 1.3.4).

Рис. 2.2.10
Таким образом, в учении о стихиях зафиксированы частные закономерности взаимодействия триграмм. По всей видимости, пятеричный набор стихий в порядке “взаимопорождения” может отражать тот же самый процесс развития неких реалий, что и триграммный порядок А3, но только с учетом запаздывания. Если началом процесса полагать стихию “дерево”, а полные периоды развития пятеричного и шестеричного наборов стихий принять одинаковыми по времени, то получится, что каждая другая стихия доходит до кульминации своего развития в пятеричном порядке несколько позже, чем в шестеричном. С другой стороны, если считать фазы развития отдельных стихий в шестеричном и пятеричном наборах одинаковыми, пятеричный цикл будет заканчиваться раньше, чем шестеричный, и новый пятеричный цикл также будет начинаться раньше предыдущего со сдвигом на одну стихию, как это происходит в китайском календаре (ср. табл. 1.5.4—6).
Такое свойство шестеричного порядка обусловлено, видимо, тем, что он, выделенный из целостной системы триграмм, мыслится сам по себе, без соотнесения с другими порядками, которые через множество взаимосвязей могут препятствовать или способствовать как его развитию в целом, так и смыканию триграмм 001 и 110, коррелирующих с одной и той же стихией. Кроме того, рассматривая шестеричный порядок в контексте восьмеричного набора триграмм, следует учитывать, что триграмма Цянь обозначает некий источник энергии, который осуществляет подпитку процесса, символизируемого “младшими” триграммами. Пятеричный же набор стихий, согласно традиционной теории, не имеет дополнительного источника энергии, поэтому символизируемый им процесс затухает быстрее.
Аналогичные рассуждения справедливы и для порядков В1 и В3, которые имеют структурные отношения, подобные отношениям порядков А3 и А1.
Фазы развития
Известно, что четверка стихий “дерево”, “огонь”, “металл”, “вода”, представляющая собой фрагмент порядка “взаимопорождения”, обозначает четыре фазы развития растений в годовом цикле: рождение, рост, созревание, увядание (см. рис. 1.3.1). Стихия “почва”, помещаемая между огнем и металлом, обозначает приостановку роста и переход к процессу созревания (см. рис. 1.3.3). Коррелирующие с этими стихиями триграммы символизируют те же самые фазы развития, но рассматриваемые с позиции небесно-земных отношений.
Как ни странно, забытый китайцами триграммный шестеричный порядок “взаимопорождения” является по сравнению с пятеричным порядком стихий не только более удобным для описания временных циклов по правилам, принятым в древнем Китае, но и более согласующимся с этими правилами по структуре. Так, китайцы подразделяли год на две половины — янскую (“весна” — чунь) и иньскую (“осень” — цю) — и на шесть 60- или 59-дневных периодов. Подобную структуру задают верхняя и начальная черты триграмм в порядке А3 (рис. 2.2.11).

Рис. 2.2.11
Следует отметить, что триграммные порядки можно рассматривать как дискретное описание сцепки трех колебательных процессов, в которых периоды колебаний определяются расположением триграмм. Так, в случае полного, восьмитриграммного порядка “взаимопорождения”, который задается верхней позицией, описывающей колебательный процесс с некоторым заданным периодом, нижестоящие позиции будут символизировать колебательные процессы, имеющие периоды в 2 и 4 раза меньшие, а при сокращении этого порядка до шести “младших” триграмм все эти колебательные процессы можно рассматривать находящимися в отношении 1, 1/2 и 1/3 (рис. 2.2.12). При этом в шестеричном порядке “взаимопорождения” средний колебательный процесс приобретет несколько смещенную форму. Если попытаться “выправить” его ритм, то сместится ритм в первой позиции триграмм. Вероятно, имеет смысл говорить о каком-то их обоюдном динамическом урегулировании, значительно усложняющем всю ритмическую триграммную конструкцию и выводящем ее за пределы банальной модели сложения трех синусоидальных колебаний. С другой стороны, надо учитывать, что произведенное здесь сокращение “старших” триграмм является упрощением, и при анализе любого шестеричного цикла, построенного на “младших” триграммах, следует подразумевать, что за ним стоят Цянь и Кунь, которые играют роль его инициаторов, обладающих некими специфическими формами колебаний и энергий.

Рис. 2.2.12
Благодаря незримому присутствию “небесной энергии” “старшей” триграммы Цянь, процесс годового развития, описываемый шестеричным триграммным циклом, начинается с небесного “одаривания” (110) растений живительными силами, потом происходит “процветание” (101) и “сдерживание” (100) этого “процветания” в момент его кульминации. На этом заканчивается первый полупериод развития. Затем наступает пора “благодарения” (011) — созревание растений, сбор урожая и подношения Небу. После этого природа вступает в фазу “упадка” (010), когда важно сохранить урожай. Здесь исчерпывается аналогия в символизации фаз развития посредством стихий и триграмм, но порядок триграмм еще не заканчивается. После фазы упадка вступает в действие триграмма Чжэнь (001), значение которой связано с понятием “возбуждение”. В системе стихий символ этой фазы отсутствует, но в отношении циклов взаимодействия сил ян и инь как таковых китайцы держались мнения, что в конце каждого полуцикла наступает парадоксальная фаза, являющаяся “зародышем” нового полуцикла. Это символизируется черной и светлой точками на противоположных по цвету частях монады Тай цзи (см. рис. 2.2.11). В данном случае такими “зародышами” будут триграммы Гэнь (100) и Чжэнь (001). Поэтому “возбуждение”, связанное с последней “младшей” триграммой, — это то, что приводит к появлению нового рождения, символизируемого следующей по кругу триграммой Сюнь (110) из другого триграммного цикла, который дополнительно подкрепляется связанной с ним триграммой Цянь. С другой стороны, энергия триграммы Чжэнь уходит еще в следующую за ней “старшую” Кунь, так же как и Цянь, незримо управляющую годовым шестеричным циклом.
Процесс развития триграмм в порядке “взаимопорождения” происходит по позициям сверху вниз, поэтому тотальная активность в этом порядке связана с верхней, субъектной позицией (табл. 2.2.6; ср. с табл. 2.1.7). Это главным образом означает, что активность нижней позиции в триграммах Дуй (011) и Чжэнь (001) несколько меньшая по сравнению с той, что могла бы быть при отсутствии тотальной активности — именно к такому случаю относились вышеприведенные (см. гл. 2.1) интерпретации названий триграмм и их свойств. Таким образом, объектное действие имеет меньшую возможность достигнуть верхней позиции. Поэтому янский знак (1) в нижней позиции данных триграмм указывает в большей степени на оформленность (результативность) действия высших сил, чем на противодействие им, будь оно подкреплением или подавлением.
| Таблица 2.2.6 | ||||||||
| Локальная активность | ® | ® | ® | ® | — | — | ||
| Порядок “взаимопорождения” | ||||||||
| Тотальная активность | ® | ® | ® | ® | ® | ® | ® | ® |
При условном исключении “старших” триграмм из порядка “взаимопорождения” он разделится на два полупериода, в которых будут доминировать соответственно действия субъекта и объекта (см. табл. 2.2.6). В случае с порядком Фуси субъектные и объектные действия поменяются местами (см. табл. 2.1.7). Если эти действия рассматривать в динамике, то можно снова прийти к колебательной модели. Таким образом, зеркальные триграммные порядки “взаимопорождения” (А3) и Фуси (В1) будут интерпретироваться как описания любых циклических процессов развития, стимулируемых соответственно “небесной” (субъект) и “земной” (объект) энергиями. При этом основная позиция триграмм в этих порядках — та, с которой начинается дихотомическое деление (для А3 — верхняя, а для В1 — нижняя), — будет символизировать периоды подъема и спада процесса развития (рис. 2.2.13), а остальные позиции — более мелкие фазы, придающие ему специфичность (на рис. 2.2.13 не указаны). Баланс активности субъекта и объекта, вынесенных из самого процесса, будет находиться в обратной зависимости по отношению к этим периодам подъема и спада: при развитии процесса, символизируемого порядком “взаимопорождения”, будет угасать активность субъекта и латентно возрастать активность объекта, а при спаде — наоборот; полностью зеркальной будет ситуация с порядком Фуси; в обоих случаях имеется субъект-объектная уравновешенность в центрах фаз с триграммами Ли (101) и Кань (010).
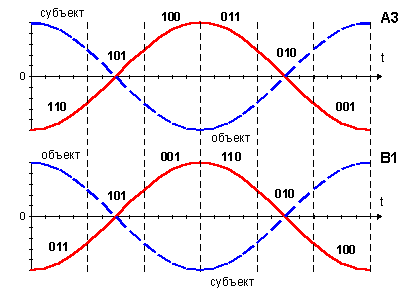
Рис. 2.2.13
Для каждого из этих порядков триграммы Ли (101) и Кань (010) обозначают наиболее характерные фазы полупериодов — соответственно “процветание” и “упадок”; триграммы Сюнь (110) и Дуй (011) символизируют начала полупериодов — “одаривание” и “подношение”; триграммы Чжэнь (001) и Гэнь (100) символизируют окончание полупериодов, их кульминацию — “возбуждение, движение” и “сдерживание, покой”. В порядке В1 последние триграммы находятся соответственно в янском и иньском полупериодах, что согласуется с их свойствами, т.к. движение- дун — это янский принцип, а покой- цзин — иньский. В порядке А3 эти триграммы находятся в противоположных им по знаку полупериодах, что ведет к инверсности их свойств — иньское “движение” является теперь “покоем”, а янский “покой” — “движением”.
Остальные порядки, взятые из набора порядков триграмм, которые получаются путем простого дихотомического деления (см. табл. 2.2.1), занимают в каждой серии подчиненное положение по отношению к порядкам А3 и В1, определяемое по позиции триграмм, с которой начинается деление. Вместе все эти порядки образуют сложную конструкцию субъект-объектного взаимодействия:
Небо — А3¯ В3
Человек — А2¯ В2
Земля — А1¯ В1
“ Космогонический” и “современный” порядки
Два из четырех наиболее известных в китайской традиции порядков стихий — “взаимопорождение” и “взаимопреодоление” — выводятся, как было показано выше, из триграммных порядков А3 и А1. Оставшиеся “космогонический” и “современный” порядки также можно построить на основе их корреляций с триграммами. Для этого надо особым способом, который можно условно обозначить как “симметрично-дихотомическое” деление, преобразовать порядки А3 (“взаимопорождение”) и В1 (Фуси), точнее, только выделенные из них порядки “младших” триграмм. В принципе, все порядки серий А и В могут быть преобразованы этим способом, образуя две производные серии С и D (табл. 2.2.7, ср. табл. 2.2.1), в которых, возможно, найдутся еще какие-нибудь корреляты второстепенных традиционных порядков стихий. Однако для простоты изложения следует ограничиться рассмотрением преобразований А3 и В1 в C3 и D1. Именно последние два порядка задают структуру коррелирующих с ними “космогонического” и “современного” порядков стихий. Эти триграммные порядки далее будут именоваться аналогично.
| Таблица 2.2.7 | |||||
| Серия A | Серия B | ||||
| A3 | A2 | A1 | B3 | B2 | B1 |
| Серия C | Серия D | ||||
| C3 | C2 | C1 | D3 | D2 | D1 |
| 110 — Д | 011 — М | 101 — О | 101 — О | 110 — Д | 011 — М |
| 001 — Д* | 100 — П | 010 — В | 010 — В | 001 — Д* | 100 — П |
| 101 — О | 110 — Д | 011 — М | 110 — Д | 011 — М | 101 — О |
| 010 — В | 001 — Д* | 100 — П | 001 — Д* | 100 — П | 010 — В |
| 100 — П | 010 — В | 001 — Д* | 100 — П | 010 — В | 001 — Д* |
| 011 — М | 101 — О | 110 — Д | 011 — М | 101 — О | 110 — Д |
Метод “симметрично-дихотомического” деления основывается на том, что полупериоды подъема и спада как порядка А3, так и В1 симметричны подобно половинкам круга или полупериодам косинусоиды (см. рис. 2.2.13). Эти полупериоды делятся на три фазы, символизируемые соответственно тремя триграммами. Но их можно разделить на шесть фаз, связанных со всеми шестью “младшими” триграммами, половина из которых проецируется в каждый полупериод из противоположного полупериода. В дальнейшем данные полупериоды можно рассматривать как самостоятельные циклы, несущие в себе тенденции только подъема или только спада, что определяется направлением порядка триграмм.
Триграммный порядок А3 (“взаимопорождение”) после подобного преобразования трансформируется в “космогонический” порядок (рис. 2.2.14). Классический “космогонический” порядок стихий является пятеричным и начинается с воды: В, О, Д, М, П. Получившийся порядок шестеричен, но триграммы Сюнь и Чжэнь, коррелирующие с деревом, стоят в нем рядом, и поэтому эта стихия не разделяется на два вида. Данный порядок начинается с дерева или металла, в зависимости от направления чтения (обратный “космогонический” — Д, Д*, О, В, П, М или прямой “космогонический” — М, П, В, О, Д*, Д). Подобно порядку “взаимопорождения”, его можно рассматривать замкнутым, кольцевым. При расположении “космогонического” порядка на круге исходный для него порядок “взаимопорождения” образует фигуру гексанемы.
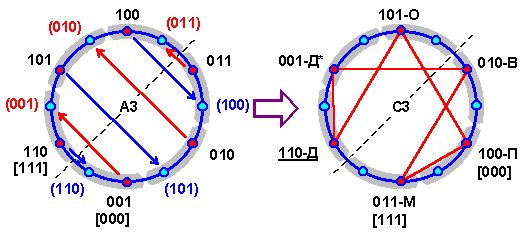
Рис. 2.2.14
“Современный” порядок (М, Д, В, О, П) просматривается в преобразовании порядка Фуси (В1) (рис. 2.2.15). Здесь также дерево не разделяется, а полученный порядок может прочитываться в различных направлениях: обратный “современный” — М, П, О, В, Д*, Д и прямой “современный” — Д, Д*, В, О, П, М. При круговом расположении “современного” порядка исходный для него порядок Фуси образует, как и в предыдущем случае, фигуру гексанемы.

Рис. 2.2.15
Полученные порядки стихий — “космогонический” (С3) и “современный” (В1) — различаются между собой местоположениями огня и воды. Главным же их отличием от “классических” вариантов является не то, что они начинаются с иных элементов — в кольцевой структуре это оказывается несущественным, а то, что в них имеется дополнительная связь с триграммами Цянь и Кунь, благодаря которой они обретают новые функциональные характеристики.
Таким образом, четыре порядка стихий, наиболее известные в китайской традиции, основываются на системе триграмм. Эта система обладает более высокой степенью организованности, чем набор стихий. В учении о триграммах содержится дополнительная информация, придающая ему большую логичность и концептуальную подкрепленность по сравнению с учением о стихиях. Рассмотрение последнего учения сквозь призму знаний о триграммах делает его более понятным. Традиционно триграммам приписывается более раннее происхождение, чем учению о стихиях. Учитывая вышесказанное, можно сделать вывод, что учение о стихиях является упрощением более древнего учения о триграммах.
“Ротатор”
Стержневым порядком триграмм в этом учении является “ротационный” (R): 100—110—010—011—001—101. Он не только необходимым образом присутствует в преобразованиях порядков А-, B-, C- и D-серии, но и может служить источником для получения всех рассматривавшихся здесь порядков. Если расположить его на базис-схеме, а затем с учетом различных осей симметрии выстраивать новые порядки по принципу “симметрично-дихотомического” деления, то на первом этапе получатся все порядки А- и В-серии, а на втором — C- и D-серии.
При всех этих преобразованиях важно правильно выбирать ракурс исходной схемы и совершать развертку новообразованных порядков на базис-схеме. Так, чтобы получить порядок A1 (“взаимопреодоление”), необходимо выбрать такой ракурс базис-схемы с “ротатором”, при котором можно было бы начать развертку с правой ее части и с триграммы 110 (рис. 2.2.16; данная триграмма выделена подчеркиванием).

Рис. 2.2.16
Для получения порядков А3 (“взаимопорождение”) и В1 (Фуси) необходимо выбрать другие ракурсы базис-схемы с “ротатором”, и хотя развертка новообразованного порядка здесь также производится с правой части схемы, но начинается она с той же триграммы 110 только во втором случае, а для первого берется триграмма 011 (рис. 2.2.17). Аналогичным образом варьируются условия получения всех остальных порядков А- и В-серии.

Рис. 2.2.17
Чтобы получить из триграммных порядков А3 и В1 соответственно “космогонический” (C3) и “современный” (D1), необходимо осуществить их развертку уже с левой части базис-схемы, от триграмм 110 и 011 (рис. 2.2.18).

Рис. 2.2.18
В принципе, можно не останавливаться на этом шаге и продолжать преобразования, чередуя начальные условия развертки новообразуемых порядков. Правда, открытий каких-либо дополнительных аналогов древнекитайским порядкам триграмм при этом ожидать не следует. Во всяком случае, сохранившиеся в китайской культуре порядки триграмм с получаемыми таким образом новыми порядками не сопоставимы. Но это и не важно. Значение данной процедуры заключается в другом: на шестом ее шаге образуется исходный порядок.
Если преобразования начинаются с какого-либо порядка (например, А3 или В1), то на шестом шаге произойдет возвращение к нему же, но находящемуся в ином масштабе времени, — ведь при каждом преобразовании происходило деление исходного порядка на две части. Если длительность некоего процесса, описываемого исходной триграммной схемой, принимается за единицу, то после полного шестеричного цикла преобразований получится такая же последовательность триграмм, что и в исходной схеме, но развертка данной последовательности будет осуществляться за время, меньшее в 64 раза по сравнению с исходной последовательностью. Иными словами, исходная последовательность триграмм складывается из 64-х себе подобных последовательностей. Но это только часть общей картины, поскольку исходная последовательность триграмм складывается еще из 2-х, 4-х, 8-ми, 16-ти и 32-х последовательностей триграмм, которые получаются из нее в промежуточных преобразованиях. Таким образом, порядки триграмм по своей сути являются сложноорганизованными структурами с масштабированным самоподобием содержащихся в них временных ритмов.
Такое масштабированное самоподобие в современной науке называется “фрактальным”, а получаемые сходным способом схемы — “фракталами”. Наука о фракталах еще очень молода, и многое в ней пока не обрело окончательной формы. Первоначально в качестве фракталов исследовались разнообразные геометрические фигуры. Однако в дальнейшем стало ясно, что фрактальная методология более универсальна. Например, в качестве фракталов стали пониматься некоторые сложные коммуникативные схемы. С помощью фрактальной методологии ученые также пытаются подойти к исследованию времени, тем самым наводя мосты с древнекитайской арифмосемиотикой.
Date: 2016-08-30; view: 439; Нарушение авторских прав